 Đề thi toán 9, đề kiểm tra toán 9 kết nối tri thức có đáp án và lời giải chi tiết
Đề thi toán 9, đề kiểm tra toán 9 kết nối tri thức có đáp án và lời giải chi tiết
 Đề khảo sát chất lượng đầu năm Toán 9 - Kết nối tri thức
Đề khảo sát chất lượng đầu năm Toán 9 - Kết nối tri thức Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
Bài 1 (1,0 điểm): 1. Biểu đồ cột kép biểu diễn diện tích gieo trồng sắn của tỉnh Bình Thuận (cũ) và tỉnh Bình Phước (cũ) trong các năm 2018; 2019; 2020 (đơn vị: Nghìn ha).
Đề bài
Bài 1 (1,0 điểm):
1. Biểu đồ cột kép biểu diễn diện tích gieo trồng sắn của tỉnh Bình Thuận (cũ) và tỉnh Bình Phước (cũ) trong các năm 2018; 2019; 2020 (đơn vị: Nghìn ha).
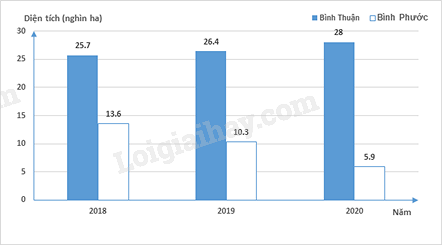
Tính tỉ số phần trăm diện tích trồng sắn của Bình Phước so với Bình Thuận vào năm 2020 (làm tròn đến chữ số thập phân thứ hai).
2. Một túi đựng bút tô màu của bạn Bình có 4 chiếc bút màu đỏ, 6 chiếc bút màu cam, 5 chiếc bút màu xanh và 3 chiếc bút màu tím (các chiếc bút có cùng khối lượng và kích thước). Bạn Bình lấy ngẫu nhiên một chiếc bút từ trong túi. Tính xác suất của các biến cố sau: "Lấy được chiếc bút màu đỏ hoặc màu cam".
Bài 2 (2,0 điểm): Cho biểu thức: \(A = \frac{{{x^2} - 1}}{{1 - 2x}}\) và \(B = \frac{2}{{x + 1}} - \frac{1}{{x - 1}} - \frac{{5 - x}}{{1 - {x^2}}}{\rm{\;}}\left( {x \ne \frac{1}{2},x \ne \pm 1} \right)\)
a) Tính giá trị của A biết \({\rm{x}} = 2\)
b) Rút gọn biểu thức B
c) Tìm \(x\) nguyên để A.B có giá trị nguyên.
Bài 3 (3,0 điểm):
1. Giải các phương trình sau:
a) \(\frac{{x - 2}}{4} + \frac{{2x - 3}}{3} = \frac{{x - 18}}{6}\)
b) \(5x\left( {x + 3} \right) = 9 - {x^2}\)
2. Giải bài toán bằng cách lập phương trình:
Lúc 8 giờ một người đi xe máy khởi hành từ A với vận tốc 40km/giờ. Sau đó 30 phút, một người đi ô tô từ A đuổi theo với vận tốc 60km/giờ. Hỏi đến mấy giờ người đi ô tô mới đuổi kịp người đi xe máy và nơi gặp nhau cách A bao nhiêu km?
Bài 4 (3,5 điểm): Cho \(\Delta {\rm{ABC}}\) nhọn \(({\rm{AB}} < {\rm{AC}})\), ba đường cao AE, BD, CF cắt nhau tại H
a) Chứng minh \(\Delta {\rm{ABD}}\) đồng dạng \(\Delta {\rm{ACF}}\).
b) Chứng minh \(\Delta {\rm{ABC}}\) đồng dạng \(\Delta {\rm{ADF}}\) và \({\rm{BH}}.{\rm{BD}} + {\rm{CH}}.{\rm{CF}} = {\rm{B}}{{\rm{C}}^2}\).
c) Chứng minh \(\frac{{HE}}{{AE}} + \frac{{HD}}{{BD}} + \frac{{HF}}{{CF}} = 1\).
Bài 5 (0,5 điểm): Có 5 vận động viên thi đấu cờ vua theo thể thức vòng tròn một lượt.
a) Hỏi có bao nhiêu trận đấu diễn ra.
b) Biết vận động viên hạng 1 không có trận nào hòa, hạng 2 không có trận nào thua và hạng 4 không có trận nào thắng. Hỏi điểm số của các vận động viên sau khi thi đấu là bao nhiêu, biết nếu thắng thì được 1 điểm, hòa được 0,5 điểm, thua 0 điểm và các vận động viên không bằng điểm với nhau.
---HẾT----
Lời giải
Bài 1 (1,0 điểm):
1. Biểu đồ cột kép biểu diễn diện tích gieo trồng sắn của tỉnh Bình Thuận (cũ) và tỉnh Bình Phước (cũ) trong các năm 2018; 2019; 2020 (đơn vị: Nghìn ha).
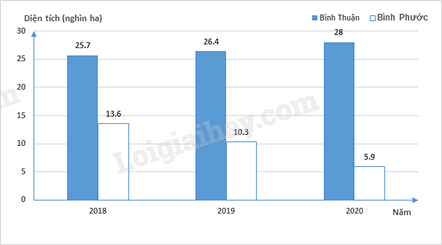
Tính tỉ số phần trăm diện tích trồng sắn của Bình Phước so với Bình Thuận vào năm 2020 (làm tròn đến chữ số thập phân thứ hai).
2. Một túi đựng bút tô màu của bạn Bình có 4 chiếc bút màu đỏ, 6 chiếc bút màu cam, 5 chiếc bút màu xanh và 3 chiếc bút màu tím (các chiếc bút có cùng khối lượng và kích thước). Bạn Bình lấy ngẫu nhiên một chiếc bút từ trong túi. Tính xác suất của các biến cố sau: "Lấy được chiếc bút màu đỏ hoặc màu cam".
Phương pháp:
1. Xác định diện tích trồng sắn của Bình Phước và Bình Thuận vào năm 2020 rồi tính tỉ số phần trăm:
Tỉ số phần trăm = BP : BT . 100%.
2. Xác định số kết quả có thể khi lấy ngẫu nhiên một chiếc bút từ trong túi.
Xác định số kết quả thuận lợi cho biến cố: "Lấy được chiếc bút màu đỏ hoặc màu cam".
Lời giải:
1. Quan sát biểu đồ ta thấy năm 2020:
- Diện tích trồng sắn của Bình Phước là 5,9 (ha)
- Diện tích trồng sắn của Bình Thuận là 28 (ha)
Vậy tỉ số phần trăm diện tích trồng sắn của Bình Phước so với Bình Thuận vào năm 2020 là:
\(\frac{{5,9}}{{28}}.100\% \approx 21,07\% \).
2. Vì túi đựng có 4 chiếc bút màu đỏ, 6 chiếc bút màu cam, 5 chiếc bút màu xanh và 3 chiếc bút màu tím nên số kết quả có thể khi lấy ngẫu nhiên một chiếc bút từ trong túi là: 4 + 6 + 5 + 3 = 18.
Có 4 chiếc bút màu đỏ, 6 chiếc bút màu cam nên số kết quả thuận lợi cho biến cố lấy được chiếc bút màu đỏ hoặc màu cam là: 4 + 6 = 10
Vậy xác suất của biến cố "Lấy được chiếc bút màu đỏ hoặc màu cam" là: \(\frac{{10}}{{18}} = \frac{5}{9}\)
Bài 2 (2,0 điểm): Cho biểu thức: \(A = \frac{{{x^2} - 1}}{{1 - 2x}}\) và \(B = \frac{2}{{x + 1}} - \frac{1}{{x - 1}} - \frac{{5 - x}}{{1 - {x^2}}}{\rm{\;}}\left( {x \ne \frac{1}{2},x \ne \pm 1} \right)\)
a) Tính giá trị của A biết \({\rm{x}} = 2\)
b) Rút gọn biểu thức B
c) Tìm \(x\) nguyên để A.B có giá trị nguyên.
Phương pháp:
a) Thay \(x = 2\) (nếu thoả mãn điều kiện) vào A để tính giá trị.
b) Sử dụng quy tắc trừ phân thức khác mẫu để rút gọn biểu thức.
c) Tính A.B.
Ta có: \(A.B = \frac{m}{{g\left( x \right)}}\) trong đó h(x) là một biểu thức nguyên khi x nguyên, m nguyên.
Biện luận A.B nguyên khi \(\frac{m}{{g\left( x \right)}}\) nguyên, suy ra \(g\left( x \right) \in \)Ư(m).
Kết hợp điều kiện ban đầu của \(x\) để kết luận.
Lời giải:
a) Thay \(x = 2\) (TMĐK \(x \ne \frac{1}{2},x \ne \pm 1\)) vào A, ta được:
\(A = \frac{{{2^2} - 1}}{{1 - 2.2}} = \frac{{4 - 1}}{{1 - 4}} = \frac{3}{{ - 3}} = - 1\)
Vậy \(A = - 1\) khi \(x = 2\)
b) Ta có:
\(B = \frac{2}{{x + 1}} - \frac{1}{{x - 1}} - \frac{{5 - x}}{{1 - {x^2}}}{\rm{\;}}\left( {x \ne \frac{1}{2},x \ne \pm 1} \right)\)
\(\begin{array}{l}B = \frac{2}{{x + 1}} - \frac{1}{{x - 1}} - \frac{{x - 5}}{{{x^2} - 1}}\\B = \frac{{2\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \frac{{x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \frac{{x - 5}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\B = \frac{{2x - 2 - x - 1 - x + 5}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\B = \frac{2}{{{x^2} - 1}}\end{array}\)
Vậy \(B = \frac{2}{{{x^2} - 1}}\)
c) \(A.B = \frac{{{x^2} - 1}}{{1 - 2x}}.\frac{2}{{{x^2} - 1}} = \frac{2}{{1 - 2x}}\)
Để A.B nguyên thì \(\frac{2}{{1 - 2x}}\) nguyên hay \(\left( {1 - 2x} \right) \in \)Ư(2) = \(\left\{ { - 2; - 1;1;2} \right\}\).
Ta có bảng giá trị sau:

Kết hợp với điều kiện ban đầu \(x \ne \frac{1}{2},x \ne \pm 1\), ta được \(x = 0\)
Vậy \(x = 0\) thì \(A.B\) nguyên.
Bài 3 (3,0 điểm):
1. Giải các phương trình sau:
a) \(\frac{{x - 2}}{4} + \frac{{2x - 3}}{3} = \frac{{x - 18}}{6}\)
b) \(5x\left( {x + 3} \right) = 9 - {x^2}\)
2. Giải bài toán bằng cách lập phương trình:
Lúc 8 giờ một người đi xe máy khởi hành từ A với vận tốc 40km/giờ. Sau đó 30 phút, một người đi ô tô từ A đuổi theo với vận tốc 60km/giờ. Hỏi đến mấy giờ người đi ô tô mới đuổi kịp người đi xe máy và nơi gặp nhau cách A bao nhiêu km?
Phương pháp:
1.
a) Đưa phương trình về phương trình bậc nhất một ẩn để giải.
b) Chuyển vế phải sang vế trái, sử dụng phân tích đa thức thành nhân tử để biến đổi vế trái.
Giải phương trình A.B = 0 thì A = 0 hoặc B = 0.
2. Đổi thời gian về cùng đơn vị.
Gọi thời gian người đi xe máy đi là \(x\) (giờ), đặt điều kiện của x theo đề bài.
Biểu diễn được thời gian, quãng đường xe máy và ô tô đi.
Vì hai người cùng khởi hành từ A nên quãng đường ô tô và xe máy đi được là bằng nhau, ta lập được phương trình.
Đưa phương trình về phương trình bậc nhất một ẩn và giải.
Kiểm tra điều kiện và kết luận.
Tính thời điểm ô tô đuổi kịp xe máy và khoảng cách từ A tới điểm gặp nhau.
Lời giải:
1. a) \(\frac{{x - 2}}{4} + \frac{{2x - 3}}{3} = \frac{{x - 18}}{6}\)
\(\begin{array}{l}\frac{{3\left( {x - 2} \right)}}{{4.3}} + \frac{{4\left( {2x - 3} \right)}}{{4.3}} = \frac{{2\left( {x - 18} \right)}}{{6.2}}\\3\left( {x - 2} \right) + 4\left( {2x - 3} \right) = 2\left( {x - 18} \right)\\3x - 6 + 8x - 12 = 2x - 36\\3x + 8x - 2x = - 36 + 6 + 12\\9x = - 18\\x = - 2\end{array}\)
Vậy \(x = - 2\).
b) \(5x\left( {x + 3} \right) = 9 - {x^2}\)
\(\begin{array}{l}5{x^2} + 15x = 9 - {x^2}\\5{x^2} + {x^2} + 15x - 9 = 0\\6{x^2} + 15x - 9 = 0\\2{x^2} + 5x - 3 = 0\\2{x^2} - x + 6x - 3 = 0\\x\left( {2x - 1} \right) + 3\left( {2x - 1} \right) = 0\\\left( {x + 3} \right)\left( {2x - 1} \right) = 0\end{array}\)
TH1: \(x + 3 = 0\) suy ra \(x = - 3\).
TH2: \(2x - 1 = 0\) suy ra \(x = \frac{1}{2}\).
Vậy \(x \in \left\{ { - 3;\frac{1}{2}} \right\}\).
2. Đổi 30 phút = \(\frac{1}{2}\) giờ.
Gọi thời gian người đi xe máy đi là \(x\) (giờ), \(x > \frac{1}{2}\).
Khi đó thời gian người đi ô tô đi là: \(x - \frac{1}{2}\) (giờ).
Quãng đường người đi xe máy đi được là: \(40x\) (km).
Quãng đường người đi ô tô đi được là: \(60\left( {x - \frac{1}{2}} \right)\) (km).
Vì hai người cùng khởi hành từ A nên quãng đường ô tô và xe máy đi được là bằng nhau, ta có phương trình:
\(\begin{array}{l}60\left( {x - \frac{1}{2}} \right) = 40x\\60x - 30 = 40x\\60x - 40x = 30\\20x = 30\end{array}\)
\(x = \frac{3}{2}\) (giờ) = 1 giờ 30 phút
Vậy hai người gặp nhau lúc 8 giờ + 1 giờ 30 phút = 9 giờ 30 phút.
Nơi gặp nhau cách A là: \(40.\frac{3}{2} = 60\) km.
Bài 4 (3,5 điểm): Cho \(\Delta {\rm{ABC}}\) nhọn \(({\rm{AB}} < {\rm{AC}})\), ba đường cao AE, BD, CF cắt nhau tại H
a) Chứng minh \(\Delta {\rm{ABD}}\) đồng dạng \(\Delta {\rm{ACF}}\).
b) Chứng minh \(\Delta {\rm{ABC}}\) đồng dạng \(\Delta {\rm{ADF}}\) và \({\rm{BH}}.{\rm{BD}} + {\rm{CH}}.{\rm{CF}} = {\rm{B}}{{\rm{C}}^2}\).
c) Chứng minh \(\frac{{HE}}{{AE}} + \frac{{HD}}{{BD}} + \frac{{HF}}{{CF}} = 1\).
Phương pháp:
a) Chứng minh $\Delta ABD\backsim \Delta ACF\left( g.g \right)$.
b) Chứng minh $\Delta ABC\backsim \Delta ADF$ (c.g.c)
Chứng minh $\Delta BHE\backsim \Delta BCD$ (g.g), suy ra $BH.BD=BE.BC$
Chứng minh $\Delta CHE\backsim \Delta CBF$ (g.g), suy ra $CH.CF=CE.CB$
Suy ra \({\rm{BH}}.{\rm{BD}} + {\rm{CH}}.{\rm{CF}} = {\rm{B}}{{\rm{C}}^2}\).
c) Nhân cả tử và mẫu của \(\frac{{HE}}{{AE}}\) với \(\frac{1}{2}BC\).
Nhân cả tử và mẫu của \(\frac{{HD}}{{BD}}\) với \(\frac{1}{2}AC\).
Nhân cả tử và mẫu của \(\frac{{HF}}{{CF}}\) với \(\frac{1}{2}AB\).
Xuất hiện diện tích các tam giác tương ứng, từ đó chứng minh tổng của chúng bằng 1.
Lời giải:
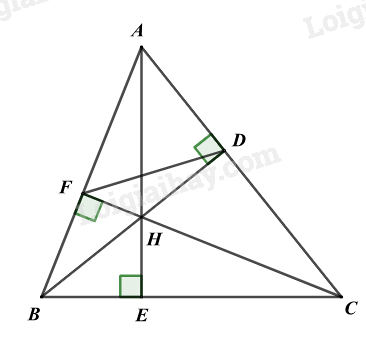
a) Chứng minh $\Delta ABD\backsim \Delta ACF$
Xét \(\Delta ABD\) và \(\Delta ACF\) có:
\(\widehat D = \widehat F\left( { = 90^\circ } \right)\) (vì BD và CF là đường cao)
\(\widehat A\) chung
Vậy $\Delta ABD\backsim \Delta ACF\left( g.g \right)$.
b) Chứng minh $\Delta ABC\backsim \Delta ADF$
Vì $\Delta ABD\backsim \Delta ACF$ nên \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AF}}\) hay \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AF}}\).
Xét \(\Delta ABC\) và \(\Delta ADF\) có:
\(\frac{{AB}}{{AD}} = \frac{{AC}}{{AF}}\) (cmt)
\(\widehat A\) chung
Vậy $\Delta ABC\backsim \Delta ADF$ (c.g.c)
Chứng minh \(BH.BD + CH.CF = B{C^2}\)
Xét \(\Delta BHE\) và \(\Delta BCD\) có:
\(\widehat B\) chung
\(\widehat {BEH} = \widehat {BDC}\left( { = 90^\circ } \right)\) (vì AE và BD là đường cao)
Do đó $\Delta BHE\backsim \Delta BCD$ (g.g), suy ra \(\frac{{BH}}{{BC}} = \frac{{BE}}{{BD}}\) nên \(BH.BD = BE.BC\) (1)
Chứng minh tương tự ta có $\Delta CHE\backsim \Delta CBF$ (g.g), suy ra \(\frac{{CH}}{{CB}} = \frac{{CE}}{{CF}}\) nên \(CH.CF = CE.CB\) (2)
Từ (1) và (2) suy ra:
\(BH.BD + CH.CF = BE.BC + CE.CB = \left( {BE + CE} \right).BC = BC.BC = B{C^2}\)
c) Chứng minh \(\frac{{HE}}{{AE}} + \frac{{HD}}{{BD}} + \frac{{HF}}{{CF}} = 1\)
\(\begin{array}{l}\frac{{HE}}{{AE}} + \frac{{HD}}{{BD}} + \frac{{HF}}{{CF}}\\ = \frac{{\frac{1}{2}HE.BC}}{{\frac{1}{2}AE.BC}} + \frac{{\frac{1}{2}HD.AC}}{{\frac{1}{2}BD.AC}} + \frac{{\frac{1}{2}HF.AB}}{{\frac{1}{2}CF.AB}}\\ = \frac{{{S_{\Delta HBC}}}}{{{S_{\Delta ABC}}}} + \frac{{{S_{\Delta HAC}}}}{{{S_{\Delta BAC}}}} + \frac{{{S_{\Delta HAB}}}}{{{S_{\Delta CAB}}}}\\ = \frac{{{S_{\Delta HBC}} + {S_{\Delta HAC}} + {S_{\Delta HAB}}}}{{{S_{\Delta ABC}}}}\\ = \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta ABC}}}} = 1\end{array}\)
Bài 5 (0,5 điểm): Có 5 vận động viên thi đấu cờ vua theo thể thức vòng tròn một lượt.
a) Hỏi có bao nhiêu trận đấu diễn ra.
b) Biết vận động viên hạng 1 không có trận nào hòa, hạng 2 không có trận nào thua và hạng 4 không có trận nào thắng. Hỏi điểm số của các vận động viên sau khi thi đấu là bao nhiêu, biết nếu thắng thì được 1 điểm, hòa được 0,5 điểm, thua 0 điểm và các vận động viên không bằng điểm với nhau.
Phương pháp:
a) Đánh số thứ tự 5 vận động viên, liệt kê các trận đấu diễn ra: mỗi vận động viên đấu với 4 vận động viên còn lại.
b) Dựa vào các thông tin: vận động viên hạng 1 không có trận nào hòa, hạng 2 không có trận nào thua và hạng 4 không có trận nào thắng và các vận động viên không bằng điểm với nhau để xác định số trận thắng, hoà, thua của từng thứ hạng.
Từ đó xác định số điểm của từng thứ hạng.
Lời giải:
a) Ta đánh số thứ tự 5 vận động viên lần lượt là 1, 2, 3, 4, 5.
Vì mỗi vận động viên đấu với 4 vận động viên còn lại nên ta có các trận đấu diễn ra là:
1 – 2, 1 – 3, 1 – 4, 1 – 5, 2 – 3, 2 – 4, 2 – 5, 3 – 4, 3 – 5, 4 – 5.
Vậy có 10 trận đấu diễn ra.
b) Giả sử vận động viên hạng 1 có số thứ tự là 1; vận động viên hạng 2 có số thứ tự là 2; vận động viên hạng 3 có số thứ tự là 3; vận động viên hạng 4 có số thứ tự là 4; vận động viên hạng 5 có số thứ tự là 5.
Theo bài ra thì mỗi vận động viên thi đấu 4 trận.
Vì vận động viên hạng 1 không có trận nào hoà và hạng 2 không có trận nào thua nên trận đấu 1 – 2 thì hạng 2 thắng. Do đó số điểm hạng 1 đạt được có thể là:
+) 3 điểm (thắng 3 trận, thua 1 trận).
+) 0 điểm (thua 4 trận).
Mà vận động viên hạng 2 không có trận nào thua nên các trận còn lại thắng hoặc hoà. Do đó số điểm hạng 2 đạt được có thể là:
+ Thắng 1 trận, hoà 3 trận: 1 + 3.0,5 = 2,5 điểm
+ Thắng 2 trận, hoà 2 trận: 2.1 + 2.0,5 = 3 điểm
+ Thắng 3 trận, hoà 1 trận: 3.1 + 1.0,5 = 3,5 điểm
+ Thắng 4 trận thì số điểm là 4.1 = 4 điểm
Mà hạng 1 > hạng 2 nên số điểm của hạng 1 > số điểm của hạng 2.
Vậy hạng 1 đạt 3 điểm, hạng 2 đạt 2,5 điểm (3 > 2,5).
Do đó trận 1 – 4: hạng 4 thua, trận 2 – 4: hạng 4 hoà.
Ta có các kết quả như sau:
1 – 2: 2 thắng
1 – 3: 1 thắng
1 – 4: 1 thắng
1 – 5: 1 thắng
2 – 3: hoà
2 – 4: hoà
2 – 5: hoà
Ta thấy điểm của vận động viên 3, 4, 5 đang bằng nhau.
Còn lại 3 trận, tổng số điểm của ba trận là 3 điểm.
Vì các vận động viên không bằng điểm nhau nên ta kiểm tra các trường hợp:
+ Hạng 3 không thể thắng 2 trận vì như vậy sẽ bằng điểm hạng 2.
+ Hạng 3 không thể đạt 1 điểm, vì như vậy sẽ không thể cao hạng hơn hạng 4 và hạng 5.
Vậy hạng 3 đạt 1,5 điểm (hoà 1 trận, thắng 1 trận).
Vì hạng 4 không thắng trận nào nên hạng 4 đạt 1 điểm (hoà 2 trận, nếu không E sẽ nhiều điểm hơn D).
Vậy hạng 5 đạt 0,5 điểm (hoà 1 trận, thua 1 trận).
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5











