Đề thi giữa kì 1 Toán 9 - Đề số 5
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
-
A.
\(xy + x = 3\).
-
B.
\(x + y = xy\).
-
C.
\(2x - y = 0\).
-
D.
\({x^2} + {y^2} = 5\).
-
A.
\(2x + 0y = 5\).
-
B.
\(0x + 2y = 5\).
-
C.
\(0x - y = 2,5\).
-
D.
\( - 2x + 0y = 5\).
Đường thẳng đi qua hai điểm \(A\left( { - 2;0} \right)\) và \(B\left( { - 1;2} \right)\) là:
-
A.
\(y = 2x - 4\).
-
B.
\(y = - 2x - 4\).
-
C.
\(y = 2x + 4\).
-
D.
\(y = - 2x + 4\).
Nghiệm của phương trình \(\frac{{x + 1}}{{x - 2}} - 1 = \frac{{24}}{{\left( {x + 3} \right)\left( {x - 2} \right)}}\) là:
-
A.
\(x = 2\).
-
B.
\(x = - 3\).
-
C.
\(x = 5\).
-
D.
\(x = - 5\).
Nghiệm của phương trình \(\left( {x + 5} \right)\left( {2x - 10} \right) = 0\) là
-
A.
\(x = 5\).
-
B.
\(x \ne 5\).
-
C.
\(x = - 5\).
-
D.
\(x = - 5;x = 5\).
Nếu \(a < b\) và \(c < 0\) thì khẳng định nào sau đây là đúng?
-
A.
\(ac < bc\).
-
B.
\(a{c^2} > b{c^2}\).
-
C.
\(a{c^3} < b{c^3}\).
-
D.
\(ac > bc\).
Cho số thực x thỏa mãn \({x^2} < 9\). Khẳng định nào sau đây là đúng?
-
A.
\(x < 3\) hoặc \(x > - 3\).
-
B.
\(x < - 3\) hoặc \(x > 3\).
-
C.
\(x < 3\) và \(x > - 3\).
-
D.
\(x = - 3\) hoặc \(x > 3\).
Trong các giá trị sau của y, giá trị nhỏ nhất thỏa mãn bất phương trình \(2y + 10 \ge 25\)?
-
A.
5.
-
B.
7.
-
C.
8.
-
D.
10.
Với góc nhọn \(\alpha \), ta có:
-
A.
\({\rm{cos}}\left( {90^\circ - \alpha } \right) = \cot \alpha \).
-
B.
\(\sin \left( {90^\circ - \alpha } \right) = \tan \alpha \).
-
C.
\(\sin \left( {90^\circ - \alpha } \right) = \cot \alpha \).
-
D.
\(\sin \left( {90^\circ - \alpha } \right) = \cos \alpha \).
Cho tam giác ABC vuông tại A, có AB = 6cm và \(\cot C = \frac{3}{5}\). Độ dài AC bằng:
-
A.
\(\frac{9}{2}cm\).
-
B.
\(\frac{{15}}{2}cm\).
-
C.
\(\frac{{18}}{5}cm\).
-
D.
\(10cm\).
Cho tam giác ABC vuông tại A, có \(AB = \frac{2}{3}BC\). Tính \(\cot C\)
-
A.
\(\cot C = \frac{{3\sqrt 5 }}{5}\).
-
B.
\(\cot C = \frac{{\sqrt 5 }}{2}\).
-
C.
\(\cot C = \frac{6}{5}\).
-
D.
\(\cot C = \frac{{6\sqrt 5 }}{5}\).
Cho tam giác ABC vuông tại A có \(\widehat B = 30^\circ \) và \(AB = 10cm\). Độ dài cạnh BC bằng bao nhiêu?
-
A.
\(10\sqrt 3 cm\).
-
B.
\(20\sqrt 3 cm\).
-
C.
\(\frac{{10\sqrt 3 }}{3}cm\).
-
D.
\(\frac{{20\sqrt 3 }}{3}cm\).
Một nhóm gồm \(x\) bạn trẻ cùng tham gia khởi nghiệp và dự định góp vốn là 180 triệu đồng (số tiền mỗi người góp là như nhau). Nếu số người tham gia giảm đi 25% thì số tiền góp tăng lên 5 triệu đồng.
a) Nếu số người tham gia giảm đi 25% thì mỗi người góp \(\frac{{240}}{x}\) triệu đồng.
b) \(180x + 5 = 240x\).
c) \(x = 12\).
d) Nếu số người tham gia giảm đi 25% thì mỗi người góp 15 triệu.
Một trường học có 540 học sinh, biết mỗi lớp học có \(x\) học sinh và \(y\) chiếc ghế dài. Nếu xếp mỗi ghế 3 học sinh thì 6 học sinh không có chỗ. Nếu xếp mỗi ghế 4 học sinh thì thừa 1 ghế.
a) \(x - 3y = 6\).
b) \(x - 4y = 4\).
c) \(x = 36;y = 10\).
d) Trường học có 16 lớp học.
Chỉ số khối cơ thể - thường được biết đến với chữ viết tắt BMI theo tên tiếng Anh Body Mass Index - được dùng để đánh giá mức độ gầy hay béo của một người. Chỉ số này do nhà bác học người Bỉ Adolphe Quetelet đưa ra năm 1832.
Chỉ số khối cơ thể của một người được tính theo công thức sau: \(BMI = \frac{m}{{{h^2}}}\), trong đó m là khối lượng cơ thể tính theo kilôgam, h là chiều cao tính theo mét.
Dưới đây là bảng đánh giá thể trạng ở người lớn theo chỉ số BMI đối với khu vực châu Á – Thái Bình Dương:
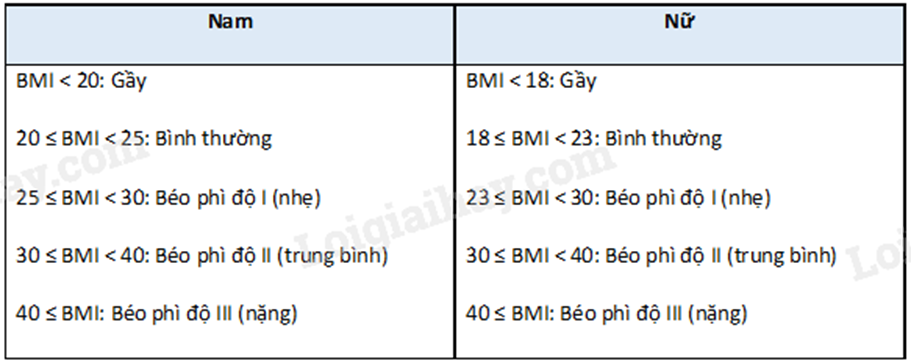
a) Bác Hùng có chiều cao 1,7m và cân nặng là 85kg, bác Hùng nên duy trì chế độ ăn và tập luyện hiện tại để có thể trạng bình thường.
b) Một người đàn ông cao 1,74m có thể trạng bình thường thì chỉ số cân nặng của người đó thỏa mãn \(60,552 \le m < 75,69\).
c) Một người phụ nữ cao 160cm có thể trạng gầy thì cân nặng của người đó thỏa mãn \(m \le 46,08\).
d) Bạn Mai cao 1,58m và nặng 40kg, bạn Mai cần tăng ít nhất khoảng 5 cân để có thể trạng bình thường.
Cho hình chữ nhật ABCD có AB = 5cm, BC = 12cm. Vẽ BH vuông góc với AC tại H. Tia BH cắt đường thẳng DC tại K và cắt AD tại N.
a) Độ dài AC là 13cm.
b) \(\sin ABH = \frac{5}{{12}}\).
c) \(AN.CK = AB.CH\).
d) \(\cot BAC + \cot BCA = \frac{{AB}}{{BH}}\)
Tính tích các nghiệm của phương trình \({\left( {{x^2} + x - 2} \right)^2} + 2{x^2} + 2x - 4 = 0\).
Đáp án:
Nghiệm \({x_0}\) của phương trình \(\frac{{{x^2}}}{{1 - 2x}} + \frac{{1 + 2x}}{4} = 1\) thỏa mãn biểu thức \(S = - 8x + 2025\).
Tính giá trị của S.
Đáp án:
Với m = 2, hệ phương trình \(\left\{ \begin{array}{l}2mx + 5y = 23\\3x + 3y = 15\end{array} \right.\) có cặp nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\) thỏa mãn biểu thức \(P = \frac{{{x_0}^2 + 4}}{{{y_0} + 5}} + 2024\). Tính giá trị của P.
Đáp án:
Trong buổi sáng đầu tiên của đợt hiến máu nhân đạo tổ chức ở một trường đại học, người ta đã thu được không dưới \(32900{\rm{ml}}\) máu. Theo thống kê thì sáng hôm đó có 40 người hiến máu ở mức \(350{\rm{ml}}\). Số còn lại hiến ở mức \(450{\rm{ml}}\). Hỏi trong buổi sáng hôm đó đã có ít nhất bao nhiêu người hiến máu ở mức \(450{\rm{ml}}\)?
Đáp án:
Một cây cau có chiều cao 6m. Để hái một buồng cau xuống, phải đặt thang tre sao cho đầu thang đạt độ cao đó. Khi đó góc của thang tre với mặt đất là bao nhiêu độ, biết chiếc thang dài 8m? (làm tròn đến độ)

Đáp án:
Hồ Giáo (1930 - 14 tháng 10 năm 2015), là đại biểu Quốc hội các khoá IV, V và VI. Ông là người duy nhất trong ngành chăn nuôi gia súc được nhà nước Việt Nam phong danh hiệu Anh hùng Lao động hai lần vào năm 1966 và 1986.
Trong câu truyện “Đàn bê của anh Hồ Giáo” (tiếng việt lớp 2). Giả sử, anh Hồ Giáo thả đàn bê trên một cánh đồng cỏ mọc dày như nhau, mọc cao đều như nhau trên toàn bộ cánh đồng trong suốt thời gian bê ăn cỏ trên cánh đồng ấy. Biết rằng, 9 con bê ăn hết cỏ trên cánh đồng trong 2 tuần, 6 con bê ăn hết cỏ trên cánh đồng trong 4 tuần. Hỏi bao nhiêu con bê ăn hết cỏ trên cánh đồng trong 6 tuần? ( xem như mỗi con bê ăn số cỏ như nhau)
Đáp án:
Lời giải và đáp án
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
-
A.
\(xy + x = 3\).
-
B.
\(x + y = xy\).
-
C.
\(2x - y = 0\).
-
D.
\({x^2} + {y^2} = 5\).
Đáp án : C
Phương trình bậc nhất hai ẩn là phương trình có dạng \(ax + by = c\) với a, b là hệ số cho trước và \(a \ne 0\) hoặc \(b \ne 0\).
Phương trình \(2x - y = 0\) là phương trình bậc nhất hai ẩn.
Đáp án C.
-
A.
\(2x + 0y = 5\).
-
B.
\(0x + 2y = 5\).
-
C.
\(0x - y = 2,5\).
-
D.
\( - 2x + 0y = 5\).
Đáp án : B
Tìm giao điểm của đường thẳng với trục Oy.
Thay tọa độ tìm được vào các phương trình.
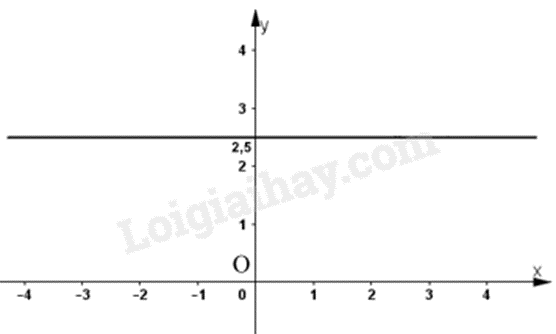
Quan sát hình vẽ, ta thấy đường thẳng biểu diễn tập nghiệm đi qua điểm \(\left( {0;2,5} \right)\).
Ta có \(0.0 + 2.2,5 = 5\) nên đây là hình minh họa tập nghiệm của phương trình \(0x + 2y = 5\).
Đáp án B.
Đường thẳng đi qua hai điểm \(A\left( { - 2;0} \right)\) và \(B\left( { - 1;2} \right)\) là:
-
A.
\(y = 2x - 4\).
-
B.
\(y = - 2x - 4\).
-
C.
\(y = 2x + 4\).
-
D.
\(y = - 2x + 4\).
Đáp án : C
Gọi đường thẳng cần tìm là \(y = ax + b\). Thay tọa độ điểm A và B vào phương trình đường thẳng.
Gọi đường thẳng cần tìm là \(y = ax + b\).
Vì đường thẳng đi qua hai điểm \(A\left( { - 2;0} \right)\) và \(B\left( { - 1;2} \right)\) nên ta có:
\(\left\{ \begin{array}{l}0 = - 2.a + b\\2 = - a + b\end{array} \right.\) suy ra \(\left( {a;b} \right) = \left( {2;4} \right)\).
Vậy phương trình đường thẳng cần tìm là \(y = 2x + 4\).
Đáp án C.
Nghiệm của phương trình \(\frac{{x + 1}}{{x - 2}} - 1 = \frac{{24}}{{\left( {x + 3} \right)\left( {x - 2} \right)}}\) là:
-
A.
\(x = 2\).
-
B.
\(x = - 3\).
-
C.
\(x = 5\).
-
D.
\(x = - 5\).
Đáp án : C
Tìm ĐKXĐ của phương trình.
Giải phương trình chứa ẩn ở mẫu.
ĐKXĐ: \(x - 2 \ne 0\) và \(x + 3 \ne 0\) hay \(x \ne 2\) và \(x \ne - 3\)
Ta có: \(\frac{{x + 1}}{{x - 2}} - 1 = \frac{{24}}{{\left( {x + 3} \right)\left( {x - 2} \right)}}\)
\(\begin{array}{l}\frac{{\left( {x + 1} \right)\left( {x + 3} \right)}}{{\left( {x + 3} \right)\left( {x - 2} \right)}} - \frac{{\left( {x + 3} \right)\left( {x - 2} \right)}}{{\left( {x + 3} \right)\left( {x - 2} \right)}} = \frac{{24}}{{\left( {x + 3} \right)\left( {x - 2} \right)}}\\\left( {x + 1} \right)\left( {x + 3} \right) - \left( {x + 3} \right)\left( {x - 2} \right) = 24\\{x^2} + 4x + 3 - {x^2} - x + 6 = 24\\{x^2} + 4x - {x^2} - x = 24 - 6 - 3\\3x = 15\\x = 5\left( {TM} \right)\end{array}\)
Đáp án C.
Nghiệm của phương trình \(\left( {x + 5} \right)\left( {2x - 10} \right) = 0\) là
-
A.
\(x = 5\).
-
B.
\(x \ne 5\).
-
C.
\(x = - 5\).
-
D.
\(x = - 5;x = 5\).
Đáp án : D
Giải phương trình tích để tìm nghiệm.
Ta có: \(\left( {x + 5} \right)\left( {2x - 10} \right) = 0\)
\(x + 5 \ne 0\) hoặc \(2x - 10 \ne 0\)
\(x \ne - 5\) hoặc \(x \ne 5\)
Vậy nghiệm của phương trình \(\left( {x + 5} \right)\left( {2x - 10} \right) = 0\) là \(x = - 5;x = 5\).
Đáp án D.
Nếu \(a < b\) và \(c < 0\) thì khẳng định nào sau đây là đúng?
-
A.
\(ac < bc\).
-
B.
\(a{c^2} > b{c^2}\).
-
C.
\(a{c^3} < b{c^3}\).
-
D.
\(ac > bc\).
Đáp án : D
Dựa vào tính chất của bất đẳng thức.
Ta có: \(a < b\) và \(c < 0\) thì \(ac > bc\) nên A sai, D đúng.
Vì \({c^2} \ge 0\) với mọi c nên \(a < b\) thì \(a{c^2} < b{c^2}\) nên B sai.
Với \(c < 0\) thì \({c^3} < 0\) nên \(a{c^3} > b{c^3}\) nên C sai.
Đáp án D.
Cho số thực x thỏa mãn \({x^2} < 9\). Khẳng định nào sau đây là đúng?
-
A.
\(x < 3\) hoặc \(x > - 3\).
-
B.
\(x < - 3\) hoặc \(x > 3\).
-
C.
\(x < 3\) và \(x > - 3\).
-
D.
\(x = - 3\) hoặc \(x > 3\).
Đáp án : C
Chuyển bất phương trình về \({x^2} - 9 < 0\)
Sử dụng hằng đẳng thức hiệu hai bình phương.
Vì tích của hai số là số âm nên hai số đó trái dấu.
Từ đó tìm \(x\) thỏa mãn.
Ta có: \({x^2} < 9\) nên \({x^2} - 9 < 0\) hay \(\left( {x - 3} \right)\left( {x + 3} \right) < 0\)
Ta biết rằng tích của hai số là số âm thì hai số đó trái dấu nên \(x - 3\) và \(x + 3\) trái dấu.
Mà \(x - 3 < x + 3\) nên \(x - 3 < 0\) và \(x + 3 > 0\)
Suy ra \(x < 3\) và \(x > - 3\)
Đáp án C.
Trong các giá trị sau của y, giá trị nhỏ nhất thỏa mãn bất phương trình \(2y + 10 \ge 25\)?
-
A.
5.
-
B.
7.
-
C.
8.
-
D.
10.
Đáp án : C
Giải bất phương trình bậc nhất một ẩn, từ đó suy ra giá trị nhỏ nhất thỏa mãn của y.
Ta có: \(2y + 10 \ge 25\)
\(\begin{array}{l}2y \ge 25 - 10\\2y \ge 15\\y \ge 7,5\end{array}\)
Do đó giá trị nhỏ nhất thỏa mãn bất phương trình là 8.
Đáp án C.
Với góc nhọn \(\alpha \), ta có:
-
A.
\({\rm{cos}}\left( {90^\circ - \alpha } \right) = \cot \alpha \).
-
B.
\(\sin \left( {90^\circ - \alpha } \right) = \tan \alpha \).
-
C.
\(\sin \left( {90^\circ - \alpha } \right) = \cot \alpha \).
-
D.
\(\sin \left( {90^\circ - \alpha } \right) = \cos \alpha \).
Đáp án : D
Dựa vào kiến thức về tỉ số lượng giác của hai góc phụ nhau.
Theo tỉ số lượng giác của hai góc phụ nhau, ta có \(\sin \left( {90^\circ - \alpha } \right) = \cos \alpha \).
Đáp án D.
Cho tam giác ABC vuông tại A, có AB = 6cm và \(\cot C = \frac{3}{5}\). Độ dài AC bằng:
-
A.
\(\frac{9}{2}cm\).
-
B.
\(\frac{{15}}{2}cm\).
-
C.
\(\frac{{18}}{5}cm\).
-
D.
\(10cm\).
Đáp án : C
Biểu diễn AC theo AB và \(\cot C\).
Xét tam giác ABC vuông tại A, ta có \(\cot C = \frac{{AC}}{{AB}}\) nên \(AC = AB.\cot C = 6.\frac{3}{5} = \frac{{18}}{5}\left( {cm} \right)\).
Đáp án C.
Cho tam giác ABC vuông tại A, có \(AB = \frac{2}{3}BC\). Tính \(\cot C\)
-
A.
\(\cot C = \frac{{3\sqrt 5 }}{5}\).
-
B.
\(\cot C = \frac{{\sqrt 5 }}{2}\).
-
C.
\(\cot C = \frac{6}{5}\).
-
D.
\(\cot C = \frac{{6\sqrt 5 }}{5}\).
Đáp án : B
Áp dụng định lí Pythagore tính AC theo AB và BC.
Biểu diễn \(\cot C\) trong tam giác ABC.
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {B{C^2} - {{\left( {\frac{2}{3}BC} \right)}^2}} = \sqrt {B{C^2} - \frac{4}{9}B{C^2}} = \frac{{\sqrt 5 }}{3}BC\)
Áp dụng tỉ số lượng giác của tam giác vuông vào tam giác ABC, ta có:
\(\cot C = \frac{{AC}}{{AB}} = \frac{{\frac{{\sqrt 5 }}{3}BC}}{{\frac{2}{3}BC}} = \frac{{\sqrt 5 }}{3}:\frac{2}{3} = \frac{{\sqrt 5 }}{2}\).
Đáp án B.
Cho tam giác ABC vuông tại A có \(\widehat B = 30^\circ \) và \(AB = 10cm\). Độ dài cạnh BC bằng bao nhiêu?
-
A.
\(10\sqrt 3 cm\).
-
B.
\(20\sqrt 3 cm\).
-
C.
\(\frac{{10\sqrt 3 }}{3}cm\).
-
D.
\(\frac{{20\sqrt 3 }}{3}cm\).
Đáp án : D
Biểu diễn BC theo AB và tỉ số lượng giác của góc B.
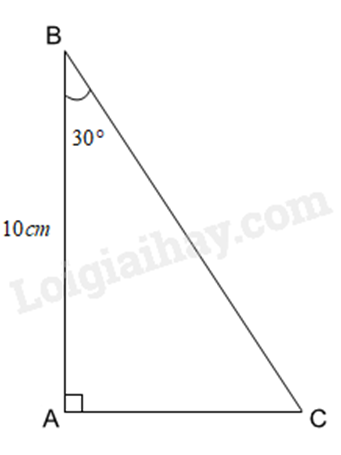
Áp dụng tỉ số lượng giác vào tam giác ABC, ta có:
\(\cos B = \frac{{AB}}{{BC}}\) suy ra \(BC = \frac{{AB}}{{\cos B}} = \frac{{10}}{{\cos 30^\circ }} = \frac{{20\sqrt 3 }}{3}\).
Đáp án D.
Một nhóm gồm \(x\) bạn trẻ cùng tham gia khởi nghiệp và dự định góp vốn là 180 triệu đồng (số tiền mỗi người góp là như nhau). Nếu số người tham gia giảm đi 25% thì số tiền góp tăng lên 5 triệu đồng.
a) Nếu số người tham gia giảm đi 25% thì mỗi người góp \(\frac{{240}}{x}\) triệu đồng.
b) \(180x + 5 = 240x\).
c) \(x = 12\).
d) Nếu số người tham gia giảm đi 25% thì mỗi người góp 15 triệu.
a) Nếu số người tham gia giảm đi 25% thì mỗi người góp \(\frac{{240}}{x}\) triệu đồng.
b) \(180x + 5 = 240x\).
c) \(x = 12\).
d) Nếu số người tham gia giảm đi 25% thì mỗi người góp 15 triệu.
a) Biểu diễn số tiền mỗi người góp và số tiền mỗi người góp nếu số người tham gia giảm đi 25% theo x.
b) Lập phương trình theo x.
c) Giải phương trình.
d) Tính số tiền mỗi người phải góp với giá trị x vừa tìm được.
ĐK: \(x \in {\mathbb{N}^*}\).
a) Nếu giảm đi 25% thì số người tham gia là:
\(x - 25\% x = 75\% x = \frac{3}{4}x\).
Khi đó, mỗi người góp số tiền là: \(\frac{{180}}{{\frac{3}{4}x}} = \frac{{240}}{x}\).
Vậy khẳng định a) đúng.
b) Với \(x\) người tham gia thì mỗi người góp số tiền là \(\frac{{180}}{x}\).
Vì nếu số người tham gia giảm đi 25% thì số tiền góp tăng lên 5 triệu đồng nên ta có phương trình:
\(\frac{{180}}{x} + 5 = \frac{{240}}{x}\).
Vậy khẳng định b) sai.
c) Giải phương trình:
\(\begin{array}{l}\frac{{180}}{x} + 5 = \frac{{240}}{x}\\\frac{{240}}{x} - \frac{{180}}{x} = 5\\\frac{{60}}{x} = 5\\x = 12\left( {TM} \right)\end{array}\)
Vậy khẳng định c) đúng.
d) Nếu số người tham gia giảm đi 25% thì mỗi người góp số tiền là: \(\frac{{240}}{{12}} = 20\) triệu.
Vậy khẳng định d) sai.
Đáp án a) Đ b) S c) Đ d) S.
Một trường học có 540 học sinh, biết mỗi lớp học có \(x\) học sinh và \(y\) chiếc ghế dài. Nếu xếp mỗi ghế 3 học sinh thì 6 học sinh không có chỗ. Nếu xếp mỗi ghế 4 học sinh thì thừa 1 ghế.
a) \(x - 3y = 6\).
b) \(x - 4y = 4\).
c) \(x = 36;y = 10\).
d) Trường học có 16 lớp học.
a) \(x - 3y = 6\).
b) \(x - 4y = 4\).
c) \(x = 36;y = 10\).
d) Trường học có 16 lớp học.
a) Viết phương trình dựa vào dữ kiện “Nếu xếp mỗi ghế 3 học sinh thì 6 học sinh không có chỗ”.
b) Viết phương trình dựa vào dữ kiện “Nếu xếp mỗi ghế 4 học sinh thì thừa 1 ghế”.
c) Từ hệ phương trình của hai phương trình của bài, giải để tìm x, y.
d) Tính số lớp học dựa vào số học sinh của trường và số học sinh mỗi lớp.
a) Vì nếu xếp mỗi ghế 3 học sinh thì 6 học sinh không có chỗ nên ta có phương trình:
\(3y + 6 = x\) hay \(x - 3y = 6\).
Vậy khẳng định a) đúng.
b) Vì nếu xếp mỗi ghế 4 học sinh thì thừa 1 ghế nên ta có phương trình:
\(4\left( {y - 1} \right) = x\) hay \(x - 4y = - 4\).
Vậy khẳng định b) sai.
c) Ta có hệ phương trình: \(\left\{ \begin{array}{l}x - 3y = 6\\x - 4y = - 4\end{array} \right.\).
Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}x = 36\\y = 10\end{array} \right.\).
Vậy khẳng định c) đúng.
d) Số lớp học của trường là: \(540:36 = 15\) (lớp).
Vậy khẳng định d) sai.
Đáp án a) Đ b) S c) Đ d) S.
Chỉ số khối cơ thể - thường được biết đến với chữ viết tắt BMI theo tên tiếng Anh Body Mass Index - được dùng để đánh giá mức độ gầy hay béo của một người. Chỉ số này do nhà bác học người Bỉ Adolphe Quetelet đưa ra năm 1832.
Chỉ số khối cơ thể của một người được tính theo công thức sau: \(BMI = \frac{m}{{{h^2}}}\), trong đó m là khối lượng cơ thể tính theo kilôgam, h là chiều cao tính theo mét.
Dưới đây là bảng đánh giá thể trạng ở người lớn theo chỉ số BMI đối với khu vực châu Á – Thái Bình Dương:

a) Bác Hùng có chiều cao 1,7m và cân nặng là 85kg, bác Hùng nên duy trì chế độ ăn và tập luyện hiện tại để có thể trạng bình thường.
b) Một người đàn ông cao 1,74m có thể trạng bình thường thì chỉ số cân nặng của người đó thỏa mãn \(60,552 \le m < 75,69\).
c) Một người phụ nữ cao 160cm có thể trạng gầy thì cân nặng của người đó thỏa mãn \(m \le 46,08\).
d) Bạn Mai cao 1,58m và nặng 40kg, bạn Mai cần tăng ít nhất khoảng 5 cân để có thể trạng bình thường.
a) Bác Hùng có chiều cao 1,7m và cân nặng là 85kg, bác Hùng nên duy trì chế độ ăn và tập luyện hiện tại để có thể trạng bình thường.
b) Một người đàn ông cao 1,74m có thể trạng bình thường thì chỉ số cân nặng của người đó thỏa mãn \(60,552 \le m < 75,69\).
c) Một người phụ nữ cao 160cm có thể trạng gầy thì cân nặng của người đó thỏa mãn \(m \le 46,08\).
d) Bạn Mai cao 1,58m và nặng 40kg, bạn Mai cần tăng ít nhất khoảng 5 cân để có thể trạng bình thường.
Dựa vào chiều cao và cân nặng để xác định chỉ số BMI của một người.
So sánh với số liệu trên bảng BMI.
a) Chỉ số BMI của bác Hùng là: \(BMI = \frac{{85}}{{1,{7^2}}} \approx 29,4\)
Ta có 25 ≤ 29,4 < 30 nên bác Hùng đang có thể trạng béo phì độ I (nhẹ).
Vì vậy nếu duy trì chế độ ăn và tập luyện hiện tại thì bác sẽ ở vẫn ở thể trạng béo phì độ I (nhẹ).
Vậy khẳng định a) sai.
b) Một người đàn ông có thể trạng bình thường thì 20 ≤ BMI < 25.
Với chiều cao 1,74m thì ta có:
\(\begin{array}{l}20 \le \frac{m}{{1,{{74}^2}}} < 25\\60,552 \le m < 75,69\end{array}\)
Vậy khẳng định b) đúng.
c) Ta có 160cm = 1,6m
Một người phụ nữ có thể trạng gầy thì BMI < 18.
\(\begin{array}{l}\frac{m}{{1,{6^2}}} < 18\\m < 18.1,{6^2}\\m < 46,08\end{array}\)
Vậy khẳng định c) sai.
d) Với chiều cao 1,58, để có thể trạng bình thường thì 18 ≤ BMI < 23
Suy ra \(18 \le \frac{m}{{1,{{58}^2}}} < 23\)
\(44,94 \le m < 57,42\)
Để có thể trạng bình thường thì ít nhất bạn Mai cần tăng số cân là: \(44,94 - 40 = 4,94 \approx 5\left( {kg} \right)\)
Vậy khẳng định d) đúng.
Đáp án a) S, b) Đ, c) S, d) Đ.
Cho hình chữ nhật ABCD có AB = 5cm, BC = 12cm. Vẽ BH vuông góc với AC tại H. Tia BH cắt đường thẳng DC tại K và cắt AD tại N.
a) Độ dài AC là 13cm.
b) \(\sin ABH = \frac{5}{{12}}\).
c) \(AN.CK = AB.CH\).
d) \(\cot BAC + \cot BCA = \frac{{AB}}{{BH}}\)
a) Độ dài AC là 13cm.
b) \(\sin ABH = \frac{5}{{12}}\).
c) \(AN.CK = AB.CH\).
d) \(\cot BAC + \cot BCA = \frac{{AB}}{{BH}}\)
a) Áp dụng định lí Pythagore vào tam giác ABC vuông tại B để tính AC.
b) Chứng minh suy ra \(\widehat {ABH} = \widehat {ACB}\) nên \(\sin ABH = \sin ACB\).
c) Sử dụng tỉ số lượng giác của góc ABN và góc CKH.
d) Biểu diễn \(\cot BAC\) và \(\cot BCA\) theo các cạnh.
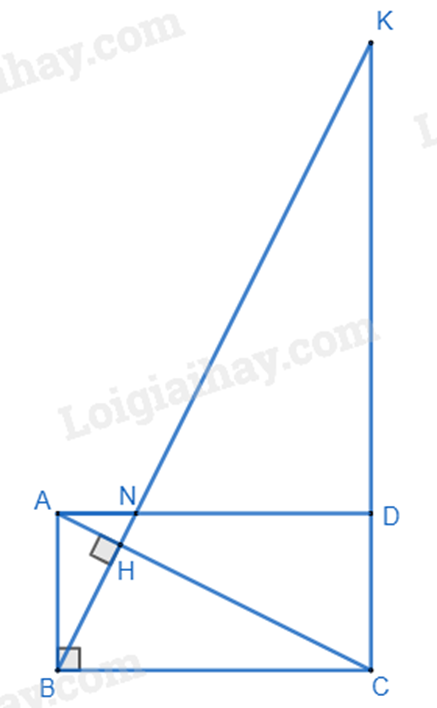
a) Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{5^2} + {{12}^2}} = 13\left( {cm} \right)\)
Vậy khẳng định a) đúng.
b) Xét tam giác AHB và tam giác ABC, ta có:
\(\widehat H = \widehat N\left( { = 90^\circ } \right)\)
\(\widehat A\) chung
Suy ra (g.g)
Do đó \(\widehat {ABH} = \widehat {ACB}\) (hai góc tương ứng)
Vì vậy \(\sin ABH = \sin ACB\).
Mà \(\sin ACB = \frac{{AB}}{{AC}} = \frac{5}{{13}}\) nên \(\sin ABH = \frac{5}{{13}}\).
Vậy khẳng định b) sai.
c) Áp dụng tỉ số lượng giác vào tam giác vuông ABN, ta có: \(\tan ABN = \frac{{AN}}{{AB}}\)
Áp dụng tỉ số lượng giác vào tam giác vuông CHK, ta có: \(\tan HKC = \frac{{CH}}{{HK}}\)
Mà \(\widehat {ABN} = \widehat {HKC}\) (hai góc so le trong) nên \(\tan ABN = \tan HKC\).
Do đó \(\frac{{AN}}{{AB}} = \frac{{CH}}{{HK}}\) nên \(AN.HK = AB.CH\)
Vì \(HK < CK\) (\(CK\) là cạnh huyền của tam giác vuông CHK) nên \(AN.CK > AN.HK = AB.CH\).
Vậy khẳng định c) sai.
d) \(\cot BAC + \cot BCA = \frac{{AB}}{{BH}}\)
Áp dụng tỉ số lượng giác, ta có:
\(\cot BAC + \cot BCA = \frac{{AH}}{{BH}} + \frac{{HC}}{{BH}} \\= \frac{{AH + HC}}{{BH}} = \frac{{AC}}{{BH}} > \frac{{AB}}{{BH}}.\)
Vậy khẳng định d) sai.
Đáp án a) Đ, b) S, c) S, d) S.
Tính tích các nghiệm của phương trình \({\left( {{x^2} + x - 2} \right)^2} + 2{x^2} + 2x - 4 = 0\).
Đáp án:
Đáp án:
Đưa phương trình về phương trình tích để giải.
Ta có: \({\left( {{x^2} + x - 2} \right)^2} + 2{x^2} + 2x - 4 = 0\)
\(\begin{array}{l}{\left( {{x^2} + x - 2} \right)^2} + 2\left( {{x^2} + x - 2} \right) = 0\\\left( {{x^2} + x - 2} \right)\left( {{x^2} + x - 2 + 2} \right) = 0\\\left( {{x^2} + x - 2} \right)\left( {{x^2} + x} \right) = 0\\\left( {{x^2} + x - 2} \right)x\left( {x + 1} \right) = 0\end{array}\)
Giải phương trình, ta thấy phương trình có một nghiệm \(x = 0\) nên tích các nghiệm của phương trình bằng 0.
Đáp án: 0
Vì tích của mọi số với 0 đều bằng 0.
Nghiệm \({x_0}\) của phương trình \(\frac{{{x^2}}}{{1 - 2x}} + \frac{{1 + 2x}}{4} = 1\) thỏa mãn biểu thức \(S = - 8x + 2025\).
Tính giá trị của S.
Đáp án:
Đáp án:
Giải bất phương tình để tìm \(x\). Thay giá trị x vừa tìm được vào S để tính giá trị của S.
ĐKXĐ: \(1 - 2x \ne 0\) hay \(x \ne \frac{1}{2}\).
Giải phương trình:
\(\begin{array}{l}\frac{{{x^2}}}{{1 - 2x}} + \frac{{1 + 2x}}{4} = 1\\\frac{{4{x^2}}}{{4\left( {1 - 2x} \right)}} + \frac{{\left( {1 + 2x} \right)\left( {1 - 2x} \right)}}{{4\left( {1 - 2x} \right)}} = \frac{{4\left( {1 - 2x} \right)}}{{4\left( {1 - 2x} \right)}}\\4{x^2} + \left( {1 + 2x} \right)\left( {1 - 2x} \right) = 4\left( {1 - 2x} \right)\\4{x^2} + 1 - 4{x^2} = 4 - 8x\\8x = 3\\x = \frac{3}{8}\left( {TM} \right)\end{array}\)
Thay vào S, ta được: \(S = - 8.\frac{3}{8} + 2025 = - 3 + 2025 = 2022\).
Đáp án: 2022
Với m = 2, hệ phương trình \(\left\{ \begin{array}{l}2mx + 5y = 23\\3x + 3y = 15\end{array} \right.\) có cặp nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\) thỏa mãn biểu thức \(P = \frac{{{x_0}^2 + 4}}{{{y_0} + 5}} + 2024\). Tính giá trị của P.
Đáp án:
Đáp án:
Thay m = 2 vào hệ phương trình để tìm cặp nghiệm.
Thay cặp nghiệm vào P để tính giá trị của P.
Tại m = 2, ta có: \(\left\{ \begin{array}{l}2.2x + 5y = 23\\3x + 3y = 15\end{array} \right.\) hay \(\left\{ \begin{array}{l}4x + 5y = 23\\3x + 3y = 15\end{array} \right.\).
Giải phương trình ta được cặp nghiệm \(\left( {{x_0};{y_0}} \right) = \left( {2;3} \right)\).
Thay vào P, ta được:
\(P = \frac{{{2^2} + 4}}{{3 + 5}} + 2024 = 1 + 2024 = 2025\).
Đáp án: 2025
Trong buổi sáng đầu tiên của đợt hiến máu nhân đạo tổ chức ở một trường đại học, người ta đã thu được không dưới \(32900{\rm{ml}}\) máu. Theo thống kê thì sáng hôm đó có 40 người hiến máu ở mức \(350{\rm{ml}}\). Số còn lại hiến ở mức \(450{\rm{ml}}\). Hỏi trong buổi sáng hôm đó đã có ít nhất bao nhiêu người hiến máu ở mức \(450{\rm{ml}}\)?
Đáp án:
Đáp án:
Gọi số người hiến máu ở mức 450ml là x (người), \(x \in {\mathbb{N}^*}\).
Biểu diễn bất phương trình theo x.
Gọi số người hiến máu ở mức 450ml là x (người), \(x \in {\mathbb{N}^*}\).
Vì tổng số máu thu được không dưới 32900ml và có 40 người hiến máu ở mức \(350{\rm{ml}}\) nên ta có bất phương trình: \(450x + 40.350 \ge 32900\)
Giải bất phương trình:
\(\begin{array}{l}450x + 40.350 \ge 32900\\450x + 14000 \ge 32900\\450x \ge 18900\\x \ge 42\end{array}\)
Vậy có ít nhất 42 người hiến máu ở mức 450ml.
Đáp án: 42
Một cây cau có chiều cao 6m. Để hái một buồng cau xuống, phải đặt thang tre sao cho đầu thang đạt độ cao đó. Khi đó góc của thang tre với mặt đất là bao nhiêu độ, biết chiếc thang dài 8m? (làm tròn đến độ)

Đáp án:
Đáp án:
Sử dụng kiến thức về tỉ số lượng giác để tính góc của thang tre với mặt đất.
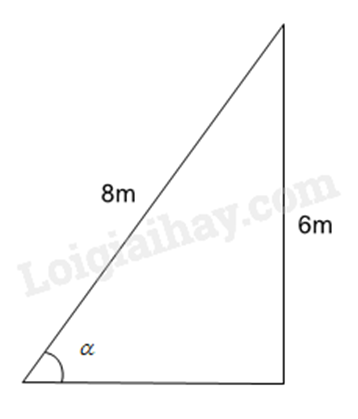
Áp dụng tỉ số lượng giác ta có: \(\sin \alpha = \frac{6}{8} = \frac{3}{4}\) suy ra \(\alpha \approx 49^\circ \)
Vậy góc tạo bởi thang tre với mặt đất khoảng \(49^\circ \).
Hồ Giáo (1930 - 14 tháng 10 năm 2015), là đại biểu Quốc hội các khoá IV, V và VI. Ông là người duy nhất trong ngành chăn nuôi gia súc được nhà nước Việt Nam phong danh hiệu Anh hùng Lao động hai lần vào năm 1966 và 1986.
Trong câu truyện “Đàn bê của anh Hồ Giáo” (tiếng việt lớp 2). Giả sử, anh Hồ Giáo thả đàn bê trên một cánh đồng cỏ mọc dày như nhau, mọc cao đều như nhau trên toàn bộ cánh đồng trong suốt thời gian bê ăn cỏ trên cánh đồng ấy. Biết rằng, 9 con bê ăn hết cỏ trên cánh đồng trong 2 tuần, 6 con bê ăn hết cỏ trên cánh đồng trong 4 tuần. Hỏi bao nhiêu con bê ăn hết cỏ trên cánh đồng trong 6 tuần? ( xem như mỗi con bê ăn số cỏ như nhau)
Đáp án:
Đáp án:
Đây là một bài toán khó, đòi hỏi học sinh phải đọc thật kỹ đề và tư duy. Bài toán khó ở 2 chỗ :
+ Trong suốt thời gian bò ăn cỏ, cỏ vẫn mọc đều trên cánh đồng.
+ Học sinh phải biết chọn 1 làm đơn vị khối lượng cỏ ban đầu, nếu học sinh không biết kỹ thuật này sẽ gọi thêm một ẩn nữa và bài toán sẽ có 3 ẩn số, rất khó để giải. ( kỹ thuật giải này thường sử dụng trong môn Hóa Học, và gần đây được sử dụng trong môn Vật Lý với tên gọi ”chuẩn hóa”)
Học sinh có thể sẽ yếu kiến thức về bài toán tỉ lệ nghịch, tỉ lệ thuận làm cho việc lập ra biểu thức diễn tả mối quan hệ giữa các đại lượng gặp khó khăn. Ở bài toán này các em có thể sẽ khó hiểu ở đoạn:
9 con bê ăn trong 2 tuần hết 1 + 2y nên mỗi con bê ăn trong một tuần hết ăn hết \(\frac{{1 + 2y}}{{18}}\)
Đặt câu hỏi: Tại sao mỗi con bê lại ăn hết \(\frac{{1 + 2y}}{{18}}\) . Số \(\frac{{1 + 2y}}{{18}}\) ở đâu mà ra?
Giải thích đơn giản thế này:
9 con bê ăn trong 2 tuần hết \(1 + 2y{\rm{\;\;}}\)suy ra 9 con bê ăn trong 1 tuần hết \(\frac{{1 + 2y}}{2}\) ( tức là chỉ ăn hết 1 nửa thôi)
9 con bê ăn trong 1 tuần hết \(\frac{{1 + 2y}}{2}\) suy ra mỗi con bê ăn trong một tuần hết ăn hết \(\frac{{1 + 2y}}{2}:9 = \frac{{1 + 2y}}{{18}}\).
Gọi khối lượng cỏ có sẵn trên cánh đồng trước khi bò ăn cỏ là 1. ( đơn vị khối lượng quy ước)
Khối lượng cỏ mọc thêm trên cánh đồng trong một tuần là \(y\) (với cùng đơn vị khối lượng ở trên), \(y > 0\).
Gọi số bê phải tìm là \(x\) con, (\(x \in {\mathbb{N}^*}\))
* Theo đề bài:
9 con bê ăn trong 2 tuần hết \(1 + 2y\) nên mỗi con bê ăn trong một tuần hết ăn hết \(\frac{{1 + 2y}}{{18}}\)
6 con bê ăn trong 4 tuần hết \(1 + 4y\) nên mỗi con bê ăn trong một tuần hết ăn hết \(\frac{{1 + 4y}}{{24}}{\rm{\;}}\)
x con bê ăn trong 6 tuần hết \(1 + 6y\) nên mỗi con bê ăn trong một tuần hết ăn hết \(\frac{{1 + 6y}}{{6x}}\)
Ta có hệ phương trình:
\(\left\{ \begin{array}{l}\frac{{1 + 2y}}{{18}} = \frac{{1 + 4y}}{{24}}\\\frac{{1 + 4y}}{{24}} = \frac{{1 + 6y}}{{6x}}\end{array} \right.\) hay \(\left\{ \begin{array}{l}4\left( {1 + 2y} \right) = 3\left( {1 + 4y} \right)\\x\left( {1 + 4y} \right) = 4\left( {1 + 6y} \right)\end{array} \right.\)
Suy ra \(\left\{ \begin{array}{l}4 + 8y = 3 + 12y\\x\left( {1 + 4y} \right) = 4\left( {1 + 6y} \right)\end{array} \right.\). Rút gọn phương trình thứ nhất ta được \(\left\{ \begin{array}{l}4y = 1\\x\left( {1 + 4y} \right) = 4\left( {1 + 6y} \right)\end{array} \right.\).
Từ đó suy ra \(\left\{ \begin{array}{l}y = \frac{1}{4}\\x.2 = 10\end{array} \right.\).
Ta tính được \(\left\{ \begin{array}{l}y = \frac{1}{4}\left( {TM} \right)\\x = 5\left( {TM} \right)\end{array} \right.\).
Vậy 5 con bê của anh Hồ Giáo ăn trong 6 tuần thì hết cánh đồng cỏ.
Đáp án: 5
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau: Câu 1: Nghiệm của phương trình \(x + 2y = 5\) là
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau: Câu 1: Nghiệm của phương trình \(x + 2y = 0\) là:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau: Câu 1: Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn?
Các bài khác cùng chuyên mục
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5










Danh sách bình luận