Giải đề thi học kì 2 toán lớp 10 năm 2020 - 2021 trường Đốc Binh Kiều
Làm đề thiCâu hỏi 1 :
Câu 1:
Xét dấu biểu thức \(f\left( x \right) = - {x^2} + 4x + 5\)
Phương pháp giải:
Giải phương trình f(x)=0.
\(a{x^2} + bx + c = 0\) có 2 nghiệm phân biệt \({x_1} < {x_2}\) thì tam thức cùng dấu với a khi \(x \in \left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\) và trái dấu với a khi \(x \in \left( {{x_1},{x_2}} \right)\)
Lời giải chi tiết:
\( - {x^2} + 4x + 5 = 0\) có 2 nghiệm phân biệt \(x = - 1;x = 5\).
Khi đó \(f\left( x \right) = - {x^2} + 4x + 5 > 0\) ( trái dấu với -1) khi \(x \in \left( { - 1;5} \right)\) và \(f\left( x \right) = - {x^2} + 4x + 5 < 0\) (cùng dấu với -1) khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {5; + \infty } \right)\)
Câu 2:
Giải bất phương trình \(\left( {x - 1} \right)\left( {{x^2} - 5x + 6} \right) \ge 0\)
Phương pháp giải:
Lập bảng xét dấu.
Lời giải chi tiết:
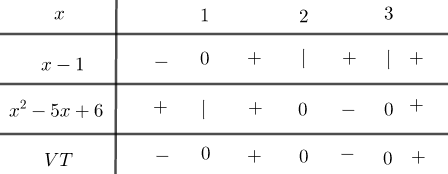
Câu 3:
Giải bất phương trình \(\dfrac{{x + 2}}{{1 - {x^2}}} > 2\)
Phương pháp giải:
Chuyển 2 sang vế trái rồi quy đồng.
Lập bảng xét dấu.
Lời giải chi tiết:
\(\begin{array}{l}\dfrac{{x + 2}}{{1 - {x^2}}} > 2 \Leftrightarrow \dfrac{{x + 2}}{{1 - {x^2}}} - 2 > 0\\ \Leftrightarrow \dfrac{{2{x^2} + x}}{{1 - {x^2}}} > 0 \Leftrightarrow \dfrac{{x\left( {2x + 1} \right)}}{{\left( {1 - x} \right)\left( {1 + x} \right)}} > 0\end{array}\)
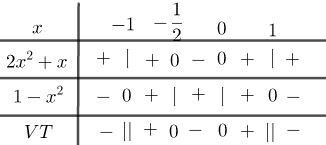
Câu hỏi 2 :
Câu 1:
Cho \(\sin x = \dfrac{4}{5}\left( {0 < x < \dfrac{\pi }{2}} \right)\). Tính \(\cos x,\tan x,\cot x\).
Phương pháp giải:
Sử dụng công thức: \({\sin ^2}x + {\cos ^2}x = 1;\)
\(0 < x < \dfrac{\pi }{2} \Rightarrow \cos x > 0\)
Lời giải chi tiết:
\(\begin{array}{l}{\sin ^2}x + {\cos ^2}x = 1 \Rightarrow {\cos ^2}x = \dfrac{9}{{25}}\\ \Rightarrow \left| {\cos x} \right| = \dfrac{3}{5}\end{array}\)
\(\begin{array}{l}0 < x < \dfrac{\pi }{2} \Rightarrow \cos x = \dfrac{3}{5}\\ \Rightarrow \tan x = \dfrac{{\sin x}}{{\cos x}} = \dfrac{4}{3}\\ \Rightarrow \cot x = \dfrac{1}{{\tan x}} = \dfrac{3}{4}\end{array}\)
Câu 2:
Chứng minh rằng: \(\dfrac{{1 + \sin 2\alpha - \cos 2\alpha }}{{1 + \cos 2\alpha }} = \tan \alpha + {\tan ^2}\alpha \)
Phương pháp giải:
Sử dụng công thức: \(\sin 2\alpha = 2\sin \alpha .\cos \alpha \)
\(2{\cos ^2}\alpha = 1 + \cos 2\alpha \)\(;2{\sin ^2}\alpha = 1 - \cos 2\alpha \)
Lời giải chi tiết:
\(\begin{array}{l}VT = \dfrac{{1 + \sin 2\alpha - \cos 2\alpha }}{{1 + \cos 2\alpha }}\\ = \dfrac{{2{{\sin }^2}\alpha + 2\sin \alpha .\cos \alpha }}{{2{{\cos }^2}\alpha }}\\ = {\left( {\dfrac{{\sin \alpha }}{{\cos \alpha }}} \right)^2} + \dfrac{{\sin \alpha }}{{\cos \alpha }}\\ = {\tan ^2}\alpha + \tan \alpha = VP\end{array}\)
Câu hỏi 3 :
Câu 1:
Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình tổng quát của đường thẳng đi qua hai điểm A, B biết A(2;1), B(4;3).
Phương pháp giải:
Tìm \(\overrightarrow {AB} \).
Lời giải chi tiết:
\(\overrightarrow {AB} = \left( {2;2} \right)\)=> AB nhận vecto \(\overrightarrow n = \left( {1; - 1} \right)\) làm vtpt nên có phương trình:
\(\begin{array}{l}AB:1\left( {x - 2} \right) - \left( {y - 1} \right) = 0\\ \Leftrightarrow x - y - 1 = 0\end{array}\)
Câu 2:
Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình đường tròn có tâm \(I\left( {2; - 3} \right)\) và đi qua \(M\left( {1;4} \right)\).
Phương pháp giải:
(C) tâm I qua M nên có R=IM.
Phương trình (C) qua \(I\left( {{x_0};{y_0}} \right)\) và có bán kính R: \({\left( {x - {x_0}} \right)^2} + {\left( {y - {y_0}} \right)^2} = {R^2}\)
Lời giải chi tiết:
(C) tâm I qua M nên có \({R^2} = I{M^2} = 50\).
Phương trình (C) qua \(I\left( {2; - 3} \right)\) và đi qua \(M\left( {1;4} \right)\): \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 50\)
Câu 3:
Trong mặt phẳng với hệ tọa độ Oxy, tìm tọa độ điểm M thuộc đường thẳng \(d:2x - y + 3 = 0\) và cách điểm \(A\left( {3; - 2} \right)\) một khoảng bằng 5.
Phương pháp giải:
Tham số hóa điểm M: \(M \in \left( d \right) \Rightarrow M\left( {m;2m + 3} \right)\)
Lời giải chi tiết:
\(M \in \left( d \right) \Rightarrow M\left( {m;2m + 3} \right)\)
\(\begin{array}{l}AM = 5 \Rightarrow A{M^2} = 25\\ \Leftrightarrow {\left( {m - 3} \right)^2} + {\left( {2m + 5} \right)^2} = 25\\ \Leftrightarrow 5{m^2} + 14m + 9 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = - \dfrac{9}{5}\end{array} \right.\end{array}\)
Câu hỏi 4 :
Câu 1:
Tìm các giá trị của tham số m để phương trình sau có 2 nghiệm trái dấu:
\( - 2{x^2} + {m^2}x + {m^2} - 4 = 0\)
Phương pháp giải:
\(a{x^2} + bx + c = 0\) có 2 nghiệm trái dấu \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\P = \dfrac{c}{a} < 0\end{array} \right.\)
Lời giải chi tiết:
\( - 2{x^2} + {m^2}x + {m^2} - 4 = 0\) có 2 nghiệm trái dấu
\(\begin{array}{l} \Leftrightarrow P = \dfrac{{{m^2} - 4}}{{ - 2}} < 0\\ \Leftrightarrow {m^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < - 2\end{array} \right.\end{array}\)
Câu 2:
Tìm m để bất phương trình sau nghiệm đúng với mọi \(x \in \mathbb{R}\):
\(\left( {{m^2} + 2} \right){x^2} - 2\left( {m - 2} \right)x + 2 \ge 0\)
Phương pháp giải:
\(a{x^2} + bx + c \ge 0\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta ' \le 0\end{array} \right.\)
Lời giải chi tiết:
\(\left( {{m^2} + 2} \right){x^2} - 2\left( {m - 2} \right)x + 2 \ge 0\)\( \Leftrightarrow \Delta ' \le 0\) vì \(\left( {{m^2} + 2} \right) > 0\forall m\)
\(\begin{array}{l} \Leftrightarrow {\left( {m - 2} \right)^2} - 2\left( {{m^2} + 2} \right) \le 0\\ \Leftrightarrow - {m^2} - 4m \le 0\\ \Leftrightarrow \left[ \begin{array}{l}m \ge 0\\m \le - 4\end{array} \right.\end{array}\)
Luyện Bài tập trắc nghiệm môn Toán lớp 10 - Xem ngay
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2020 - 2021 trường THPT Nguyễn Xuân Ôn với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2019 - 2020 trường THCS & THPT Nguyễn Tất Thành với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2019 - 2020 trường THPT Yên Mỹ - Hưng Yên với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2019 - 2020 trường THPT Yên Hòa - Hà Nội với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2019 - 2020 trường THPT Phú Lương - Thái Nguyên với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2019 - 2020 trường THPT Đống Đa - Hà Nội với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2019 - 2020 Sở GD&ĐT Bắc Ninh với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2020 - 2021 trường THPT Lấp Vò 1 với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2020 - 2021 trường THPT Phan Đình Phùng với cách giải nhanh và chú ý quan trọng
Giải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2020 - 2021 trường THPT Trần Quang Khải với cách giải nhanh và chú ý quan trọng
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |









