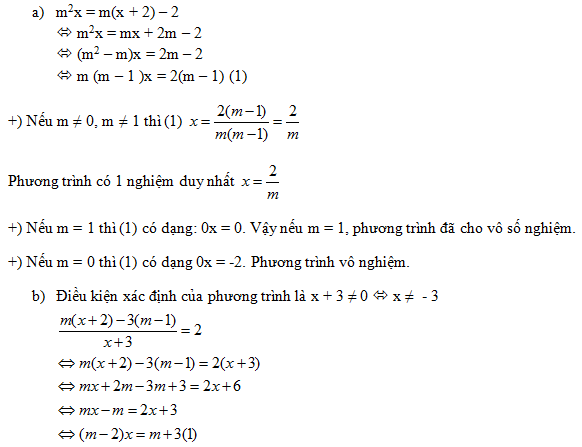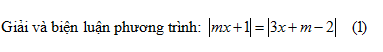60 bài tập trắc nghiệm phương trình mức độ vận dụng
Làm đề thiCâu hỏi 1 :
Phương trình \({\left( {x + 1} \right)^2} = 3x + 9\) là phương trình hệ quả của phương trình nào sau đây?
- A \(\sqrt {x + 1} = 3x + 9\)
- B \(\sqrt {x + 1} = \sqrt {3x - 9} \)
- C \(x + 1 = \sqrt {3x + 9} \)
- D \(x + 1 = 3\left( {x + 3} \right)\)
Đáp án: C
Phương pháp giải:
\(\begin{array}{l} + )\,\,{\left( {x + 1} \right)^2} = 3x + 9 \Leftrightarrow {x^2} - x - 8 = 0 \Leftrightarrow x = \frac{{1 \pm \sqrt {33} }}{2}\\ + )\,\,\sqrt {x + 1} = 3x - 9 \Leftrightarrow \left\{ \begin{array}{l}3x + 9 \ge 0\\x + 1 = 9{x^2} - 54x + 81\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\x = \frac{{55 \pm \sqrt {145} }}{{18}}\end{array} \right.\\ + )\,\,\sqrt {x + 1} = \sqrt {3x - 9} \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\3x - 9 \ge 0\\x + 1 = 3x - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\x \ge 3\\2x = 10\end{array} \right. \Leftrightarrow x = 5\\ + )\,\,x + 1 = \sqrt {3x + 9} \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\{x^2} + 2x + 1 = 3x + 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\{x^2} - x - 8 = 0\end{array} \right. \Leftrightarrow x = \frac{{1 + \sqrt {33} }}{2}\\ + )\,\,x + 1 = 3\left( {x + 3} \right) \Leftrightarrow x + 1 = 3x + 9 \Leftrightarrow 2x = - 8 \Leftrightarrow x = - 4\end{array}\)
Vậy phương trình \({\left( {x + 1} \right)^2} = 3x + 9\) là phương trình hệ quả của phương trình \(x + 1 = \sqrt {3x + 9} \).
Chọn đáp án C.
Lời giải chi tiết:
Nếu mọi nghiệm của phương trình \(f\left( x \right) = 0\) đều là nghiệm của phương trình \(g\left( x \right) = 0\) thì \(g\left( x \right) = 0\) được gọi là phương trình hệ quả của phương trình \(f\left( x \right) = 0\).
Câu hỏi 2 :
Giải phương trình \({x^2} + \frac{1}{{\sqrt {1 - x} }} = 3x + \frac{1}{{\sqrt {1 - x} }}\,\,\,\left( 1 \right)\)
- A \(x = 1\)
- B \(x = 2\)
- C \(x = 3\)
- D \(x = 4\)
Đáp án: A
Phương pháp giải:
+) Tìm TXĐ.
+) Rút gọn và giải phương trình.
Lời giải chi tiết:
ĐK: \(1 - x > 0 \Leftrightarrow x < 1\)
\({x^2} + \frac{1}{{\sqrt {1 - x} }} = 3x + \frac{1}{{\sqrt {1 - x} }} \Leftrightarrow {x^2} - 3x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\left( {tm} \right)\\x = 3\,\,\left( {ktm} \right)\end{array} \right.\)
Vậy \(x = 1\) là nghiệm của phương trình.
Câu hỏi 3 :
Khẳng định nào sau đây là sai?
- A \(\sqrt {x - 2} = 1 \Rightarrow x - 2 = 1\)
- B \(\dfrac{{x\left( {x - 1} \right)}}{{x - 1}} = 1 \Rightarrow x = 1\)
- C \(\left| {3x - 2} \right| = x - 3 \Rightarrow 8{x^2} - 4x - 5 = 0\)
- D \(\sqrt {x - 3} = \sqrt {9 - 2x} \Rightarrow 3x - 12 = 0\)
Đáp án: C
Phương pháp giải:
Dựa vào khái niệm phương trình hệ quả: Nếu mỗi nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) đều là nghiệm của phương trình \(h\left( x \right) = k\left( x \right)\) thì phương trình \(h\left( x \right) = k\left( x \right)\) được gọi là phương trình hệ quả của phương trình \(f\left( x \right) = g\left( x \right)\) (nghĩa là tập hợp nghiệm của phương trình \(h\left( x \right) = k\left( x \right)\) chứa tập nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\)).
Lời giải chi tiết:
Xét đáp án C ta có:
\(\begin{array}{l} + )\,\,\left| {3x - 2} \right| = x - 3 \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\{\left( {3x - 2} \right)^2} = {\left( {x - 3} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\{\left( {3x - 2} \right)^2} - {\left( {x - 3} \right)^2} = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left( {4x - 5} \right)\left( {2x + 1} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = \dfrac{5}{4}\\x = - \dfrac{1}{2}\end{array} \right.\,\,\left( {ktm} \right)\end{array} \right. \Leftrightarrow x \in \emptyset \Rightarrow {S_1} = \emptyset \\ + )\,\,8{x^2} - 4x - 5 = 0 \Leftrightarrow x = \dfrac{{1 \pm \sqrt {11} }}{4} \Rightarrow {S_2} = \left\{ {\dfrac{{1 \pm \sqrt {11} }}{4}} \right\}\end{array}\)
Do nên đáp án C sai.
Chọn C.
Câu hỏi 4 :
Cho hai phương trình \(x\left( {x - 2} \right) = 3\left( {x - 2} \right)\) (1) và \(\dfrac{{x\left( {x - 2} \right)}}{{x - 2}} = 3\,\,\left( 2 \right)\). Khẳng định nào sau đây là đúng?
- A Phương trình (1) là hệ quả của phương trình (2).
- B Phương trình (1) và (2) là hai phương trình tương đương.
- C Phương trình (2) là hệ quả của phương trình (1).
- D Cả A, B, C đều sai.
Đáp án: A
Phương pháp giải:
Xác định tập nghiệm của mỗi phương trình (1) và (2) sau đó dựa vào khái niệm phương trình hệ quả để kết luận.
Lời giải chi tiết:
Xét phương trình (1) ta có \(x\left( {x - 2} \right) = 3\left( {x - 2} \right) \Leftrightarrow \left( {x - 2} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 3\end{array} \right. \Rightarrow {S_1} = \left\{ {2;3} \right\}\).
Xét phương trình (2) ta có:
ĐK: \(x - 2 \ne 0 \Leftrightarrow x \ne 2\).
\(\dfrac{{x\left( {x - 2} \right)}}{{x - 2}} = 3 \Leftrightarrow \dfrac{{x\left( {x - 2} \right) - 3\left( {x - 2} \right)}}{{x - 2}} = 0 \Leftrightarrow \left( {x - 2} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {ktm} \right)\\x = 3\,\,\left( {tm} \right)\end{array} \right. \Rightarrow {S_2} = \left\{ 3 \right\}\).
Vì \({S_2} \subset {S_1}\) nên phương trình phương trình (1) là phương trình hệ quả của phương trình (2).
Chọn A.
Câu hỏi 5 :
Phương trình \(\left( {{x^2} - x - 2} \right)\sqrt {x + 1} = 0\) có bao nhiêu nghiệm?
- A 0
- B 1
- C 2
- D 3
Đáp án: C
Phương pháp giải:
Giải phương trình dạng \(f\left( x \right)g\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\g\left( x \right) = 0\end{array} \right.\). Lưu ý ĐKXĐ của phương trình.
Lời giải chi tiết:
ĐKXĐ: \(x + 1 \ge 0 \Leftrightarrow x \ge - 1\).
\(\left( {{x^2} - x - 2} \right)\sqrt {x + 1} = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - x - 2 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left( {x + 1} \right)\left( {x - 2} \right) = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\,\,\left( {tm} \right)\).
Vậy phương trình đã cho có 2 nghiệm.
Chọn C.
Câu hỏi 6 :
Khẳng định nào sau đây là sai?
- A \(\sqrt {x - 1} = 2\sqrt {1 - x} \Leftrightarrow x - 1 = 0\)
- B \({x^2} + 1 = 0 \Leftrightarrow \dfrac{{x - 1}}{{\sqrt {x - 1} }} = 0\)
- C \(\left| {x - 2} \right| = \left| {x + 1} \right| \Leftrightarrow {\left( {x - 2} \right)^2} = {\left( {x + 1} \right)^2}\)
- D \({x^2} = 1 \Leftrightarrow x = 1\)
Đáp án: D
Phương pháp giải:
Hai phương trình được gọi là tương đương khi chúng có cùng tập hợp nghiệm.
Lời giải chi tiết:
Xét đáp án D ta có \({x^2} = 1 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x + 1} \right) = 0 \Leftrightarrow x = \pm 1\).
Do đó đáp án D sai.
Chọn D.
Câu hỏi 7 :
Điều kiện xác định của phương trình \(\dfrac{{\sqrt {2x + 1} }}{{{x^2} + 3x}} = 0\) là:
- A \(x \ge \dfrac{{ - 1}}{2}\)
- B \(x \ge \dfrac{{ - 1}}{2}\) và \(x \ne - 3\)
- C \(x \ge \dfrac{{ - 1}}{2}\) và \(x \ne 0\)
- D \(x \ne - 3\) và \(x \ne 0\)
Đáp án: C
Phương pháp giải:
+) \(\sqrt A \) xác định (có nghĩa) \( \Leftrightarrow A \ge 0\).
+) Phân thức xác định khi và chỉ khi mẫu thức khác 0.
Lời giải chi tiết:
Phương trình xác định \( \Leftrightarrow \left\{ \begin{array}{l}2x + 1 \ge 0\\{x^2} + 3x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{{ - 1}}{2}\\x \ne 0\\x \ne - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{{ - 1}}{2}\\x \ne 0\end{array} \right.\).
Chọn C.
Câu hỏi 8 :
Điều kiện xác định của phương trình \(x + 2 - \dfrac{1}{{\sqrt {x + 2} }} = \dfrac{{\sqrt {4 - 3x} }}{{x + 1}}\) là:
- A \(x > - 2\) và \(x \ne - 1\)
- B \(x > - 2\) và \(x < \dfrac{4}{3}\)
- C \(x > 2,\,\,x \ne - 1,\,\,x \le \dfrac{4}{3}\)
- D \(x \ne - 2\) và \(x \ne - 1\)
Đáp án: C
Phương pháp giải:
+) \(\sqrt A \) xác định (có nghĩa) \( \Leftrightarrow A \ge 0\).
+) Phân thức xác định khi và chỉ khi mẫu thức khác 0.
Lời giải chi tiết:
ĐKXĐ: \(\left\{ \begin{array}{l}4 - 3x \ge 0\\x + 2 \ge 0\\\sqrt {x + 2} \ne 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le \dfrac{4}{3}\\x \ge - 2\\x \ne - 2\\x \ne - 1\end{array} \right. \Leftrightarrow - 2 < x \le \dfrac{4}{3},\,\,x \ne - 1\).
Chọn C.
Câu hỏi 14 :
Số nghiệm của phương trình \(\left( {\sqrt 5 - 1} \right){x^4} + 5{x^2} + 7\left( {1 - \sqrt 2 } \right) = 0\) là:
- A 0
- B 1
- C 2
- D 4
Đáp án: C
Phương pháp giải:
Giải phương trình trùng phương bằng cách đặt \({x^2} = t\,\,\left( {t \ge 0} \right)\)
Lời giải chi tiết:
Đặt \({x^2} = t\,\,\left( {t \ge 0} \right)\) khi đó phương trình trở thành \(\left( {\sqrt 5 - 1} \right){t^2} + 5t + 7\left( {1 - \sqrt 2 } \right) = 0\,\,\left( * \right)\)
Sử dụng MTCT ta tính được phương trình (*) chỉ có 1 nghiệm thỏa mãn t > 0. Với 1 nghiệm t > 0 ta tìm được 2 nghiệm \(x = \pm \sqrt t .\)
Vậy phương trình ban đầu có 2 nghiệm.
Chọn C.
Câu hỏi 15 :
Nếu hai số có tổng bằng – 13 và tích bằng 36 thì số lớn là:
- A - 12
- B -9
- C
-4
- D 2
Đáp án: C
Phương pháp giải:
Hai số có tổng bằng S và tích bằng P là nghiệm của phương trình
\({X^2} - SX + P = 0.\)
Lời giải chi tiết:
Hai số cần tìm là nghiệm của phương trình \({X^2} + 13X + 36 = 0 \Leftrightarrow \left[ \begin{array}{l}X = - 4\\X = - 9\end{array} \right. \Rightarrow \)Số lớn là - 4.
Chọn C.
Câu hỏi 16 :
Tổng các nghiệm của phương trình \(\sqrt 2 {x^2} - 4x + 4 - \sqrt 2 = 0\) bằng:
- A \( - 2\sqrt 2 \)
- B \(\sqrt 2 \)
- C \( - \sqrt 2 \)
- D \(2\sqrt 2 \)
Đáp án: D
Phương pháp giải:
Sử dụng định lí Vi-et để tính tổng các nghiệm của phương trình bậc hai.
Lời giải chi tiết:
Khi phương trình trên có nghiệm thì theo định lí Vi-et ta có: \({x_1} + {x_2} = - \frac{b}{a} = \frac{4}{{\sqrt 2 }} = 2\sqrt 2 .\)
Chọn D.
Câu hỏi 17 :
Gọi \({x_1},{x_2}\) là các nghiệm của phương trình \(4{x^2} - 7x + 1 = 0.\) Khi đó giá trị biểu thức \(M = x_1^2 + x_2^2\) là:
- A \(M = \frac{{57}}{{16}}\)
- B \(M = \frac{{81}}{{64}}\)
- C \(M = \frac{{41}}{{16}}\)
- D \(M = \frac{{41}}{{64}}\)
Đáp án: C
Phương pháp giải:
Phân tích \(M = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\) sau đó áp dụng định lí Vi-et
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\)
Lời giải chi tiết:
Ta có \(\Delta = {7^2} - 4.4.\left( { - 1} \right) > 0 \Rightarrow \) phương trình có 2 nghiệm phân biệt \({x_1},{x_2}\)
Theo định lí Vi-et ta có:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a} = \frac{7}{4}\\{x_1}{x_2} = \frac{c}{a} = \frac{1}{4}\end{array} \right.\)
Ta có: \(M = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {\left( {\frac{7}{4}} \right)^2} - 2\left( { \frac{1}{4}} \right) = \frac{{41}}{{16}}.\)
Chọn C.
Câu hỏi 18 :
Phương trình x2 – m x + 15 = 0 có một nghiệm x1 = 5 thì m và nghiệm x2 còn lại là :
- A x2 = 3 ; m = 10
- B x2 = 12 ; m = 36
- C x2 = -3 ;m = 10
- D x2 = 3 ;m = 8
Đáp án: D
Phương pháp giải:
\(x = {x_0}\) là nghiệm của phương trình \(f\left( x \right) = 0\) thì \(f\left( {{x_0}} \right) = 0.\)
Lời giải chi tiết:
Vì \({x_1} = 5\) là 1 nghiệm của phương trình \( \Rightarrow 25 - 5m + 15 = 0 \Leftrightarrow 5m = 40 \Leftrightarrow m = 8.\)
Khi đó phương trình trở thành:
\({x^2} - 8x + 15 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 3\end{array} \right..\)
Chọn D
Câu hỏi 19 :
Nghiệm của phương trình \(x + \frac{1}{{x - 1}} = \frac{{2x - 1}}{{x - 1}}\)
- A \(x = 0\)
- B \(x = 2\)
- C \(x = 3\)
- D Câu A và B
Đáp án: B
Phương pháp giải:
- Tìm TXĐ
- Quy đồng mẫu thức các phân thức.
- Khử mẫu.
- Giải phương trình tìm nghiệm.
Lời giải chi tiết:
TXĐ: \(D = R\backslash \left\{ 1 \right\}.\)
\(\begin{array}{l}x + \frac{1}{{x - 1}} = \frac{{2x - 1}}{{x - 1}}\\ \Rightarrow x\left( {x - 1} \right) + 1 = 2x - 1\\ \Leftrightarrow {x^2} - x + 1 - 2x + 1 = 0\\ \Leftrightarrow {x^2} - 3x + 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\x = 1\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy nghiệm của phương trình là x = 2.
Chọn B
Câu hỏi 20 :
Tập nghiệm của phương trình \(\left( {{x^2} - x - 2} \right)\sqrt {x - 1} = 0\) là:
- A \(\left[ {1;2} \right]\)
- B \(\left\{ {1;2} \right\}\)
- C \(\left\{ { - 1;1;2} \right\}\)
- D \(\left\{ { - 1;2} \right\}\)
Đáp án: B
Phương pháp giải:
Tìm TXĐ của phương trình sau đó giải phương trình tích.
Lời giải chi tiết:
TXĐ:\(x \ge 1\)
\(\left( {{x^2} - x - 2} \right)\sqrt {x - 1} = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - x - 2 = 0\\\sqrt {x - 1} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 1\\x = 1\end{array} \right..\)
Kết hợp điều kiện xác định ta có tập nghiệm của phương trình là \(\left\{ {1;2} \right\}\).
Chọn B.
Câu hỏi 21 :
Tích các nghiệm của phương trình: \(\sqrt{x+3}-\sqrt{7-x}=\sqrt{2x-8}\) là:
- A -21
- B 28
- C 30
- D -12
Đáp án: C
Phương pháp giải:
+ Phương trình có dạng: \(\sqrt{f(x)}-\sqrt{g(x)}=\sqrt{h(x)}\), điều kiện là \(\left\{ \begin{align} & f(x)\ge 0 \\ & g(x)\ge 0 \\ & h(x)\ge 0 \\\end{align} \right.\)
+ Khi đó: \(\sqrt{f(x)}=\sqrt{h(x)}+\sqrt{g(x)}\Leftrightarrow {{\left( \sqrt{f(x)} \right)}^{2}}={{\left( \sqrt{h(x)}+\sqrt{g(x)} \right)}^{2}}\), giải phương trình ta tìm được x
Lời giải chi tiết:
Điều kiện:
\(\left\{ \begin{array}{l}x + 3 \ge 0\\7 - x \ge 0\\2{\rm{x}} - 8 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\x \le 7\\x \ge 4\end{array} \right. \Leftrightarrow 4 \le x \le 7\)
Khi đó: \(\sqrt{x+3}-\sqrt{7-x}=\sqrt{2x-8}\Leftrightarrow \sqrt{x+3}=\sqrt{2x-8}+\sqrt{7-x}\)
\(\begin{array}{l} \Leftrightarrow x + 3 = 2{\rm{x}} - 8 + 7 - x + 2\sqrt {(2{\rm{x}} - 8)(7 - x)} \\ \Leftrightarrow 2\sqrt {(2{\rm{x}} - 8)(7 - x)} = 4\\ \Leftrightarrow - 2{{\rm{x}}^2} + 22{\rm{x}} - 56 = 4\\ \Leftrightarrow - {x^2} + 11{\rm{x}} - 30 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 5\,\,\,\left( {tm} \right)\\x = 6\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
\(\Rightarrow\) Tích của 2 nghiệm bằng 30
Chọn C.
Câu hỏi 22 :
Số nghiệm của phương trình \(\left( {{x^4} - 11{x^2} + 18} \right)\sqrt {x + 2} = 0\) là:
- A 2
- B 5
- C 3
- D 4
Đáp án: D
Phương pháp giải:
Tìm TXĐ của phương trình sau đó giải phương trình tích.
Lời giải chi tiết:
- TXĐ: \(x \ge - 2.\)
\(\begin{array}{l}\left( {{x^4} - 11{x^2} + 18} \right)\sqrt {x + 2} = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^4} - 11{x^2} + 18 = 0\\\sqrt {x + 2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left( {{x^2} - 9} \right)\left( {{x^2} - 2} \right) = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} - 9 = 0\\{x^2} - 2 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pm 3\\x = \pm \sqrt 2 \\x = - 2\end{array} \right..\end{array}\)
Kết hợp điều kiện ta có
\(\left[ \begin{array}{l}x = 3\\x = \pm \sqrt 2 \\x = - 2\end{array} \right.\)
Vậy phương trình đã cho có 4 nghiệm.
Chọn D.
Câu hỏi 23 :
Phương trình \({x^2} + 5x - 9 = 0\) có tổng bình phương hai nghiệm là:
- A 19
- B 15
- C 43
- D 40
Đáp án: C
Phương pháp giải:
Cách 1: Tính trực tiếp hai nghiệm của phương trình bậc hai rồi tính tổng bình phương của 2 nghiệm đó.
Cách 2: Áp dụng định lí Vi-et: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}.\)
Lời giải chi tiết:
Vì ac = -9 < 0 nên phương trình luôn có 2 nghiệm trái dấu.
Gọi hai nghiệm của phương trình là \({x_1},{x_2}\).
Theo định lí Vi-et ta có:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - 5\\{x_1}{x_2} = - 9\end{array} \right.\)
Ta có: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {\left( { - 5} \right)^2} - 2.\left( { - 9} \right) = 25 + 18 = 43.\)
Chọn C.
Câu hỏi 24 :
Tổng hai nghiệm của phương trình \(5\sqrt x + \dfrac{5}{{2\sqrt x }} = 2{\rm{x}} + \dfrac{1}{{2{\rm{x}}}} + 4\) là:
- A 4
- B 3
- C \(\dfrac{1}{4}\)
- D -3
Đáp án: B
Phương pháp giải:
Đặt: \(\sqrt x + \dfrac{1}{{2\sqrt x }} = t\,\,(t \ge 0) \Leftrightarrow {\left( {\sqrt x + \dfrac{1}{{2\sqrt x }}} \right)^2} = {t^2}\) ta được phương trình bậc 2 ẩn t
Lời giải chi tiết:
Điều kiện: \(x > 0\)
Ta có: \(5\sqrt x + \dfrac{5}{{2\sqrt x }} = 2{\rm{x}} + \dfrac{1}{{2{\rm{x}}}} + 4 \Leftrightarrow 5\left( {\sqrt x + \dfrac{1}{{2\sqrt x }}} \right) = 2\left( {{\rm{x}} + \dfrac{1}{{{\rm{4x}}}}} \right) + 4\)
Đặt \(\sqrt x + \dfrac{1}{{2\sqrt x }} = t\,\,\,\left( {t > 0} \right) \Leftrightarrow {t^2} = x + \dfrac{1}{{4x}} + 1 \Leftrightarrow x + \dfrac{1}{{4x}} = {t^2} - 1\)
Khi đó phương trình trở thành: \(5t = 2\left( {{t^2} - 1} \right) + 4 \Leftrightarrow 2{t^2} - 5t + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 2\,\,\,\left( {tm} \right)\\t = \dfrac{1}{2}\,\,\,\left( {tm} \right)\end{array} \right.\)
+) Với \(t = \dfrac{1}{2} \Leftrightarrow x + \dfrac{1}{{4{\rm{x}}}} = - \dfrac{3}{4} \Leftrightarrow 4{{\rm{x}}^2}{\rm{ + 3x}} + 1 = 0\) (vô nghiệm)
+) Với t = 2\( \Leftrightarrow x + \dfrac{1}{{4{\rm{x}}}} = 3 \Leftrightarrow 4{{\rm{x}}^2} - 12{\rm{x}} + 1 = 0\)
Tổng 2 nghiệm của phương trình là: 3
Chọn B.
Câu hỏi 25 :
Cho phương trình \(2{{\rm{x}}^2} + 3{\rm{x}} - 14 = 2\sqrt[3]{{2{{\rm{x}}^2} + 3{\rm{x}} - 10}}\) . Giả sử x1, x2 là 2 nghiệm của phương trình. Tính giá trị biểu thức \(A = \sqrt {{x_1}^2 + {x_2}^2 - 4{{\rm{x}}_1}.{x_2}} \)
- A \(2\)
- B \(\dfrac{{225}}{4}\)
- C
\(\dfrac{3}{4}\)
- D \(\dfrac{{15}}{2}\)
Đáp án: D
Phương pháp giải:
+ Đặt \(t = \sqrt[3]{{2{{\rm{x}}^2} + 3{\rm{x}} - 10}}\) suy ra phương trình bậc 3 với ẩn t
+ Tính giá trị biểu thức A bằng cách sử dụng định lý Vi – et
Lời giải chi tiết:
Đặt \(t = \sqrt[3]{{2{{\rm{x}}^2} + 3{\rm{x}} - 10}} \Leftrightarrow {t^3} = 2{{\rm{x}}^2} + 3{\rm{x}} - 10 \Leftrightarrow {t^3} + 10 = 2{{\rm{x}}^2} + 3{\rm{x}}\)
Khi đó phương trình trở thành: \({t^3} + 10 - 14 = 2t \Leftrightarrow {t^3} - 2t - 4 = 0\) \( \Leftrightarrow \left( {t - 2} \right)\left( {{t^2} + 2t + 2} \right) = 0 \Leftrightarrow t = 2\) (Vì \({t^2} + 2t + 2\) = 0 vô nghiệm)
+) Với t = 2 \( \Leftrightarrow 2{{\rm{x}}^2} + 3x = 18 \Leftrightarrow 2{{\rm{x}}^2} + 3x - 18 = 0\,\,\left( * \right)\,\,\,\left( {tm} \right)\)
Giả sử x1, x2 là hai nghiệm của phương trình (*)
Theo Vi – et, ta có : \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{3}{2}\\{x_1}.{x_2} = - 9\end{array} \right.\)
\( \Rightarrow A = \sqrt {{x_1}^2 + {x_2}^2 - 4{{\rm{x}}_1}{x_2}} = \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 6{x_1}.{x_2}} = \sqrt {\dfrac{9}{4} + 54} = \sqrt {\dfrac{{225}}{4}} = \dfrac{{15}}{2}\)
Chọn D.
Câu hỏi 26 :
Tập nghiệm của phương trình \(4{x^2} + 5{\rm{x}} = 2\sqrt {x + 2} - 4\) là:
- A \(\left\{ \emptyset \right\}\)
- B \(\left\{ { - \dfrac{1}{2}} \right\}\)
- C {-2}
- D {-1}
Đáp án: A
Phương pháp giải:
+ Đưa phương trình về dạng : \({A^2} + {B^2} = 0\)
+ Phương trình có nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\).
Giải hệ phương trình ta tìm được x
Lời giải chi tiết:
Điều kiện: \(x + 2 \ge 0 \Leftrightarrow x \ge - 2\)
Phương trình: \(4{x^2} + 5{\rm{x}} = 2\sqrt {x + 2} - 4 \Leftrightarrow 4{x^2} + 5x - 2\sqrt {x + 2} + 4 = 0\)
\(\begin{array}{l} \Leftrightarrow \left( {4{x^2} + 4x + 1} \right) + \left( {x + 2 - 2\sqrt {x + 2} + 1} \right) = 0\\ \Leftrightarrow {\left( {2{\rm{x}} + 1} \right)^2} + {\left( {\sqrt {x + 2} - 1} \right)^2} = 0\end{array}\)
Ta có:\({\left( {2{\rm{x}} + 1} \right)^2} \ge 0,{\left( {\sqrt {x + 2} - 1} \right)^2} \ge 0,\forall x \ge - 2\)
Để \({\left( {2{\rm{x}} + 1} \right)^2} + {\left( {\sqrt {x + 2} - 1} \right)^2} = 0\)
Thì: \(\left\{ \begin{array}{l}{\left( {2{\rm{x}} + 1} \right)^2} = 0\\{\left( {\sqrt {x + 2} - 1} \right)^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{\rm{x}} + 1 = 0\\\sqrt {x + 2} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{1}{2}\\x = - 1\end{array} \right.\) (vô lý)
Vậy phương trình vô nghiệm.
Chọn A.
Câu hỏi 27 :
Số nghiệm nguyên của phương trình \(\sqrt{5\text{x}-3}+\sqrt{3\text{x}-1}=x-1\) là:
- A 0
- B 1
- C 2
- D 3
Đáp án: A
Phương pháp giải:
+ Phương trình có dạng: \(\sqrt{f(x)}+\sqrt{g(x)}=h(x)\), điều kiện là \(\left\{ \begin{align} & f(x)\ge 0 \\ & g(x)\ge 0 \\ & h(x)\ge 0 \\\end{align} \right.\)
+ Khi đó: \({{\left( \sqrt{f(x)}+\sqrt{g(x)} \right)}^{2}}={{h}^{2}}(x)\), giải phương trình ta tìm được x
Lời giải chi tiết:
Điều kiện:
\(\left\{ \begin{array}{l}5x - 3 \ge 0\\3x - 1 \ge 0\\x - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{3}{5}\\x \ge \frac{1}{3}\\x \ge 1\end{array} \right. \Leftrightarrow x \ge 1\)
Phương trình \(\Leftrightarrow 5\text{x}-3+3\text{x}-1+2\sqrt{(5\text{x}-3)(3\text{x}-1)}={{x}^{2}}-2\text{x}+1\)
\(\Leftrightarrow 2\sqrt{(5\text{x}-3)(3\text{x}-1)}={{x}^{2}}-10\text{x}+5\)
Điều kiện : \({{x}^{2}}-10\text{x}+5\ge 0\Leftrightarrow \left[ \begin{align} & x\ge 5+2\sqrt{5} \\& x\le 5-2\sqrt{5} \\\end{align} \right.\)
Phương trình
\(\begin{array}{l} \Leftrightarrow 4\left( {15{{\rm{x}}^2} - 14{\rm{x}} + 3} \right) = {\left( {{x^2} - 10{\rm{x}} + 5} \right)^2}\\ \Leftrightarrow 60{x^2} - 56x + 12 = {x^4} + 100{x^2} + 25 - 20{x^3} + 10{x^2} - 100x\\ \Leftrightarrow {x^4} - 20{{\rm{x}}^3} + 50{{\rm{x}}^2} - 44{\rm{x}} + 13 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2}\left( {{x^2} - 18{\rm{x}} + 13} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(ktm)\\x = 9 \pm 2\sqrt {17} \notin Z\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy phương trình không có nghiệm nguyên.
Chọn A
Câu hỏi 28 :
a) Tìm m để phương trình \({x^2} + 2x + m = 0\) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa \(x_1^2 + x_2^2 = 6\).
b) Giải phương trình: \(\sqrt {{x^2} + 2x - 6} = 2x - 3\).
- A a)\(m = - 1\).
b) \(S = \left\{ {3;\frac{5}{3}} \right\}\).
- B a)\(m = - 2\).
b) \(S = \left\{ {3;\frac{5}{3}} \right\}\).
- C a)\(m = - 1\).
b) \(S = \left\{ {3;\frac{7}{3}} \right\}\).
- D a)\(m = - 1\).
b) \(S = \left\{ {3;\frac{11}{3}} \right\}\).
Đáp án: A
Phương pháp giải:
a)Sử dụng hệ thức Vi-ét.
b)\(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\).
Lời giải chi tiết:
a)Để phương trình \({x^2} + 2x + m = 0\) có 2 nghiệm phân biệt thì \(\Delta ' > 0 \Leftrightarrow 1 - m > 0 \Leftrightarrow m < 1\)
Theo Vi – ét, ta có: \({x_1} + {x_2} = \frac{{ - 2}}{1} = - 2,\,\,\,{x_1}{x_2} = \frac{m}{1} = m\)
Theo đề bài: \(x_1^2 + x_2^2 = 6 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 6 \Leftrightarrow {\left( { - 2} \right)^2} - 2m = 6 \Leftrightarrow 4 - 2m = 6 \Leftrightarrow 2m = - 2 \Leftrightarrow m = - 1\) (thỏa mãn)
Kết luận: \(m = - 1\).
b) \(\begin{array}{l}\sqrt {{x^2} + 2x - 6} = 2x - 3 \Leftrightarrow \left\{ \begin{array}{l}2x - 3 \ge 0\\{x^2} + 2x - 6 = {\left( {2x - 3} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{3}{2}\\{x^2} + 2x - 6 = 4{x^2} - 12x + 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{3}{2}\\3{x^2} - 14x + 15 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \frac{5}{3}\end{array} \right.\,\,\left( {tm} \right)\end{array}\)
Vậy, phương trình đã cho có tập nghiệm \(S = \left\{ {3;\frac{5}{3}} \right\}\).
Câu hỏi 29 :
Số nghiệm nguyên của phương trình: \(\sqrt {x - 3} + 5 = \sqrt {7 - x} + x\) là:
- A 3
- B 0
- C 1
- D 2
Đáp án: A
Phương pháp giải:
Sử dụng biểu thức liên hợp.
Lời giải chi tiết:
ĐKXĐ: \(\left\{ \begin{array}{l}x - 3 \ge 0\\7 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x \le 7\end{array} \right. \Leftrightarrow 3 \le x \le 7 \Rightarrow \)Tập xác định \(D = \left[ {3;7} \right]\)
\(\begin{array}{l}\sqrt {x - 3} + 5 = \sqrt {7 - x} + x \Leftrightarrow \sqrt {x - 3} - \sqrt {7 - x} = x - 5 \Leftrightarrow \frac{{\left( {\sqrt {x - 3} - \sqrt {7 - x} } \right)\left( {\sqrt {x - 3} + \sqrt {7 - x} } \right)}}{{\sqrt {x - 3} + \sqrt {7 - x} }} = x - 5\\ \Leftrightarrow \frac{{2x - 10}}{{\sqrt {x - 3} + \sqrt {7 - x} }} = x - 5 \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\\frac{2}{{\sqrt {x - 3} + \sqrt {7 - x} }} = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\,\,(TM)\\\sqrt {x - 3} + \sqrt {7 - x} = 2\,\,(1)\end{array} \right.\end{array}\),
\(\left( 1 \right) \Leftrightarrow x - 3 + 2\sqrt {\left( {x - 3} \right)\left( {7 - x} \right)} + 7 - x = 4 \Leftrightarrow 2\sqrt {\left( {x - 3} \right)\left( {7 - x} \right)} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 7\end{array} \right.\,\,\,\,\left( {TM} \right)\)
Vậy phương trình đã cho có 3 nghiệm nguyên là \(x = 3,\,\,x = 5,\,\,x = 7\).
Chọn: A
Câu hỏi 30 :
Tìm m để phương trình \({x^2} - \left( {2m + 1} \right)x + {m^2} + 1 = 0\) có 2 nghiệm \({x_1};{x_2}\) thỏa mãn \({x_2} = 2{x_1}\)
- A \(m = 1;\,\,m = 7\)
- B \(m = 2;\,\,m = 7\)
- C \(m = 1;\,\,m = 5\)
- D \(m = 1;\,\,m = 0\)
Đáp án: A
Phương pháp giải:
+) Tìm điều kiện để phương trình có 2 nghiệm.
+) Sử dụng hệ thức Vi-ét.
Lời giải chi tiết:
Ta có:
\(\begin{gathered} \Delta = {\left( {2m + 1} \right)^2} - 4\left( {{m^2} + 1} \right) \hfill \\ \Delta = 4{m^2} + 4m + 1 - 4{m^2} - 4 = 4m - 3 \hfill \\ \end{gathered} \)
Để phương trình có 2 nghiệm \({x_1};{x_2} \Leftrightarrow \Delta \geqslant 0 \Leftrightarrow 4m - 3 \geqslant 0 \Leftrightarrow m \geqslant \frac{3}{4}\)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{gathered} {x_1} + {x_2} = 2m + 1 \hfill \\ {x_1}{x_2} = {m^2} + 1 \hfill \\ \end{gathered} \right.\)
Để 2 nghiệm \({x_1};{x_2}\) thỏa mãn \({x_2} = 2{x_1}\) ta có:
\(\left\{ \begin{gathered} {x_1} + {x_2} = 2m + 1 \hfill \\ {x_1}{x_2} = {m^2} + 1 \hfill \\ {x_2} = 2{x_1} \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} 3{x_1} = 2m + 1 \hfill \\ 2x_1^2 = {m^2} + 1 \hfill \\ {x_2} = 2{x_1} \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} {x_1} = \frac{{2m + 1}}{3} \hfill \\ {x_2} = \frac{{2\left( {2m + 1} \right)}}{3} \hfill \\ 2.\frac{{{{\left( {2m + 1} \right)}^2}}}{9} = {m^2} + 1\,\,\left( * \right) \hfill \\ \end{gathered} \right.\)
Giải (*): \(\frac{{2{{\left( {2m + 1} \right)}^2}}}{9} = {m^2} + 1 \Leftrightarrow 2\left( {4{m^2} + 4m + 1} \right) = 9\left( {{m^2} + 1} \right) \Leftrightarrow {m^2} - 8m + 7 = 0 \Leftrightarrow \left[ \begin{gathered} m = 1 \hfill \\ m = 7 \hfill \\ \end{gathered} \right.\,\,\left( {tm} \right)\)
Vậy \(m = 1;\,\,m = 7\)
Câu hỏi 31 :
Cho phương trình \(\frac{{3m\left( {x - 1} \right)}}{{x + 1}} = 5m + 1\). Khẳng định nào dưới đây đúng?
- A Khi \(m \ne - \frac{1}{8}\) phương trình có nghiệm bằng 0.
- B Khi \(m \ne - \frac{1}{2}\) phương trình có nghiệm duy nhất \(x = \frac{{ - 8m - 1}}{{2m + 1}}\).
- C Khi \(\left\{ \begin{array}{l}m \ne - \frac{1}{2}\\m \ne 0\end{array} \right.\) phương trình có nghiệm duy nhất \(x = \frac{{ - 8m - 1}}{{2m + 1}}\).
- D Khi \(m = - \frac{1}{2}\) phương trình có tập nghiệm bằng \(S = \mathbb{R}\).
Đáp án: C
Phương pháp giải:
Xét phương trình dạng \(a\,x = b\) (1):
+) Nếu \(a \ne 0\) thì (1) có nghiệm duy nhất \(x = \frac{b}{a}\)
+) Nếu \(a = b = 0\) thì (1) có vô số nghiệm
+) Nếu \(a = 0,\,\,b \ne 0\) thì (1) vô nghiệm.
Lời giải chi tiết:
ĐKXĐ: \(x \ne - 1\)
\(\begin{array}{l}\frac{{3m\left( {x - 1} \right)}}{{x + 1}} = 5m + 1\,\,\,(*) \Leftrightarrow 3m\left( {x - 1} \right) = \left( {5m + 1} \right)\left( {x + 1} \right) \Leftrightarrow 3mx - 3m = 5mx + 5m + x + 1\\ \Leftrightarrow \left( {2m + 1} \right)x = - 8m - 1\,\,(2*)\end{array}\)
+) TH1: \(2m + 1 = 0 \Leftrightarrow m = - \frac{1}{2}\):
\(\left( {2*} \right) \Leftrightarrow 0x = - \frac{3}{4}\) (vô nghiệm) \( \Rightarrow \) Phương trình (*) vô nghiệm.
+) TH2: \(2m + 1 \ne 0 \Leftrightarrow m \ne - \frac{1}{2}\):
\(\left( {2*} \right) \Leftrightarrow x = \frac{{ - 8m - 1}}{{2m + 1}}\)
Xét \(\frac{{ - 8m - 1}}{{2m + 1}} = - 1 \Leftrightarrow 8m + 1 = 2m + 1 \Leftrightarrow m = 0\)
\( \Rightarrow \) Với \(m = 0\): phương trình (*) vô nghiệm; với \(m \ne 0\), phương trình (*) có nghiệm duy nhất \(x = \frac{{ - 8m - 1}}{{2m + 1}}\).
Chọn: C
Câu hỏi 32 :
Cho phương trình \(\left| {x - 3m + 1} \right| = \left| {\left( {m + 1} \right)x - 3} \right|\). Khẳng định nào dưới đây đúng?
- A Khi \(m = 0\) phương trình vô nghiệm.
- B Khi \(m = - 2\) phương trình có nghiệm duy nhất.
- C Khi \(m \ne 0\) và \(m \ne - 2\) phương trình có hai nghiệm.
- D Khi \(m \ne 0\) phương trình có nghiệm duy nhất.
Đáp án: B
Phương pháp giải:
Xét phương trình dạng \(a\,x = b\) (1):
+) Nếu \(a \ne 0\) thì (1) có nghiệm duy nhất \(x = \frac{b}{a}\)
+) Nếu \(a = b = 0\) thì (1) có vô số nghiệm
+) Nếu \(a = 0,\,\,b \ne 0\) thì (1) vô nghiệm.
Lời giải chi tiết:
\(\left| {x - 3m + 1} \right| = \left| {\left( {m + 1} \right)x - 3} \right|\,\,\,\,\,\,(*)\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x - 3m + 1 = \left( {m + 1} \right)x - 3\\x - 3m + 1 = - \left( {m + 1} \right)x + 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}mx = - 3m + 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\\left( {m + 2} \right)x = 3m + 2\,\,\,\,\,\,(2)\end{array} \right.\)
+) \(m = 0\):
\( - 3m + 4 = 4 \ne 0 \Rightarrow \) Phương trình (1) vô nghiệm
\((2) \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\): Phương trình (2) có nghiệm duy nhất \(x = 1\)
Vậy, với \(m = 0\) phương trình đã cho có nghiệm duy nhất \(x = 1\).
+) \(m = - 2\):
\((1) \Leftrightarrow - 2x = 10 \Leftrightarrow x = - 5\): Phương trình (1) có nghiệm duy nhất \(x = - 5\)
\((2) \Leftrightarrow 0x = - 4\): Vô nghiệm
Vậy, với \(m = - 2\) phương trình đã cho có nghiệm duy nhất \(x = - 5\).
+) \(m \ne 0\) và \(m \ne - 2\)
\(\left( 1 \right) \Leftrightarrow x = \frac{{ - 3m + 4}}{m};\,\,\,\,\,\left( 2 \right) \Leftrightarrow \frac{{3m + 2}}{{m + 2}}\)
Xét \(\frac{{ - 3m + 4}}{m} = \frac{{3m + 2}}{{m + 2}}\)\(\begin{array}{l} \Leftrightarrow \left( { - 3m + 4} \right)\left( {m + 2} \right) = \left( {3m + 2} \right)m \Leftrightarrow - 3{m^2} - 2m + 8 = 3{m^2} + 2m \Leftrightarrow 6{m^2} + 4m - 8 = 0 \Leftrightarrow 3{m^2} + 2m - 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = \frac{{ - 1 + \sqrt {13} }}{3}\\m = \frac{{ - 1 - \sqrt {13} }}{3}\end{array} \right.\end{array}\)\( \Rightarrow \frac{{3m - 4}}{m} \ne \frac{{3m + 2}}{{m + 2}},\,\,\forall m \ne 0,\,m \ne - 2,\,m \ne \frac{{ - 1 \pm \sqrt {13} }}{3}\)
Vậy, với \(m \ne 0\), \(m \ne - 2\) và \(\,m \ne \frac{{ - 1 \pm \sqrt {13} }}{3}\) phương trình đã cho có 2 nghiệm phân biệt. Với \(\,m = \frac{{ - 1 \pm \sqrt {13} }}{3}\), phương trình có nghiệm duy nhất.
Chọn: B
Câu hỏi 33 :
Gọi n là số các giá trị của tham số m để phương trình \(\frac{{\left( {x + 1} \right)\left( {mx + 2} \right)}}{{x - 2}} = 0\) có nghiệm duy nhất. Khi đó n là :
- A 2
- B 1
- C 0
- D 3
Đáp án: D
Phương pháp giải:
Giải phương trình tích.
TH1 : \(m = 0\)
TH2: \(m \ne 0\), phương trình có nghiệm duy nhất khi phương trình tử có nghiệm kép hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm không thỏa mãn ĐK của bài toán.
Lời giải chi tiết:
ĐK : \(x \ne 2\)
\(\frac{{\left( {x + 1} \right)\left( {mx + 2} \right)}}{{x - 2}} = 0 \Leftrightarrow \left[ \begin{gathered} x = - 1\,\,\,\left( {tm} \right) \hfill \\ mx + 2 = 0\,\,\,\left( * \right) \hfill \\ \end{gathered} \right.\)
Giải (*)
TH1 : \(m = 0 \Rightarrow 0x + 2 = 0\) (Vô nghiệm) \( \Rightarrow \) Phương trình ban đầu có nghiệm duy nhất \(x = - 1\).
\( \Rightarrow m = 0\) thỏa mãn.
TH2 : \(m \ne 0 \Rightarrow \left( * \right) \Leftrightarrow x = \frac{{ - 2}}{m}\)
Để phương trình ban đầu có nghiệm duy nhất \( \Leftrightarrow \left[ \begin{gathered} -\frac{2}{m} = - 1 \hfill \\ - \frac{2}{m} = 2 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m = 2 \hfill \\ m = - 1 \hfill \\ \end{gathered} \right.\)
Vậy \(m \in \left\{ {0; - 1;2} \right\}\). Khi đó \(n = 3\).
Chọn đáp án D.
Câu hỏi 34 :
Xác định \(m\) để phương trình \({x^2} + 1 = mx\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa \({x_1} - {x_2} = 1\) (giả sử \({x_1} > {x_2}\)).
- A \(m = \pm \sqrt 5 \).
- B \(m = \pm \sqrt 2 \).
- C \(m = \pm \sqrt 7 \).
- D \(m = \pm \sqrt 11 \).
Đáp án: A
Phương pháp giải:
Phương trình có 2 nghiệm phân biệt \( \Leftrightarrow \Delta > 0\).
Sử dụng hệ thức Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\).
Lời giải chi tiết:
\({x^2} + 1 = mx \Leftrightarrow {x^2} - mx + 1 = 0\)
Để phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta = {m^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < - 2\end{array} \right.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = 1\end{array} \right.\)
Ta có:
\(\begin{array}{l}{x_1} - {x_2} = 1 \Rightarrow {\left( {{x_1} - {x_2}} \right)^2} = 1 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 1\\ \Leftrightarrow {m^2} - 4 = 1 \Leftrightarrow {m^2} = 5 \Leftrightarrow m = \pm \sqrt 5 \,\,\left( {tm} \right)\end{array}\)
Vậy \(m = \pm \sqrt 5 \).
Câu hỏi 35 :
Tìm tất cả các giá trị của m để phương trình \({x^2} - \left( {2m + 1} \right)x + {m^2} + 2 = 0\) có hai nghiệm \({x_1};{x_2}\) phân biệt sao cho \({x_1}\left( {{x_2} - 2{x_1}} \right) + {x_2}\left( {{x_1} - 2{x_2}} \right) + 14 = 0\).
- A \(m=2\)
- B \(m=2; \,\, m=-6\)
- C \(m=-6\)
- D Không tồn tại \(m\) thỏa mãn
Đáp án: A
Phương pháp giải:
+) Tìm điều kiện để phương trình có 2 nghiệm phân biệt.
+) Áp dụng định lí Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Lời giải chi tiết:
Để phương trình có 2 nghiệm phân biệt \({x_1};{x_2}\)\( \Leftrightarrow \Delta > 0\)
\( \Leftrightarrow {\left( {2m + 1} \right)^2} - 4\left( {{m^2} + 2} \right) > 0 \Leftrightarrow 4{m^2} + 4m + 1 - 4{m^2} - 8 > 0 \Leftrightarrow 4m - 7 > 0 \Leftrightarrow m > \dfrac{7}{4}\).
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = {m^2} + 2\end{array} \right.\)
\(\begin{array}{l}\,\,\,\,\,{x_1}\left( {{x_2} - 2{x_1}} \right) + {x_2}\left( {{x_1} - 2{x_2}} \right) + 14 = 0\\ \Leftrightarrow {x_1}{x_2} - 2x_1^2 + {x_1}{x_2} - 2x_2^2 + 14 = 0\\ \Leftrightarrow 2{x_1}{x_2} - 2\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] + 14 = 0\\ \Leftrightarrow - 2{\left( {{x_1} + {x_2}} \right)^2} + 6{x_1}{x_2} + 14 = 0\\ \Leftrightarrow - 2{\left( {2m + 1} \right)^2} + 6\left( {{m^2} + 2} \right) + 14 = 0\\ \Leftrightarrow - 8{m^2} - 8m - 2 + 6{m^2} + 12 + 14 = 0\\ \Leftrightarrow - 2{m^2} - 8m + 24 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\,\,\,\,\left( {tm} \right)\\m = - 6\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy \(m = 2.\)
Câu hỏi 36 :
Số nghiệm của phương trình \({x^2} + 3x + 1 = \left( {x + 3} \right)\sqrt {{x^2} + 1} \) là
- A 3
- B 1
- C 4
- D 2
Đáp án: D
Phương pháp giải:
Đặt \(\sqrt {{x^2} + 1} = t\).
Lời giải chi tiết:
\({x^2} + 3x + 1 = \left( {x + 3} \right)\sqrt {{x^2} + 1} \,\,\,\left( {D = R} \right)\).
Đặt \(\sqrt {{x^2} + 1} = t\), \(t \ge 1\), phương trình trở thành:
\({t^2} + 3x = \left( {x + 3} \right)t \Leftrightarrow {t^2} + 3x = xt + 3t \Leftrightarrow t\left( {x - t} \right) + 3\left( {x - t} \right) = 0 \Leftrightarrow \left( {x - t} \right)\left( {t - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = t\\t = 3\end{array} \right.\)
+) \(x = t \Rightarrow x = \sqrt {{x^2} + 1} \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = {x^2} + 1\end{array} \right. \Leftrightarrow x \in \emptyset \)
+) \(t = 3 \Rightarrow \sqrt {{x^2} + 1} = 3 \Leftrightarrow {x^2} = 8 \Leftrightarrow x = \pm 2\sqrt 2 \)
\( \Rightarrow \) Số nghiệm của phương trình là 2.
Chọn: D
Câu hỏi 37 :
Giải phương trình \(\sqrt {2{x^2} - 5x + 2} = x - 2\)
- A \(x=2;x=-1\)
- B \(x=2\)
- C \(x=-1\)
- D Vô nghiệm
Đáp án: B
Phương pháp giải:
\(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\)
Lời giải chi tiết:
\(\sqrt {2{x^2} - 5x + 2} = x - 2 \Leftrightarrow \left\{ \begin{array}{l}x - 2 \ge 0\\2{x^2} - 5x + 2 = {x^2} - 4x + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\{x^2} - x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x = 2\\x = - 1\end{array} \right.\end{array} \right. \Leftrightarrow x = 2\)
Vậy phương trình có nghiệm duy nhất \(x = 2\).
Câu hỏi 38 :
Tìm m để phương trình \(\frac{{2\left( {2 - 2m - x} \right)}}{{x + 1}} = x - 2m\) có 2 nghiệm phân biệt ?
- A \(m \ne \frac{5}{2}\) và \(m \ne 1\)
- B \(m \ne \frac{5}{2}\) và \(m \ne \frac{3}{2}\)
- C \(m \ne \frac{5}{2}\) và \(m \ne \frac{1}{2}\)
- D \(m \ne \frac{5}{2}\)
Đáp án: B
Phương pháp giải:
+) Tìm ĐKXĐ.
+) Quy đồng bỏ mẫu, đưa phương trình về dạng phương trình bậc hai.
+) Tìm điều kiện để phương trình bậc hai đó có 2 nghiệm phân biệt thỏa mãn ĐKXĐ.
Lời giải chi tiết:
ĐK : \(x \ne - 1\)
\(\begin{array}{l}pt \Leftrightarrow 4 - 4m - 2x = {x^2} - 2mx + x - 2m\\ \Leftrightarrow {x^2} + \left( {3 - 2m} \right)x + 2m - 4 = 0\,\,\left( * \right)\end{array}\)
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm phân biệt khác 1.
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\left( {3 - 2m} \right)^2} - 4\left( {2m - 4} \right) > 0\\1 - 3 + 2m + 2m - 4 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 20m + 25 > 0\\4m - 6 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {2m - 5} \right)^2} > 0\\m \ne \frac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m - 5 \ne 0\\m \ne \frac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \frac{5}{2}\\m \ne \frac{3}{2}\end{array} \right.\end{array}\)
Vậy \(m \ne \frac{5}{2}\) và \(m \ne \frac{3}{2}\).
Chọn đáp án B.
Câu hỏi 39 :
Tìm m để parabol \(\left( P \right):\,\,y = {x^2} - 2\left( {m + 1} \right)x + {m^2} - 3\) cắt trục hoành tại 2 điểm phân biệt có hoành độ \({x_1};{x_2}\) sao cho \({x_1}{x_2} = 1\).
- A \(m = 2\)
- B Không tồn tại m
- C \(m = - 2\)
- D \(m = \pm 2\)
Đáp án: A
Phương pháp giải:
+) Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình hoành độ giao điểm có 2 nghiệm phân biệt.
+) Sử dụng hệ thức Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm: \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 3 = 0\,\,\left( * \right)\).
Để (P) cắt trục hoành tại 2 điểm phân biệt có hoành độ \({x_1};{x_2}\)thì phương trình (*) có 2 nghiệm phân biệt.
Ta có \(\Delta ' = {\left( {m + 1} \right)^2} - {m^2} + 3 = 2m + 4 > 0 \Leftrightarrow m > - 2\).
Khi đó theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 2\\{x_1}{x_2} = {m^2} - 3\end{array} \right.\)
Theo đề bài ta có \({x_1}{x_2} = 1 \Leftrightarrow {m^2} - 3 = 1 \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\left( {tm} \right)\\m = - 2\,\,\left( {ktm} \right)\end{array} \right.\)
Chọn đáp án A.
Câu hỏi 40 :
Một xe hơi khởi hành từ Krông Năng đi đến Nha Trang cách nhau \({\rm{175}}\)km. Khi về xe tăng vận tốc trung bình hơn vận tốc trung bình lúc đi là \(20\)km/giờ. Biết rằng thời gian dùng để đi và về là \(6\)giờ; vận tốc trung bình lúc đi là:
- A \(60\) km/giờ.
- B \(45\) km/giờ.
- C \(55\) km/giờ.
- D \(50\) km/giờ.
Đáp án: D
Phương pháp giải:
Giải bài toán bằng cách lập phương trình.
Lời giải chi tiết:
Gọi vận tốc trung bình lúc đi là x (km/h) \(\left( {x > 0} \right)\) thì vận tốc trung bình lúc về là \(x + 20\,\,\left( {km/h} \right)\).
Thời gian lúc đi và lúc về lần lượt là \(\dfrac{{175}}{x};\dfrac{{175}}{{x + 20}}\) (h).
Vì thời gian dùng để đi và về là 6h nên ta có phương trình: \(\dfrac{{175}}{x} + \dfrac{{175}}{{x + 20}} = 6\)
\( \Leftrightarrow 175\left( {x + 20} \right) + 175x = 6x\left( {x + 20} \right) \Leftrightarrow 6{x^2} - 230x - 3500 = 0 \Leftrightarrow x = 50\).
Vậy vận tốc trung bình lúc đi là 50 km/h.
Chọn D.
Câu hỏi 41 :
Tìm \(m\) để phương trình \(m{x^2}--2\left( {m + 1} \right)x + m + 1 = 0\) vô nghiệm.
- A \(m < - 1\).
- B \(m \le 1\) hoặc \(m \ge 0\).
- C \(m = 0\)và \(m < - 1\).
- D \(m = 0\)và \(m > - 1\).
Đáp án: A
Phương pháp giải:
TH1: \(m = 0\), thay vào tìm nghiệm của phương trình.
TH2: \(m \ne 0\), phương trình vô nghiệm \( \Leftrightarrow \Delta ' < 0\).
Lời giải chi tiết:
TH1: \(m = 0\), phương trình trở thành \( - 2x + 1 = 0 \Leftrightarrow x = \dfrac{1}{2}\). Suy ra \(m = 0\) không thỏa mãn.
TH2: \(m \ne 0\). Khi đó phương trình vô nghiệm \( \Leftrightarrow \Delta ' < 0\)
\( \Leftrightarrow {\left( {m + 1} \right)^2} - m\left( {m + 1} \right) < 0 \Leftrightarrow {m^2} + 2m + 1 - {m^2} - m = m + 1 < 0 \Leftrightarrow m < - 1\).
Chọn A.
Câu hỏi 42 :
Tìm tất cả các giá trị của m để phương trình \({x^2} - \left( {m + 1} \right)x + m = 0\) có hai nghiệm phân biệt và nghiệm này bằng một nửa nghiệm kia.
- A \(m = \frac{1}{2};m = \frac{1}{3}\)
- B \(m = \frac{1}{2};m = - 3\)
- C \(m = 2;m = \frac{1}{2}\)
- D \(m = 2;m = - 3\)
Đáp án: C
Phương pháp giải:
Phương trình bậc 2 có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0\). Kết hợp với hệ thức Vi-ét và dữ kiện đề bài để tìm m.
Lời giải chi tiết:
\({x^2} - \left( {m + 1} \right)x + m = 0\) (1)
Có : \(\Delta = {\left( {m + 1} \right)^2} - 4m = {\left( {m - 1} \right)^2}\)
Để phương trình (1) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0 \Leftrightarrow m - 1 \ne 0 \Leftrightarrow m \ne 1\)
Gọi \({x_1} > {x_2}\) là 2 nghiệm của (1)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 1\\{x_1}.{x_2} = m\end{array} \right.\)
Mặt khác theo đề bài: \({x_1} = 2{x_2} \Rightarrow \left\{ \begin{array}{l}2{x_2} + {x_2} = m + 1\\2{x_2}.{x_2} = m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = \frac{{m + 1}}{3}\\2{x_2}^2 = m\end{array} \right.\)
\( \Rightarrow 2.\frac{{{{\left( {m + 1} \right)}^2}}}{9} = m \Leftrightarrow 2{m^2} + 4m + 2 = 9m \Leftrightarrow 2{m^2} - 5m + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\,\left( {tm} \right)\\m = \frac{1}{2}\,\,\,\left( {tm} \right)\end{array} \right.\)
Chọn C.
Câu hỏi 43 :
Tìm tất cả các số thực m để phương trình \(2{x^2} - 4x + 1 + {m^2} = 0\) có hai nghiệm phân biệt.
- A \( - 1 < m < 1\).
- B \( - 1 \le m < 1\).
- C \(0 \le m \le 1\).
- D \(0 \le m < 1\).
Đáp án: A
Phương pháp giải:
Phương trình \(a{x^2} + bx + c = 0\,\,\,\,(a \ne 0)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0\)
Lời giải chi tiết:
Phương trình \(2{x^2} - 4x + 1 + {m^2} = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)
\( \Leftrightarrow {2^2} - 2\left( {1 + {m^2}} \right) > 0 \Leftrightarrow 2{m^2} - 2 < 0 \Leftrightarrow {m^2} < 1 \Leftrightarrow - 1 < m < 1\)
Chọn A.
Câu hỏi 44 :
Giải phương trình \(\left| {3x + 1} \right| = x + 3\) ta được số nghiệm của phương trình là:
- A 1
- B 0
- C 2
- D 3
Đáp án: C
Phương pháp giải:
Giải phương trình chứa dấu giá trị tuyệt đối và đếm số nghiệm.
Lời giải chi tiết:
\(\left| {3x + 1} \right| = x + 3 \Leftrightarrow \left\{ \begin{array}{l}x + 3 \ge 0\\9{x^2} + 6x + 1 = {x^2} + 6x + 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\{x^2} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\\left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Vậy phương trình có 2 nghiệm.
Chọn C.
Câu hỏi 45 :
Tất cả giá trị của a để phương trình \(2x - 1 = 4 + 5a\) (với a là tham số) có nghiệm dương là
- A \(a = - 1\)
- B \(a > - 1\)
- C \(a = 0\)
- D \(a < - 1\)
Đáp án: B
Phương pháp giải:
Giải phương trình và biện luận.
Lời giải chi tiết:
\(2x - 1 = 4 + 5a \Leftrightarrow 2x = 5a + 5 \Leftrightarrow x = \frac{{5a + 5}}{2}\)
Để phương trình có nghiệm dương \( \Leftrightarrow \frac{{5a + 5}}{2} > 0 \Leftrightarrow 5a + 5 > 0 \Leftrightarrow a > - 1\)
Chọn B.
Câu hỏi 46 :
Cho phương trình \({x^2} - 4x + 1 = 0\) có 2 nghiệm \({x_1},{x_2}\).
Tính giá trị biểu thức \(P = {x_1} + {x_2} + {x_1}{x_2}\).
- A 3
- B 2
- C 4
- D 5
Đáp án: D
Phương pháp giải:
Áp dụng hệ thức Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right..\)
Lời giải chi tiết:
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}.{x_2} = 1\end{array} \right.\)
\(P = {x_1} + {x_2} + {x_1}{x_2} = 4 + 1 = 5\)
Chọn D.
Câu hỏi 47 :
Tập nghiệm của phương trình \(\left| {3x - 1} \right| = 2\) là
- A \(\left\{ { - \frac{1}{3};1} \right\}\)
- B \(\left\{ { - \frac{1}{3}} \right\}\)
- C \(\left\{ 1 \right\}\)
- D \(\left\{ {\frac{1}{3};1} \right\}\)
Đáp án: A
Phương pháp giải:
\(\left| {f\left( x \right)} \right| = a > 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\\f\left( x \right) = - a\end{array} \right.\)
Lời giải chi tiết:
\(\left| {3x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}3x - 1 = 2\\3x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{{ - 1}}{3}\end{array} \right.\)
Vậy phương trình có tập nghiệm: \(S = \left\{ { - \frac{1}{3};\;1} \right\}.\)
Chọn A.
Câu hỏi 48 :
Tập nghiệm của phương trình \(\left| {\left| {x - 1} \right| - 2} \right| = 4\) là S. Vậy S là
- A \(\left\{ { - 7} \right\}\)
- B \(\left\{ { - 5} \right\}\)
- C \(\left\{ { - 5;7} \right\}\)
- D \(\left\{ {5; - 7} \right\}\)
Đáp án: C
Phương pháp giải:
\(\left| {f\left( x \right)} \right| = a > 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\\f\left( x \right) = - a\end{array} \right.\)
Lời giải chi tiết:
\(\left| {\left| {x - 1} \right| - 2} \right| = 4 \Leftrightarrow \left[ \begin{array}{l}\left| {x - 1} \right| - 2 = 4\\\left| {x - 1} \right| - 2 = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left| {x - 1} \right| = 6\\\left| {x - 1} \right| = - 2\,\,(VN)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x - 1 = 6\\x - 1 = - 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 7\\x = - 5\end{array} \right.\)
Vậy phương trình có tập nghiệm: \(S = \left\{ {7; - 5} \right\}.\)
Chọn C.
Câu hỏi 49 :
Giải phương trình sau: \(\sqrt {2x + 1} - \sqrt {3x - 8} = 1\)
- A \(x = 4\)
- B \(x = 3\)
- C \(x = 2\)
- D \(x = 1\)
Đáp án: A
Phương pháp giải:
Bình phương hai vế không âm: \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\)
Lời giải chi tiết:
Giải phương trình sau: \(\sqrt {2x + 1} - \sqrt {3x - 8} = 1\)
Điều kiện: \(\left\{ \begin{array}{l}3x - 8 \ge 0\\2x + 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{8}{3}\\x \ge - \frac{1}{2}\end{array} \right. \Leftrightarrow x \ge \frac{8}{3}.\)
\(\begin{array}{l}Pt \Leftrightarrow \sqrt {2x + 1} = 1 + \sqrt {3x - 8} \Leftrightarrow 2x + 1 = 1 + 2\sqrt {3x - 8} + 3x - 8\\ \Leftrightarrow 2\sqrt {3x - 8} = 8 - x \Leftrightarrow \left\{ \begin{array}{l}8 - x \ge 0\\4\left( {3x - 8} \right) = 64 - 16x + {x^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 8\\{x^2} - 28x + 96 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 8\\\left[ \begin{array}{l}x = 4\\x = 24\end{array} \right.\end{array} \right. \Leftrightarrow x = 4\;\;\left( {tm} \right)\end{array}\)
Vậy phương trình có tập nghiệm: \(S = \left\{ 4 \right\}.\)
Chọn A.
Câu hỏi 50 :
Cho hai hàm số \(y = \left( {m + 1} \right){x^2} + 3{m^2}x + m\) và \(y = \left( {m + 1} \right){x^2} + 12x + 2\). Tìm tất cả các giá trị của m để đồ thị hai hàm số đã cho không cắt nhau.
- A \(m = 2\)
- B \(m = - 2\)
- C \(m = \pm 2\)
- D \(m = 1\)
Đáp án: B
Phương pháp giải:
+) Để hai đồ thị hàm số không cắt nhau thì phương trình hoành độ giao điểm của 2 đồ thị hàm số vô nghiệm.
+) Phương trình dạng \(ax + b = 0\) vô nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b \ne 0\end{array} \right.\).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm:
\(\begin{array}{l}\,\,\,\,\,\,\left( {m + 1} \right){x^2} + 3{m^2}x + m = \left( {m + 1} \right){x^2} + 12x + 2\\ \Leftrightarrow 3{m^2}x + m = 12x + 2 \Leftrightarrow \left( {3{m^2} - 12} \right)x = 2 - m\,\,\left( * \right)\end{array}\)
Để hai đồ thị hàm số đã cho không cắt nhau thì phương trình (*) vô nghiệm
\( \Leftrightarrow \left\{ \begin{array}{l}3{m^2} - 12 = 0\\2 - m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \pm 2\\m \ne 2\end{array} \right. \Leftrightarrow m = - 2\).
Chọn B.
Câu hỏi 51 :
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn \(\left[ { - 5;10} \right]\) để phương trình \(\left( {m + 1} \right)x = \left( {3{m^2} - 1} \right)x + m - 1\) có nghiệm duy nhất. Tổng các phần tử trong S bằng:
- A 15
- B 16
- C 39
- D 40
Đáp án: C
Phương pháp giải:
Phương trình dạng \(ax + b = 0\) có nghiệm duy nhất \( \Leftrightarrow a \ne 0\). Khi đó phương trình có nghiệm \(x = \dfrac{{ - b}}{a}\).
Lời giải chi tiết:
Ta có \(\left( {m + 1} \right)x = \left( {3{m^2} - 1} \right)x + m - 1 \Leftrightarrow \left( {3{m^2} - m - 2} \right)x = 1 - m\,\,\left( * \right)\)
Phương trình ban đầu có nghiệm duy nhất \( \Leftrightarrow \) phương trình (*) có nghiệm duy nhất \( \Leftrightarrow 3{m^2} - m - 2 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\m \ne \dfrac{{ - 2}}{3}\end{array} \right.\).
Kết hợp điều kiện đề bài ta có \(\left\{ \begin{array}{l}m \in Z\\m \in \left[ { - 5;10} \right]\backslash \left\{ 1 \right\}\end{array} \right. \Rightarrow S = \left\{ {m \in Z|m \in \left[ { - 5;10} \right]\backslash \left\{ 1 \right\}} \right\}\).
Vậy tổng các phần tử của S bằng \(\left( { - 5} \right) + \left( { - 4} \right) + ... + \left( { - 1} \right) + 0 + 2 + 3 + 4 + ... + 10 = 39\).
Chọn C.
Câu hỏi 52 :
Tìm tất cả các giá trị thực của tham số m để phương trình \(\left( {{m^2} + m} \right)x = m + 1\) có nghiệm duy nhất \(x = 1\).
- A \(m = - 1\)
- B \(m \ne 0\)
- C \(m \ne - 1\)
- D \(m = 1\)
Đáp án: D
Phương pháp giải:
Cách 1: Phương trình dạng \(ax + b = 0\) có nghiệm duy nhất \( \Leftrightarrow a \ne 0\). Khi đó phương trình có nghiệm \(x = \dfrac{{ - b}}{a}\).
Cách 2: Thay \(x = 1\) vào phương trình tìm m. Với giá trị m vừa tìm được, thử lại xem với giá trị đó phương trình có nghiệm duy nhất \(x = 1\) không và kết luận.
Lời giải chi tiết:
Cách 1: Để phương trình có nghiệm duy nhất \( \Leftrightarrow {m^2} + m \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 1\end{array} \right.\).
Khi đó phương trình có nghiệm duy nhất \(x = \dfrac{{m + 1}}{{{m^2} + m}} = \dfrac{{m + 1}}{{m\left( {m + 1} \right)}} = \dfrac{1}{m}\).
Do phương trình có nghiệm duy nhất \(x = 1 \Rightarrow \dfrac{1}{m} = 1 \Leftrightarrow m = 1\,\,\left( {tm} \right)\),
Vậy \(m = 1\).
Cách 2: Do \(x = 1\) là nghiệm của phương trình đã cho nên thay \(x = 1\) vào phương trình ta có:
\({m^2} + m = m + 1 \Leftrightarrow {m^2} = 1 \Leftrightarrow m = \pm 1\).
Thử lại:
+) Với \(m = 1\), phương trình trở thành \(2x = 2 \Leftrightarrow x = 1 \Rightarrow \) Phương trình có nghiệm duy nhất \(x = 1\). Vậy \(m = 1\) thỏa mãn.
+) Với \(m = - 1\), phương trình trở thành \(0x = 0 \Rightarrow \) Phương trình có vô số nghiệm \( \Rightarrow m = - 1\) không thỏa mãn.
Vậy \(m = 1\).
Chọn D.
Câu hỏi 53 :
Cho hai hàm số \(y = \left( {m + 1} \right)x + 1\) và \(y = \left( {3{m^2} - 1} \right)x + m\). Tìm tất cả các giá trị thực của tham số m để đồ thị hai hàm số đã cho trùng nhau.
- A \(m = 1,\,\,m = \dfrac{{ - 2}}{3}\)
- B \(m \ne 1\) và \(m \ne \dfrac{{ - 2}}{3}\)
- C \(m = 1\)
- D \(m = \dfrac{{ - 2}}{3}\)
Đáp án: C
Phương pháp giải:
+) Để hai đồ thị hàm số trùng nhau thì phương trình hoành độ giao điểm của 2 đồ thị hàm số có vô số nghiệm.
+) Phương trình dạng \(ax + b = 0\) có vô số nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\).
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm \(\left( {m + 1} \right)x + 1 = \left( {3{m^2} - 1} \right)x + m \Leftrightarrow \left( {3{m^2} - m - 2} \right)x = 1 - m\) (*)
Để hai đồ thị hàm số trùng nhau thì phương trình (*) có vô số nghiệm
\( \Leftrightarrow \left\{ \begin{array}{l}3{m^2} - m - 2 = 0\\1 - m = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m = \dfrac{{ - 2}}{3}\end{array} \right.\\m = 1\end{array} \right. \Leftrightarrow m = 1\).
Chọn C.
Câu hỏi 54 :
Cho phương trình \(\left( {{m^2} - 2m} \right)x = {m^2} - 3m + 2\). Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm?
- A \(m = 0\)
- B \(m = 2\)
- C \(m \ne 0,\,\,m \ne 2\)
- D \(m \ne 0\)
Đáp án: D
Phương pháp giải:
Phương trình dạng \(ax + b = 0\) có nghiệm khi và chỉ khi xảy ra 2 trường hợp:
+) Phương trình có nghiệm duy nhất \( \Leftrightarrow a \ne 0\).
+) Phương trình có vô số nghiệm \( \Leftrightarrow a = b = 0\).
Lời giải chi tiết:
TH1 : Phương trình đã cho có nghiệm duy nhất \( \Leftrightarrow {m^2} - 2m \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne 2\end{array} \right.\).
TH2 : Phương trình đã cho có vô số nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m = 0\\{m^2} - 3m + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\\\left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\end{array} \right. \Leftrightarrow m = 2\).
Kết hợp 2 trường hợp ta có phương trình có nghiệm \( \Leftrightarrow m \ne 0\).
Vậy có vô số giá trị của m thỏa mãn \( \Rightarrow m \ne 0\).
Chọn D.
Câu hỏi 55 :
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x + {m^2} + 4m + 5 = 0\). Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm đúng với mọi \(x \in R\)?
- A \(m = - 2\)
- B \(m = - 5\)
- C \(m = 1\)
- D Không tồn tại m
Đáp án: D
Phương pháp giải:
Phương trình dạng \(ax + b = 0\) có vô số nghiệm (nghiệm đúng với mọi \(x \in R\))\( \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\).
Lời giải chi tiết:
Phương trình đã cho có nghiệm đúng với mọi \(x \in R \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 2 = 0\\{m^2} + 4m + 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left\{ \begin{array}{l}m = 2\\m = 1\end{array} \right.\\Vo\,\,nghiem\end{array} \right. \Rightarrow \)Không tồn tại m thỏa mãn yêu cầu bài toán.
Chọn D.
Câu hỏi 56 :
Tìm tất cả các giá trị thực của tham số m để phương trình \(\left( {x - 1} \right)\left( {{x^2} - 4mx - 4} \right) = 0\) có ba nghiệm phân biệt.
- A \(m \in \mathbb{R}\)
- B \(m \ne 0\)
- C \(m \ne \dfrac{3}{4}\)
- D \(m \ne - \dfrac{3}{4}\)
Đáp án: D
Phương pháp giải:
+) \(\left( {x - 1} \right)\left( {{x^2} - 4mx - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\,\,\,\left( 1 \right)\\{x^2} - 4mx - 4 = 0\,\,\left( 2 \right)\end{array} \right.\)
+) Phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi phương trình (2) có 2 nghiệm phân biệt không trùng với phương trình (1).
Lời giải chi tiết:
Ta có : \(\left( {x - 1} \right)\left( {{x^2} - 4mx - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\{x^2} - 4mx - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\g\left( x \right) = {x^2} - 4mx - 4 = 0\end{array} \right.\)
Để phương trình ban đầu có 3 nghiệm phân biệt thì :
\(\left\{ \begin{array}{l}{\Delta _g}' = {\left( {2m} \right)^2} + 4 > 0\\g\left( 1 \right) \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{m^2} + 4 > 0\,\,\left( {luon\,\,dung} \right)\\1 - 4m - 4 \ne 0\end{array} \right. \Leftrightarrow m \ne - \dfrac{3}{4}\).
Chọn D.
Câu hỏi 57 :
Tìm tất cả các giá trị thực của tham số m để phương trình \(3{x^2} - \left( {m + 2} \right)x + m - 1 = 0\) có một nghiệm gấp đôi nghiệm còn lại.
- A \(m \in \left\{ {\dfrac{5}{2};7} \right\}\)
- B \(m \in \left\{ { - 2;\dfrac{{ - 1}}{2}} \right\}\)
- C \(m \in \left\{ {0;\dfrac{2}{5}} \right\}\)
- D \(m \in \left\{ {\dfrac{{ - 3}}{4};1} \right\}\)
Đáp án: A
Phương pháp giải:
+) Tìm điều kiện để phương trình có nghiệm.
+) Khi phương trình bậc hai \(a{x^2} + bx + c = 0\) có 2 nghiệm \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\).
Lời giải chi tiết:
Xét phương trình \(3{x^2} - \left( {m + 2} \right)x + m - 1 = 0\) ta có:
\(\Delta = {\left( {m + 2} \right)^2} - 12\left( {m - 1} \right) = {m^2} - 8m + 16 = {\left( {m - 4} \right)^2} \ge 0\,\,\forall m \Rightarrow \) Phương trình luôn có nghiệm với mọi giá trị của m.
Gọi \({x_1},\,\,{x_2}\) là 2 nghiệm của phương trình đã cho, áp dụng định lí Vi-ét ta có : \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{m + 2}}{3}\\{x_1}{x_2} = \dfrac{{m - 1}}{3}\end{array} \right.\,\,\left( * \right)\).
Theo bài ra, không mất tính tổng quát ta có : \({x_1} = 2{x_2}\), thay vào (*) ta có :
\(\begin{array}{l}\left\{ \begin{array}{l}2{x_2} + {x_2} = \dfrac{{m + 2}}{3}\\2x_2^2 = \dfrac{{m - 1}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = \dfrac{{m + 2}}{9}\\x_2^2 = \dfrac{{m - 1}}{6}\end{array} \right. \Leftrightarrow {\left( {\dfrac{{m + 2}}{9}} \right)^2} = \dfrac{{m - 1}}{6}\\ \Leftrightarrow \dfrac{{{{\left( {m + 2} \right)}^2}}}{{27}} = \dfrac{{m - 1}}{2} \Leftrightarrow 2{m^2} + 8m + 8 = 27m - 27 \Leftrightarrow 2{m^2} - 19m + 35 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 7\\m = \dfrac{5}{2}\end{array} \right.\end{array}\)
Chọn A.
Câu hỏi 58 :
Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\) (m là tham số). Tìm m để biểu thức \(P = {x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) - 6\) đạt giá trị nhỏ nhất.
- A \(m = \dfrac{1}{2}\)
- B \(m = 1\)
- C \(m = 2\)
- D \(m = - 12\)
Đáp án: C
Phương pháp giải:
+) Khi phương trình bậc hai \(a{x^2} + bx + c = 0\) có 2 nghiệm \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\).
+) Đưa biểu thức \(P\) về dạng \(P = {f^2}\left( m \right) + A\) (\(A\) là hằng số) và đánh giá.
Lời giải chi tiết:
Phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = {\left( {m + 1} \right)^2} - {m^2} - 2 = 2m - 1 > 0 \Leftrightarrow m > \dfrac{1}{2}\).
Giả sử phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\) có hai nghiệm là \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 2\\{x_1}{x_2} = {m^2} + 2\end{array} \right.\).
Khi đó
\(\begin{array}{l}P = {x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) - 6 = {m^2} + 2 - 2\left( {2m + 2} \right) - 6\\P = {m^2} - 4m - 8 = {m^2} - 4m + 4 - 12 = {\left( {m - 2} \right)^2} - 12 \ge - 12\end{array}\)
\( \Rightarrow {P_{\min }} = - 12\). Dấu "=" xảy ra \( \Leftrightarrow m = 2\).
Chọn C.
Câu hỏi 59 :
Với giá trị nào của \(m\) thì phương trình \(m{x^2} - 2\left( {m - 2} \right)x + 3 - m = 0\) có hai nghiệm trái dấu?
- A \(0 < m < 3\)
- B \(m < 0\)
- C \(m < 0\) hoặc \(m > 3\)
- D \(m > 3\)
Đáp án: C
Phương pháp giải:
Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm trái dấu \( \Leftrightarrow ac < 0.\)
Lời giải chi tiết:
Phương trình \(m{x^2} - 2\left( {m - 2} \right)x + 3 - m = 0\) có hai nghiệm trái dấu
\( \Leftrightarrow m\left( {3 - m} \right) < 0 \Leftrightarrow m\left( {m - 3} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}m > 3\\m < 0\end{array} \right..\)
Chọn C.
Câu hỏi 60 :
Cho \(f\left( x \right) = m\left( {m + 2} \right){x^2} - 2mx + 2\). Tìm m để \(f\left( x \right) = 0\) có hai nghiệm dương phân biệt.
- A \(m \in \left( { - 4;0} \right)\)
- B \(m \in \emptyset \)
- C \(m \in \left( { - 4; - 2} \right)\)
- D \(m \in \left( { - 2;0} \right)\)
Đáp án: B
Phương pháp giải:
Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta > 0\\S > 0\\P > 0\end{array} \right..\)
Lời giải chi tiết:
Phương trình \(m\left( {m + 2} \right){x^2} - 2mx + 2 = 0\) có hai nghiệm dương phân biệt
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m\left( {m + 2} \right) \ne 0\\\Delta ' = {m^2} - 2m\left( {m + 2} \right) > 0\\S = \frac{{2m}}{{m\left( {m + 2} \right)}} > 0\\P = \frac{2}{{m\left( {m + 2} \right)}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\ - {m^2} - 4m > 0\\\frac{{2m}}{{m\left( {m + 2} \right)}} > 0\\m\left( {m + 2} \right) > 0\;\;\left( {do\;2 > 0} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\m\left( {m + 4} \right) < 0\\m > 0\\m + 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\ - 4 < m < 0\\m > - 2\\m > 0\end{array} \right. \Rightarrow m \in \emptyset .\end{array}\)
Vậy \(m \in \emptyset .\)
Chọn B.
Tổng hợp các bài tập trắc nghiệm phương trình mức độ vận dụng, vận dụng cao có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm phương trình mức độ thông hiểu có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm phương trình mức độ nhận biết có đáp án và lời giải chi tiết
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục