Phương pháp giải:

Áp dụng lý thuyết phương trình chính tắc của elip.

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\) với \(a > b > 0\) và \({a^2} = {b^2} + {c^2}\) với \(2c\) là tiêu cự của (E).

Lời giải chi tiết:

Theo lý thuyết phương trình chính tắc của elip có \({a^2} = {b^2} + {c^2}\)

Đáp án: C 

Phương pháp giải:

Tính tỉ số \(e = {c \over a}\) trong đó

Lời giải chi tiết:

Elip có độ dài trục bé bằng tiêu cự nên ta có \(b = c\). Mặt khác ta có \({a^2} = {b^2} + {c^2}\), suy ra \({a^2} = 2{c^2}\) hay \(a = \sqrt 2 c\).

Tâm sai của elip là: \(e = {c \over a} = {c \over {\sqrt 2 c}} = {1 \over {\sqrt 2 }}\).

Đáp án: A

Phương pháp giải:

Từ phương trình của elip và lý thuyết elip tìm các hệ số \(a,b,c\) rồi kết luận.

Lời giải chi tiết:

Từ phương trình elip \((E):{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\) ta có \(\left\{ \matrix{  a = 5 \hfill \cr   b = 3 \hfill \cr   c = \sqrt {{a^2} - {b^2}}  = 4 \hfill \cr}  \right.\)

Suy ra ta có:

       I.            \((E)\) có các tiêu điểm \({F_1}( - 4;0)\) và \({F_2}(4;0)\)

    II.            \((E)\) có tỉ số \({c \over a} = {4 \over 5}\)

 III.            \((E)\) có đỉnh \({A_1}( - 5;0)\)

 IV.            \((E)\) có độ dài trục nhỏ bằng \(2b = 6\).

Đáp án: D

Phương pháp giải:

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\)

Lời giải chi tiết:

Độ dài trục lớn là 12, suy ra \(2a = 12\) hay \(a = 6\)

Độ dài trục nhỏ là 8, suy ra \(2b = 8\) hay \(b = 4\)

Vậy elip cần tìm là \({{{x^2}} \over {36}} + {{{y^2}} \over {16}} = 1\)

Đáp án: A

Phương pháp giải:

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\)

Chú ý Elip có 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right)\)

Lời giải chi tiết:

Elip có  hai đỉnh là \(A(5;0)\) và \(B(0;3)\) suy ra \(a = 5\) và \(b = 3\). Do đó, phương trình chính tắc của elip là: \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\)

Đáp án: C 

Phương pháp giải:

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\).

Lời giải chi tiết:

Elip có tiêu điểm \({F_1}(4;0)\) suy ra \(c = 4\), elip có một đỉnh là  \(A(5;0)\) suy ra \(a = 5\).

Mặt khác ta có \({b^2} = {a^2} - {c^2} = 25 - 16 = 9\).

Vậy elip có phương trình là \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\).

Đáp án: C

Phương pháp giải:

- Quan sát đồ thị, dễ dàng nhận thấy rằng OM lớn nhất khi M trùng với điểm \((6;\,0)\) hoặc \(( - 6;0)\).

- Sử dụng phương pháp thế và đánh giá để chứng minh nhận xét trên.

Lời giải chi tiết:

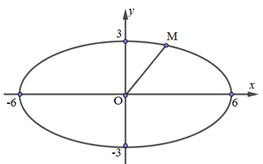
\(M \in (E) \Rightarrow M({x_0};{y_0}):\,\,\,\,{{{x_0}^2} \over {36}} + {{{y_0}^2} \over 9} = 1 \Leftrightarrow {x_0}^2 = 36 - 4{y_0}^2\)

Ta có: \(O{M^2} = {x_0}^2 + {y_0}^2 = 36 - 4{y_0}^2 + {y_0}^2 = 36 - 3{y_0}^2 \le 36\)

\( \Rightarrow OM \le 6\,\,\,\,\,\,\, \Rightarrow O{M_{\max }} = 6\) khi và chỉ khi \({y_0} = 0 \Leftrightarrow {x_0} =  \pm 6\)

Chọn: B

Phương pháp giải:

- Quan sát đồ thị, dễ dàng nhận thấy rằng OM nhỏ nhất khi M trùng với điểm \((0;\,3)\) hoặc \((0; - 3)\).

- Sử dụng phương pháp thế và đánh giá để chứng minh nhận xét trên.

Lời giải chi tiết:

\(M \in (E) \Rightarrow M({x_0};{y_0}):\,\,\,\,9{x_0}^2 + 16{y_0}^2 = 144 \Leftrightarrow {y_0}^2 = 9 - {9 \over {16}}{x_0}^2\)

Ta có: \(O{M^2} = {x_0}^2 + {y_0}^2 = {x_0}^2 + 9 - {9 \over {16}}{x_0}^2 = {7 \over {16}}{x_0}^2 + 9 \ge 9\)

\( \Rightarrow OM \ge 3\,\,\,\,\,\, \Rightarrow O{M_{\min }} = 3\) khi và chỉ khi \({x_0} = 0 \Leftrightarrow {y_0} =  \pm 3\)

Chọn: B

Phương pháp giải:

Đưa phương trình Elip về đúng dạng, xác định các hệ số a, b, c.

Viết phương trình đường thẳng D.

Giải hệ phương trình để tìm giao điểm của D và (E).

Lời giải chi tiết:

Ta có: \((E):\,\,9{x^2} + 25{y^2} = 225 \Leftrightarrow {{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1 \Rightarrow a = 5,\,\,b = 3\)

Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {5^2} - {3^2} = 16 \Rightarrow c = 4 \Rightarrow \,\,{F_1}( - 4;0)\).

Phương trình đường thẳng D qua tiêu điểm \({F_1}\), vuông góc \(Ox\): \(x =  - 4\).

Tọa độ điểm M, N là nghiệm của hệ phương trình: \(\left\{ \matrix{  9{x^2} + 25{y^2} = 225 \hfill \cr   x =  - 4 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  x =  - 4 \hfill \cr   9.{( - 4)^2} + 25.{y^2} = 225 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  x =  - 4 \hfill \cr   y =  \pm {9 \over 5} \hfill \cr}  \right.\)

\( \Rightarrow M\left( { - {9 \over 5}; - 4} \right),\,\,N\left( {{9 \over 5}; - 4} \right) \Rightarrow MN = {{18} \over 5}\)

Chọn: D

Phương pháp giải:

Xác định các hệ số a, b, c.

Sử dụng công thức \(M{F_1} = a + {c \over a}{x_0}\)

Lời giải chi tiết:

\((E):\,\,{{{x^2}} \over {25}} + {{{y^2}} \over {16}} = 1 \Rightarrow a = 5,\,\,b = 4\)

Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {5^2} - {4^2} = 9 \Rightarrow c = 3\)

Gọi \(M\left( {{x_0};{y_0}} \right) \in (E) \Rightarrow {{{x_0}^2} \over {25}} + {{{y_0}^2} \over {16}} = 1\)

\(M{F_1} = a + {c \over a}{x_0} = 5 + {3 \over 5}{x_0} = 3 \Rightarrow {x_0} =  - {{10} \over 3}\)

Ta có:  \({{{x_0}^2} \over {25}} + {{{y_0}^2} \over {16}} = 1 \Leftrightarrow {{{{\left( { - {{10} \over 3}} \right)}^2}} \over {25}} + {{{y_0}^2} \over {16}} = 1 \Leftrightarrow {y_0}^2 = {{80} \over 9} \Leftrightarrow {y_0} =  \pm {{4\sqrt 5 } \over 3}\)

Vậy, \(M\left( { - {{10} \over 3}; - {{4\sqrt 5 } \over 3}} \right)\) hoặc \(M\left( { - {{10} \over 3};{{4\sqrt 5 } \over 3}} \right)\).

Chọn: C

Phương pháp giải:

Xác định các hệ số a, b, c.

\(M{F_1} + M{F_2} = 2a,\,\,\,M{F_1} = a + {c \over a}{x_0},\,\,\,M{F_2} = a - {c \over a}{x_0}\)

Lời giải chi tiết:

\((E):\,\,{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1 \Rightarrow a = 5,\,\,b = 3\)

Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {5^2} - {3^2} = 16 \Rightarrow c = 4\).

Gọi \(M\left( {{x_0};{y_0}} \right) \in (E) \Rightarrow \,{{{x_0}^2} \over {25}} + {{{y_0}^2} \over 9} = 1\)

\(M{F_1} + M{F_2} = 2.5 = 10\)

Theo đề bài, ta có: \(M{F_1} - M{F_2} = 2 \Rightarrow \left\{ \matrix{  M{F_1} = {{10 + 2} \over 2} = 6 \hfill \cr   M{F_2} = {{10 - 2} \over 2} = 4 \hfill \cr}  \right.\)

\(M{F_1} = a + {c \over a}{x_0} = 5 + {4 \over 5}{x_0} = 6 \Rightarrow {x_0} = {5 \over 4}\)

Mà \(\,{{{x_0}^2} \over {25}} + {{{y_0}^2} \over 9} = 1 \Rightarrow {{{{\left( {{5 \over 4}} \right)}^2}} \over {25}} + {{{y_0}^2} \over 9} = 1 \Leftrightarrow {y_0} =  \pm {{3\sqrt {15} } \over 4}\)

Vậy \(M\left( {{5 \over 4}; - {{3\sqrt {15} } \over 4}} \right)\) hoặc \(M\left( {{5 \over 4};{{3\sqrt {15} } \over 4}} \right)\).

Chọn: D

Phương pháp giải:

Xác định các hệ số a, b, c.

Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc góc phần tư thứ (III) \( \Leftrightarrow \left\{ \matrix{  {x_0} < 0 \hfill \cr   {y_0} < 0 \hfill \cr}  \right.\)

Bán kính qua tiêu bằng \({5 \over 2} \Leftrightarrow \left[ \matrix{  M{F_1} = {5 \over 2} \hfill \cr   M{F_2} = {5 \over 2} \hfill \cr}  \right.\)

Sử dụng các công thức \(M{F_1} = a + {c \over a}{x_0};\,\,M{F_2} = a - {c \over a}{x_0}\)

Lời giải chi tiết:

\((E):\,\,{{{x^2}} \over {16}} + {{{y^2}} \over 7} = 1 \Rightarrow a = 4,\,\,b = \sqrt 7 \)

Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {4^2} - {\left( {\sqrt 7 } \right)^2} = 9 \Rightarrow c = 3\).

Gọi \(M\left( {{x_0};{y_0}} \right) \in (E) \Rightarrow {{{x_0}^2} \over {16}} + {{{y_0}^2} \over 7} = 1\)

\(M\) nằm trong góc phần tư thứ (III) \( \Leftrightarrow {x_0} < 0,\,\,\,\,{y_0} < 0\)

Theo đề bài, ta có: \(\left[ \matrix{  M{F_1} = {5 \over 2} \Leftrightarrow a + {c \over a}{x_0} = {5 \over 2} \Leftrightarrow 4 + {3 \over 4}{x_0} = {5 \over 2} \Leftrightarrow {x_0} =  - 2\,\,\left( {tm} \right) \hfill \cr   M{F_2} = {5 \over 2} \Leftrightarrow a - {c \over a}{x_0} = {5 \over 2} \Leftrightarrow 4 - {3 \over 4}{x_0} = {5 \over 2} \Leftrightarrow {x_0} = 2\,\,\left( {ktm} \right) \hfill \cr}  \right.\)

Mà  \({{{x_0}^2} \over {16}} + {{{y_0}^2} \over 7} = 1 \Rightarrow {{{{( - 2)}^2}} \over {16}} + {{{y_0}^2} \over 7} = 1 \Leftrightarrow \left[ \matrix{  {y_0} = {{\sqrt {21} } \over 2}\,\,\,\,\,\,\,\,\left( {ktm} \right) \hfill \cr   {y_0} =  - {{\sqrt {21} } \over 2}\,\,\,\,\left( {tm} \right) \hfill \cr}  \right.\)

Vậy, \(M\left( { - 2; - {{\sqrt {21} } \over 2}} \right)\)

Chọn: A

Phương pháp giải:

\((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)

Sử dụng công thức \({a^2} - {b^2} = {c^2}\) tính c. Từ đó, kết luận tiêu điểm của (E) là \({F_1}( - c;0),\,\,{F_2}(c;0)\).

Lời giải chi tiết:

\((E):\,\,\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1 \Rightarrow a = 10,\,\,b = 6\)

Mà \({a^2} - {b^2} = {c^2} \Leftrightarrow {c^2} = {10^2} - {6^2} = 64 \Rightarrow c = 8 \Rightarrow {F_1}( - 8;0),\,\,{F_2}(8;0)\)

Chọn: D

Phương pháp giải:

\((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)

Sử dụng công thức \({a^2} - {b^2} = {c^2}\) tính tiêu cự c.

Tính tâm sai \(e = \frac{c}{a}\).

Lời giải chi tiết:

\((E):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1 \Rightarrow a = 5,\,\,b = 4\)

Mà \({a^2} - {b^2} = {c^2} \Leftrightarrow {c^2} = {5^2} - {4^2} = 9 \Rightarrow c = 3\)

Tâm sai \(e = \frac{c}{a} = \frac{3}{5}\)

Chọn: C

Phương pháp giải:

Tiêu cự của elip có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) là \(2c = 2\sqrt {{a^2} - {b^2}} .\)

Lời giải chi tiết:

Tiêu cự của \(\left( E \right)\) là \(2\sqrt {25 - 9}  = 2.\sqrt {16}  = 2.4 = 8\)

Chọn A.

Phương pháp giải:

Phương trình chính tắc của Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \({a^2} - {b^2} = {c^2}\,\,(a > b)\)

Lời giải chi tiết:

Phương trình \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\) là phương trình chính tắc của 1 Elip

Chọn D.

Lời giải chi tiết:

Ta có: \(a = 5,\,\,b = 4 \Rightarrow {c^2} = {a^2} - {b^2} = 9 \Rightarrow c = 3\).

\( \Rightarrow e = \dfrac{c}{a} = \dfrac{3}{5}\).

Chọn B.

Lời giải chi tiết:

\(*\,\,a = 4,\,\,b = 3 \Rightarrow {c^2} = {a^2} - {b^2} = 7 \Rightarrow c = \sqrt 7 \).

* Ta có \({F_2}\left( {c;0} \right) \Rightarrow {F_2}\left( {\sqrt 7 ;0} \right)\).

Chọn C.

Phương pháp giải:

Tiêu cự của elip có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) là \(2c = 2\sqrt {{a^2} - {b^2}} .\)

Lời giải chi tiết:

Đường Elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\) có tiêu cự bằng \(2\sqrt {16 - 7}  = 2\sqrt 9  = 6\)

Chọn A.

Phương pháp giải:

Với \({F_1}\left( { - c;\,\,0} \right),\,\,{F_2}\left( {c;\,\,0} \right)\) ta có: \(M\left( {x;y} \right) \in \left( E \right) \Leftrightarrow \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\,\,\left( 1 \right)\) trong đó \({b^2} = {a^2} - {c^2}\)

Phương trình \(\left( 1 \right)\) được gọi là phương trình chính tắc của elip \(\left( E \right)\).

Lời giải chi tiết:

Phương trình \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{16}} = 1\) được viết dưới dạng \(\frac{{{x^2}}}{{{3^3}}} + \frac{{{y^2}}}{{{4^2}}} = 1\) (là dạng phương trình chính tắc của Elip)

Phương trình chính tắc của Elip là: \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{16}} = 1\)

Chọn  C.

Phương pháp giải:

Elip \(\left( E \right):\,\,\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow {c^2} = {a^2} - {b^2}\)

\( \Rightarrow \)Tiêu điểm của elip là \({F_1}\left( {c;\,\,0} \right),\,\,{F_2}\left( { - c;\,\,0} \right)\).

Lời giải chi tiết:

Xét Elip \(\left( E \right):\,\,\,\frac{{{x^2}}}{9} + \frac{{{y^2}}}{6} = 1\) ta có:

\(\left\{ \begin{array}{l}{a^2} = 9\\{b^2} = 6\end{array} \right. \Rightarrow {c^2} = {a^2} - {b^2} = 9 - 6 = 3 \Rightarrow c = \sqrt 3 \)

\( \Rightarrow \) Elip \(\left( E \right)\) có hai tiêu điểm là \({F_1}\left( { - \sqrt 3 ;\,\,0} \right)\) và \({F_2}\left( {\sqrt 3 ;\,\,0} \right)\).

Chọn  D.

Phương pháp giải:

Phương trình chính tắc của Elip \(\left( E \right)\) là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), có độ dài trục lớn là \({A_1}{A_2} = 2a\).

Lời giải chi tiết:

Xét Elip \(\left( E \right):\,\,\,\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) ta có:  \(\left\{ \begin{array}{l}{a^2} = 25\\{b^2} = 9\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 5\\b = 3\end{array} \right.\)

Độ dài trục lớn là: \({A_1}{A_2} = 2.\,5 = 10\)

Vậy độ dài trục lớn của Elip \(\left( E \right)\) là \(10.\)

Chọn B.

Phương pháp giải:

\(\left( E \right):\,\,\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có tâm sai \(e = \frac{c}{a}\).

Lời giải chi tiết:

Xét Elip \(\left( E \right):\,\,\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) ta có:

\(\left\{ \begin{array}{l}{a^2} = 25\\{b^2} = 9\end{array} \right. \Rightarrow {c^2} = {a^2} - {b^2} = 25 - 9 = 16\)\( \Rightarrow c = 4\) (Do \(c > 0\))

Vậy tâm sai của elip \(\left( E \right)\) là \(e = \frac{c}{a} = \frac{4}{5} \cdot \)

Chọn  A.

Phương pháp giải:

Elip \(\left( E \right):\,\,\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow {c^2} = {a^2} - {b^2}\)

\( \Rightarrow \)Tiêu điểm của elip là \({F_1}\left( {c;\,\,0} \right),\,\,{F_2}\left( { - c;\,\,0} \right).\)

Lời giải chi tiết:

Xét elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 6,\) ta có: \(\left\{ \begin{array}{l}{a^2} = 16\\{b^2} = 9\end{array} \right. \Rightarrow {c^2} = {a^2} - {b^2} \Rightarrow c = \sqrt {{a^2} - {b^2}}  = \sqrt 7 \)

Vậy elip có hai tiêu điểm là \({F_1}\left( { - \sqrt 7 ;\,\,0} \right),\,\,{F_2}\left( {\sqrt 7 ;\,\,0} \right).\)

Chọn A.

Phương pháp giải:

Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có tiêu cự \(2c\) với \(c = \sqrt {{a^2} - {b^2}} \).

Lời giải chi tiết:

\(\begin{array}{l}\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\\ \Rightarrow {a^2} = 25,\,\,\,{b^2} = 9\\ \Rightarrow {c^2} = {a^2} - {b^2} = 25 - 9 = 16\\ \Rightarrow c = 4\end{array}\)

Vậy tiêu cự là \(2c = 2.4 = 8\).

Chọn B.