Phương pháp giải:

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\).

Lời giải chi tiết:

Elip có  hai tiêu điểm là \({F_1}( - 1;0),{F_2}(1;0)\) suy ra \(c = 1\)

 Elip có tâm sai \(e = {1 \over 5}\) suy ra \({c \over a} = {1 \over 5} \Rightarrow a = 5\)

Mặt khác ta có \({b^2} = {a^2} - {c^2} = 25 - 1 = 24\)

Vậy elip có phương trình là \({{{x^2}} \over {25}} + {{{y^2}} \over {24}} = 1\)

Đáp án: C

Phương pháp giải:

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\).

Lời giải chi tiết:

Elip có một đỉnh là \(B(0; - 2)\) suy ra \(b = 2\).

Elip có tiêu cự là  \(2\sqrt 5 \) suy ra \(c = 2\sqrt 5  \Leftrightarrow c = \sqrt 5 \).

Mặt khác ta có \({a^2} = {b^2} + {c^2} = 4 + 5 = 9\).

Vậy elip có dạng \({{{x^2}} \over 9} + {{{y^2}} \over 4} = 1\).

Đáp án: D

Phương pháp giải:

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\)

Lời giải chi tiết:

Elip có một đỉnh là \(A(0; - 4)\) suy ra \(b = 4\).

Tâm sai  \(e = {3 \over 5}\) suy ra ta có \({c \over a} = {3 \over 5}\). Vì \(a,c > 0\) nên ta có  \({{{c^2}} \over {{a^2}}} = {9 \over {25}} \Leftrightarrow 25{c^2} - 9{a^2} = 0\)

Mặt khác ta có \({a^2} - {c^2} = {b^2} = 16\).

Ta có hệ phương trình \(\left\{ \matrix{  9{a^2} - 25{c^2} = 0 \hfill \cr   {a^2} - {c^2} = 16 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {a^2} = 25 \hfill \cr   {c^2} = 9 \hfill \cr}  \right.\).

Vậy phương trình của elip là: \({{{x^2}} \over {25}} + {{{y^2}} \over {16}} = 1\)

Đáp án: C

Phương pháp giải:

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\).

Lời giải chi tiết:

Elip có đỉnh là \(A(2;0)\) suy ra \(a = 2\). Phương trình elip cần tìm có dạng  \({{{x^2}} \over 4} + {{{y^2}} \over {{b^2}}} = 1\)

Vì elip qua \(M( - 1;{{\sqrt 3 } \over 2})\) nên ta có \({1 \over 4} + {3 \over {4{b^2}}} = 1 \Leftrightarrow {b^2} = 1\)

Vậy elip có phương trình là \({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\)

Đáp án: A

Phương pháp giải:

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\).

Chú ý: Elip đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) tức là ta có \({{x_0^2} \over {{a^2}}} + {{y_0^2} \over {{b^2}}} = 1\)

Lời giải chi tiết:

Phương trình elip cần tìm có dạng  \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)

Vì elip qua \(M\left( {2\sqrt 2 ;{1 \over 3}} \right)\) nên ta có \({8 \over {{a^2}}} + {1 \over {9{b^2}}} = 1\)

Vì elip qua \(N\left( {2;{{\sqrt 5 } \over 3}} \right)\) nên ta có \({4 \over {{a^2}}} + {5 \over {9{b^2}}} = 1\)

Ta có hệ phương trình \(\left\{ \matrix{  {8 \over {{a^2}}} + {1 \over {9{b^2}}} = 1 \hfill \cr   {4 \over {{a^2}}} + {5 \over {9{b^2}}} = 1 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {a^2} = 9 \hfill \cr   {b^2} = 1 \hfill \cr}  \right.\)

Vậy elip có phương trình là \({{{x^2}} \over 9} + {{{y^2}} \over 1} = 1\)

Đáp án: C

Phương pháp giải:

Đưa phương trình elip về dạng chính tắc.

Xác định các hệ số a, b, c.

Sử dụng các công thức \(M{F_1} = a + {c \over a}{x_0},\,\,M{F_2} = a - {c \over a}{x_0},\,\,{F_1}{F_2} = 2c\)

Áp dụng định lí Cosin trong tam giác \(M{F_1}{F_2}\)

Lời giải chi tiết:

Gọi \(M({x_0};{y_0}) \in (E) \Rightarrow \,16{x_0}^2 + 25{y_0}^2 = 400\).

\((E):\,\,16{x^2} + 25{y^2} = 400 \Leftrightarrow {{{x^2}} \over {25}} + {{{y^2}} \over {16}} = 1 \Rightarrow a = 5,b = 4\)

Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {5^2} - {4^2} = 9 \Rightarrow c = 3\)

\({F_1}{F_2} = 2c = 6\)

\(M{F_1} = a + {c \over a}{x_0} = 5 + {3 \over 5}{x_0};\,\,\,\,M{F_2} = a - {c \over a}{x_0}\, = 5 - {3 \over 5}{x_0}\)

Điểm \(M \in (E)\) nhìn 2 tiêu điểm dưới một góc \({60^0}\( \( \Rightarrow \widehat {{F_1}M{F_2}} = {60^0}\)

Áp dụng định lý Côsin, ta có: \({F_1}{F_2}^{2\;} = {\rm{ }}M{F_1}^2 + {\rm{ }}M{F_2}^2 - {\rm{ }}2M{F_1}.M{F_2}\cos {60^0}\)

\(\eqalign{  &  \Leftrightarrow {6^2} = {\left( {5 + {3 \over 5}{x_0}} \right)^2} + {\left( {5 - {3 \over 5}{x_0}} \right)^2} - 2\left( {5 + {3 \over 5}{x_0}} \right)\left( {5 - {3 \over 5}{x_0}} \right)\cos {60^0}  \cr   &  \Leftrightarrow 36 = {\left( {5 + {3 \over 5}{x_0}} \right)^2} + {\left( {5 - {3 \over 5}{x_0}} \right)^2} - 2\left( {5 + {3 \over 5}{x_0}} \right)\left( {5 - {3 \over 5}{x_0}} \right).{1 \over 2}  \cr   &  \Leftrightarrow 36 = 25 + 6{x_0} + {{9{x_0}^2} \over {25}} + 25 - 6{x_0} + {{9{x_0}^2} \over {25}} - 25 + {{9{x_0}^2} \over {25}}  \cr   &  \Leftrightarrow {{27{x_0}^2} \over {25}} = 11 \Leftrightarrow {x_0}^2 = {{275} \over {27}} \Leftrightarrow {x_0} =  \pm \sqrt {{{275} \over {27}}}  \cr} \)

 Ta có: \(16{x_0}^2 + 25{y_0}^2 = 400 \Leftrightarrow 16.{{275} \over {27}} + 25{y_0}^2 = 400 \Leftrightarrow {y_0}^2 = {{256} \over {27}} \Leftrightarrow {y_0} =  \pm \sqrt {{{256} \over {27}}} \)

Vậy, các điểm M thoả mãn yêu cầu đề bài là:

\({M_1}\left( {\sqrt {{{275} \over {27}}} ;\sqrt {{{256} \over {27}}} } \right);\,\,{M_2}\left( {\sqrt {{{275} \over {27}}} ; - \sqrt {{{256} \over {27}}} } \right);\,\,{M_3}\left( { - \sqrt {{{275} \over {27}}} ; - \sqrt {{{256} \over {27}}} } \right);\,\,{M_4}\left( { - \sqrt {{{275} \over {27}}} ;\sqrt {{{256} \over {27}}} } \right)\)

Chọn: A

Phương pháp giải:

Xác định các hệ số a, b, c.

Sử dụng các công thức \(M{F_1} = a + {c \over a}{x_0},\,\,M{F_2} = a - {c \over a}{x_0},\,\,{F_1}{F_2} = 2c\)

Áp dụng định lí Cosin trong tam giác \(M{F_1}{F_2}\)

Lời giải chi tiết:

Gọi \(M({x_0};{y_0}) \in (E) \Rightarrow \,{{{x_0}^2} \over {25}} + {{{y_0}^2} \over 4} = 1\).

\((E):\,\,{{{x^2}} \over {25}} + {{{y^2}} \over 4} = 1 \Rightarrow a = 5,\,b = 2\)

Mà \({a^2} - {b^2} = {c^2} \Rightarrow {c^2} = {5^2} - {2^2} = 21 \Rightarrow c = \sqrt {21} \)

\({F_1}{F_2} = 2c = 2\sqrt {21} \)

\(M{F_1} = a + {c \over a}{x_0} = 5 + {{\sqrt {21} } \over 5}{x_0};\,\,\,\,M{F_2} = a - {c \over a}{x_0}\, = 5 - {{\sqrt {21} } \over 5}{x_0}\)

Điểm \(M \in (E)\) nhìn 2 tiêu điểm dưới một góc \({120^0} \Rightarrow \widehat {{F_1}M{F_2}} = {120^0}\)

Áp dụng định lý Côsin, ta có: \({F_1}{F_2}^{2\;} = {\rm{ }}M{F_1}^2 + {\rm{ }}M{F_2}^2 - {\rm{ }}2M{F_1}.M{F_2}\cos {120^0}\)

\(\eqalign{  &  \Leftrightarrow {\left( {2\sqrt {21} } \right)^2} = {\left( {5 + {{\sqrt {21} } \over 5}{x_0}} \right)^2} + {\left( {5 - {{\sqrt {21} } \over 5}{x_0}} \right)^2} - 2\left( {5 + {{\sqrt {21} } \over 5}{x_0}} \right)\left( {5 - {{\sqrt {21} } \over 5}{x_0}} \right)\cos {120^0}  \cr   &  \Leftrightarrow 84 = {\left( {5 + {{\sqrt {21} } \over 5}{x_0}} \right)^2} + {\left( {5 - {{\sqrt {21} } \over 5}{x_0}} \right)^2} - 2\left( {5 + {{\sqrt {21} } \over 5}{x_0}} \right)\left( {5 - {{\sqrt {21} } \over 5}{x_0}} \right).{{ - 1} \over 2}  \cr   &  \Leftrightarrow 84 = 25 + 2\sqrt {21} {x_0} + {{21{x_0}^2} \over {25}} + 25 - 2\sqrt {21} {x_0} + {{21{x_0}^2} \over {25}} + 25 - {{21{x_0}^2} \over {25}}  \cr   &  \Leftrightarrow {{21{x_0}^2} \over {25}} = 9 \Leftrightarrow {x_0}^2 = {{75} \over 7} \Leftrightarrow {x_0} =  \pm \sqrt {{{75} \over 7}}  \cr} \)

 Ta có: \({{{x_0}^2} \over {25}} + {{{y_0}^2} \over 4} = 1 \Rightarrow {{{{75} \over 7}} \over {25}} + {{{y_0}^2} \over 4} = 1 \Leftrightarrow {y_0}^2 = {{16} \over 7} \Leftrightarrow {y_0} =  \pm {4 \over {\sqrt 7 }}\)

Vậy, có 4 điểm M thoả mãn yêu cầu đề bài là:

\({M_1}\left( {\sqrt {{{75} \over 7}} ;{4 \over {\sqrt 7 }}} \right);\,\,{M_2}\left( {\sqrt {{{75} \over 7}} ; - {4 \over {\sqrt 7 }}} \right);\,\,{M_3}\left( { - \sqrt {{{75} \over 7}} ;{4 \over {\sqrt 7 }}} \right);\,\,{M_4}\left( { - \sqrt {{{75} \over 7}} ; - {4 \over {\sqrt 7 }}} \right)\)

Chọn: D.

Phương pháp giải:

Lấy \(A\left( {{x_0};{y_0}} \right) \in \left( E \right)\), xác định điểm B đối xứng với A qua Ox.

Tam giác ABC đều \( \Leftrightarrow AB = AC\), giải phương trình tìm \({x_0};{y_0}\).

Lời giải chi tiết:

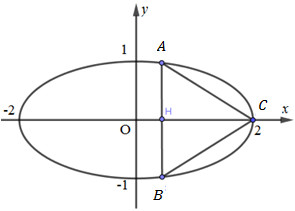
Giả sử \(A\left( {{x_0};{y_0}} \right)\). Do A, B đối xứng nhau qua Ox nên \(B({x_0}; - {y_0})\).

Ta có: \(A{B^2} = 4{y_0}^2,\,\,\,A{C^2} = {({x_0} - 2)^2} + {y_0}^2\)

Vì \(A \in \left( E \right) \Rightarrow {{{x_0}^2} \over 4} + {y_0}^2 = 1 \Rightarrow {y_0}^2 = 1 - {{{x_0}^2} \over 4}\,\,\,\,\left( 1 \right)\)

Vì \(AB = AC \Rightarrow {({x_0} - 2)^2} + {y_0}^2 = 4{y_0}^2\,\,\,\,\,\left( 2 \right)\)

Thay (1) vào (2) và rút gọn ta được :

\(7{x_0}^2 - 16{x_0} + 4 = 0 \Leftrightarrow \left[ \matrix{  {x_0} = 2 \hfill \cr   {x_0} = {2 \over 7} \hfill \cr}  \right.\)

Với \({x_0} = 2 \Rightarrow {y_0} = 0\,\,(L)\) vì trùng với điểm C.

Với \({x_0} = {2 \over 7} \Rightarrow {y_0} =  \pm {{4\sqrt 3 } \over 7}\).

Vậy, \(A\left( {{2 \over 7};{{4\sqrt 3 } \over 7}} \right),\,\,B\left( {{2 \over 7}; - {{4\sqrt 3 } \over 7}} \right)\) hoặc \(A\left( {{2 \over 7}; - {{4\sqrt 3 } \over 7}} \right),\,\,B\left( {{2 \over 7};{{4\sqrt 3 } \over 7}} \right)\). 

Chọn: C.

Phương pháp giải:

Gọi \(M\left( {{x_0};{y_0}} \right) \in \left( E \right)\), tính \(d\left( {M;\left( D \right)} \right) = {{\left| {{x_0} - 2{y_0} + 12} \right|} \over {\sqrt {{1^2} + {2^2}} }}\)

Sử dụng các bất đẳng thức \(\left| {a + b} \right| \le \left| a \right| + \left| b \right|\), dấu bằng xảy ra \( \Leftrightarrow a.b \ge 0\) và BĐT Bunhia-copxki: \(\left( {{a^2} + {b^2}} \right)\left( {{x^2} + {y^2}} \right) \ge {\left( {ax + by} \right)^2}\), dấu bằng xảy ra \( \Leftrightarrow {a \over x} = {b \over y}\)

Lời giải chi tiết:

Gọi \(M({x_0};{y_0}) \in (E) \Rightarrow \,\,{{{x_0}^2} \over {25}} + {{{y_0}^2} \over 9} = 1\).

Khoảng cách từ M đến D:

\(\eqalign{  & d(M,D) = {{\left| {{x_0} - 2{y_0} + 12} \right|} \over {\sqrt {{1^2} + {2^2}} }} = {{\left| {{x_0} - 2{y_0} + 12} \right|} \over {\sqrt 5 }} \le {{\left| {{x_0} - 2{y_0}} \right| + 12} \over {\sqrt 5 }} = {{\left| {5.{{{x_0}} \over 5} + \left( { - 6} \right){{{y_0}} \over 3}} \right| + 12} \over {\sqrt 5 }} \le {{\sqrt {({5^2} + {6^2})\left( {{{{x_0}^2} \over {25}} + {{{y_0}^2} \over 9}} \right)}  + 12} \over {\sqrt 5 }}  \cr   &  = {{\sqrt {(25 + 36).1}  + 12} \over {\sqrt 5 }} = {{\sqrt {61}  + 12} \over {\sqrt 5 }} \cr} \).

Vậy,

\(d{(M,D)_{\max }} = {{\sqrt {61}  + 12} \over {\sqrt 5 }} \Leftrightarrow \left\{ \matrix{ \left( {{x_0} - 2{y_0}} \right).12 \ge 0 \hfill \cr   {{{x_0}^2} \over {25}} + {{{y_0}^2} \over 9} = 1 \hfill \cr   {{{{{x_0}} \over 5}} \over 5} = {{{{{y_0}} \over 3}} \over { - 6}} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_0} - 2{y_0} \ge 0 \hfill \cr   {{{x_0}^2} \over {25}} + {{{y_0}^2} \over 9} = 1 \hfill \cr   18{x_0} + 25{y_0} = 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_0} - 2{y_0} \ge 0 \hfill \cr   {{{x_0}^2} \over {25}} + {{{y_0}^2} \over 9} = 1 \hfill \cr   {x_0} =  - {{25} \over {18}}{y_0} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_0} - 2{y_0} \ge 0 \hfill \cr   {{{{\left( { - {{25} \over {18}}{y_0}} \right)}^2}} \over {25}} + {{{y_0}^2} \over 9} = 1 \hfill \cr   {x_0} =  - {{25} \over {18}}{y_0} \hfill \cr}  \right.\)

\( \Leftrightarrow \left\{ \matrix{  {x_0} - 2{y_0} \ge 0 \hfill \cr   {y_0}^2 = {{324} \over {661}} \hfill \cr   {x_0} =  - {{25} \over {18}}{y_0} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_0} - 2{y_0} \ge 0 \hfill \cr   {y_0} =  \pm \sqrt {{{324} \over {661}}}  \hfill \cr   {x_0} =  - {{25} \over {18}}{y_0} \hfill \cr}  \right. \Leftrightarrow \left[ \matrix{  \left\{ \matrix{  {x_0} =  - {{25} \over {18}}\sqrt {{{324} \over {661}}}  \hfill \cr   {y_0} = \sqrt {{{324} \over {661}}}  \hfill \cr}  \right.\,\,(L) \hfill \cr   \left\{ \matrix{  {x_0} = {{25} \over {18}}\sqrt {{{324} \over {661}}}  \hfill \cr   {y_0} =  - \sqrt {{{324} \over {661}}}  \hfill \cr}  \right.\,\,(TM) \hfill \cr}  \right.\)

Khi đó, \(M\left( {{{25} \over {18}}\sqrt {{{324} \over {661}}} ; - \sqrt {{{324} \over {661}}} } \right)\)

Chọn: C

Lời giải chi tiết:

Ta có: \({S_{ABC}} = {1 \over 2}.d(A;BC).BC = {1 \over 2}d(A,\Delta ).BC\)

Nhận xét: \({S_{ABC}}\) đạt GTLN khi và chỉ khi \(d(A;\Delta )\) lớn nhất.

\(A({x_0};{y_0}) \in (E) \Rightarrow \,\,\,{{{x_0}^2} \over 8} + {{{y_0}^2} \over 4} = 1\).

Khoảng cách từ A đến D:

\(\eqalign{  & d(A,\Delta ) = {{\left| {{x_0} - \sqrt 2 {y_0} + 2} \right|} \over {\sqrt {{1^2} + {{\left( {\sqrt 2 } \right)}^2}} }} = {{\left| {{x_0} - \sqrt 2 {y_0} + 2} \right|} \over {\sqrt 3 }} \le {{\left| {{x_0} - \sqrt 2 {y_0}} \right| + 2} \over {\sqrt 3 }} = {{\left| {2\sqrt 2 .{{{x_0}} \over {2\sqrt 2 }} + \left( { - 2\sqrt 2 } \right).{{{y_0}} \over 2}} \right| + 2} \over {\sqrt 3 }}  \cr   &  \le {{\sqrt {\left[ {{{\left( {2\sqrt 2 } \right)}^2} + {{\left( { - 2\sqrt 2 } \right)}^2}} \right]\left( {{{{x_0}^2} \over 8} + {{{y_0}^2} \over 4}} \right)}  + 2} \over {\sqrt 3 }} = {{\sqrt {16.1}  + 2} \over {\sqrt 3 }} = {6 \over {\sqrt 3 }} = 2\sqrt 3  \cr} \)

\(\eqalign{  & d{(A;\Delta )_{{\rm{Max}}}} = 2\sqrt 3  \Leftrightarrow \left\{ \matrix{  \left( {{x_0} - \sqrt 2 {y_0}} \right).2 \ge 0 \hfill \cr   {{{x_0}^2} \over 8} + {{{y_0}^2} \over 4} = 1 \hfill \cr   {{{{{x_0}} \over {2\sqrt 2 }}} \over {2\sqrt 2 }} = {{{{{y_0}} \over 2}} \over { - 2\sqrt 2 }} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_0} - \sqrt 2 {y_0} \ge 0 \hfill \cr   {{{x_0}^2} \over 8} + {{{y_0}^2} \over 4} = 1 \hfill \cr   {x_0} =  - \sqrt 2 {y_0} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_0} - \sqrt 2 {y_0} \ge 0 \hfill \cr   {{2{y_0}^2} \over 8} + {{{y_0}^2} \over 4} = 1 \hfill \cr   {x_0} =  - \sqrt 2 {y_0} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_0} - \sqrt 2 {y_0} \ge 0 \hfill \cr   {y_0}^2 = 2 \hfill \cr   {x_0} =  - \sqrt 2 {y_0} \hfill \cr}  \right.  \cr   &  \Leftrightarrow \left\{ \matrix{  {x_0} - \sqrt 2 {y_0} \ge 0 \hfill \cr   {y_0} =  \pm \sqrt 2  \hfill \cr   {x_0} =  - \sqrt 2 {y_0} \hfill \cr}  \right. \Leftrightarrow \left[ \matrix{  \left\{ \matrix{  {x_0} = 2 \hfill \cr   {y_0} =  - \sqrt 2  \hfill \cr}  \right.\,(TM) \hfill \cr   \left\{ \matrix{  {x_0} =  - 2 \hfill \cr   {y_0} = \sqrt 2  \hfill \cr}  \right.(L) \hfill \cr}  \right. \cr} \)

Khi đó, \(A\left( {2; - \sqrt 2 } \right)\)

Chọn: A

Phương pháp giải:

Gọi \(A({x_0};{y_0}) \in \left( E \right)\,\,\left( {{y_0} > 0} \right)\), xác định điểm B đối xứng với A qua trục Ox.

Tam giác \(AB{F_1}\) đều \( \Leftrightarrow AB = A{F_1}\)

Lời giải chi tiết:

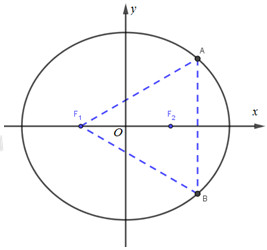
Giả sử \(A({x_0};{y_0}),\,\,{y_0} > 0\). Do A, B đối xứng nhau qua Ox nên \(B({x_0}; - {y_0})\).

\((E):13{x^2} + 16{y^2} = 208 \Leftrightarrow {{{x^2}} \over {16}} + {{{y^2}} \over {13}} = 1 \Rightarrow a = 4,\,\,b = \sqrt {13}  \Rightarrow c = \sqrt 3 \)

\( \Rightarrow {F_1}\left( { - \sqrt 3 ;0} \right)\)

Ta có: \(A{B^2} = 4{y_0}^2,\,\,\,A{F_1}^2 = {\left( {{x_0} + \sqrt 3 } \right)^2} + {y_0}^2\)

Vì \(A \in \left( E \right) \Rightarrow 13{x_0}^2 + 16{y_0}^2 = 208 \Rightarrow {y_0}^2 = 13 - {{13} \over {16}}{x_0}^2\,\,(1)\)

Vì tam giác \(AB{F_1}\) là tam giác đều \( \Rightarrow AB = A{F_1} \Rightarrow {\left( {{x_0} + \sqrt 3 } \right)^2} + {y_0}^2 = 4{y_0}^2\,\,\,(2)\)

Thay (1) vào (2) ta được : \({\left( {{x_0} + \sqrt 3 } \right)^2} + 13 - {{13} \over {16}}{x_0}^2 = 4\left( {13 - {{13} \over {16}}{x_0}^2} \right) \Leftrightarrow {{55} \over {16}}{x_0}^2 + 2\sqrt 3 {x_0} - 36 = 0 \Leftrightarrow \left[ \matrix{  {x_0} = {{8\sqrt 3 } \over 5} \hfill \cr   {x_0} = {{ - 24\sqrt 3 } \over {11}} \hfill \cr}  \right.\)

+) \({x_0} = {{8\sqrt 3 } \over 5} \Rightarrow \left[ \matrix{  {y_0} = {{13} \over 5} \hfill \cr   {y_0} =  - {{13} \over 5}\,(L) \hfill \cr}  \right. \Rightarrow A\left( {{{8\sqrt 3 } \over 5};{{13} \over 5}} \right),\,B\left( {{{8\sqrt 3 } \over 5}; - {{13} \over 5}} \right)\,\)

 +) \({x_0} = {{ - 24\sqrt 3 } \over {11}} \Rightarrow \left[ \matrix{  {y_0} = {{13} \over {11}} \hfill \cr   {y_0} =  - {{13} \over {11}}\,(L) \hfill \cr}  \right. \Rightarrow A\left( { - {{24\sqrt 3 } \over {11}};{{13} \over {11}}} \right),\,B\left( { - {{24\sqrt 3 } \over {11}}; - {{13} \over {11}}} \right)\,\)

Vậy, \(A\left( {{{8\sqrt 3 } \over 5};{{13} \over 5}} \right),\,B\left( {{{8\sqrt 3 } \over 5}; - {{13} \over 5}} \right)\,\) hoặc \(A\left( { - {{24\sqrt 3 } \over {11}};{{13} \over {11}}} \right),\,B\left( { - {{24\sqrt 3 } \over {11}}; - {{13} \over {11}}} \right)\,\).

Chọn: B.

Phương pháp giải:

Phương trình chính tắc của Elip có dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \({a^2} - {b^2} = {c^2}\)

Trong đó: trục lớn \({A_1}{A_2} = 2a\); trục nhỏ \({B_1}{B_2} = 2b\); tiêu cự \({F_1}{F_2} = 2c\)

Lời giải chi tiết:

Elip có tiêu cự bằng  \(16 \Rightarrow 2c = 16 \Rightarrow c = 8\)

Elip có trục lớn bằng  \(20 \Rightarrow 2a = 20 \Rightarrow a = 10.\)

\( \Rightarrow {b^2} = {a^2} - {c^2} = {10^2} - {8^2} = 36\)

Vậy phương trình chính tắc của Elip là: \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)

Chọn A.

Lời giải chi tiết:

* Giả sử \(\left( E \right):\,\,\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\). \(M \in \left( E \right) \Rightarrow \dfrac{9}{{{b^2}}} = 1 \Rightarrow {b^2} = 9\,\,\left( 1 \right)\).

* \({F_2}\left( {4;0} \right) \Rightarrow c = 4 \Rightarrow {c^2} = 16 \Rightarrow {a^2} - {b^2} = 16\,\,\left( 2 \right)\)

* Giải hệ \(\left\{ \begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{b^2} = 9\\{a^2} = 25\end{array} \right. \Rightarrow \dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1\).

Chọn A.

Lời giải chi tiết:

* Giả sử \(\left( E \right):\,\,\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\).

\(\begin{array}{l}*\,\,M \in \left( E \right) \Rightarrow \dfrac{{16}}{{{a^2}}} = 1 \Rightarrow {a^2} = 16\,\,\left( 1 \right)\\*\,\,N \in \left( E \right) \Rightarrow \dfrac{9}{{{b^2}}} = 1 \Rightarrow {b^2} = 9\,\,\left( 2 \right)\end{array}\).

Chọn B.

Lời giải chi tiết:

* Trục lớn bằng 16 \( \Rightarrow 2a = 16 \Rightarrow a = 8\).

* \(e = \dfrac{c}{a} = \dfrac{5}{8}\). Với \(a = 8 \Rightarrow c = 5 \Rightarrow {c^2} = 25\).

\( \Rightarrow {a^2} - {b^2} = 25 \Rightarrow {b^2} = {a^2} - 25 = 64 - 25 = 39\).

* Phương trình \(\left( E \right):\,\,\dfrac{{{x^2}}}{{64}} + \dfrac{{{y^2}}}{{39}} = 1\).

Chọn C.

Lời giải chi tiết:

* Trục lớn có đỉnh \(A\left( {4;0} \right)\) \( \Rightarrow a = 4 \Rightarrow {a^2} = 16\)  (1).

* \(e = \dfrac{c}{a} = \dfrac{{\sqrt 7 }}{4}\). Với \( = 4 \Rightarrow c = \sqrt 7  \Rightarrow {c^2} = 7\).

\( \Rightarrow {a^2} - {b^2} = 7 \Rightarrow {b^2} = {a^2} - 7 = 9\).

* Phương trình \(\left( E \right):\,\,\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1\).

Chọn B.

Lời giải chi tiết:

* Trục bé bằng 8 \( \Rightarrow 2b = 8 \Rightarrow b = 4 \Rightarrow {b^2} = 16\).

* Tiêu cự bằng 4 \( \Rightarrow 2c = 4 \Rightarrow c = 2 \Rightarrow {c^2} = 4\)

\( \Rightarrow {a^2} - {b^2} = 4 \Rightarrow {a^2} = {b^2} + 4 = 20\).

* Phương trình \(\left( E \right):\,\,\dfrac{{{x^2}}}{{20}} + \dfrac{{{y^2}}}{{16}} = 1\).

Chọn A.

Lời giải chi tiết:

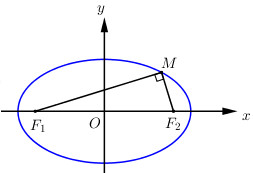
* \({c^2} = {a^2} - {b^2} = 25 - 2 = 23 \Rightarrow c = \sqrt {23} \)

\( \Rightarrow {F_1}\left( { - \sqrt {23} ;0} \right);\,\,{F_2}\left( {\sqrt {23} ;0} \right)\)

* Giả sử \(M\left( {{x_M};{y_M}} \right) \in \left( E \right) \Rightarrow \dfrac{{x_M^2}}{{25}} + \dfrac{{y_M^2}}{2} = 1\,\,\,\left( 1 \right)\)

\(*\,\,\left\{ \begin{array}{l}\overrightarrow {{F_1}M}  = \left( {{x_M} + \sqrt {23} ;{y_M}} \right)\\\overrightarrow {{F_2}M}  = \left( {{x_M} - \sqrt {23} ;{y_M}} \right)\end{array} \right.;\,\,\overrightarrow {{F_1}M} .\overrightarrow {{F_2}M}  = 0 \Leftrightarrow x_M^2 + y_M^2 = 23\,\,\left( 2 \right)\)

* Giải hệ \(\left\{ \begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x_M^2 = \dfrac{{525}}{{23}}\\y_M^2 = \dfrac{4}{{23}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \sqrt {\dfrac{{523}}{{23}}} \\y = \sqrt {\dfrac{4}{{23}}} \end{array} \right. \Rightarrow M\left( {\sqrt {\dfrac{{523}}{{23}}} ;\sqrt {\dfrac{4}{{23}}} } \right)\).

Chọn A.

Lời giải chi tiết:

* Ta có \(a = 3,\,\,b = 1 \Rightarrow {c^2} = {a^2} - {b^2} = 8 \Rightarrow c = \sqrt 8  \Rightarrow e = \dfrac{c}{a} = \dfrac{{\sqrt 8 }}{3}\).

* Giả sử \(M\left( {{x_M};{y_M}} \right) \in \left( E \right) \Rightarrow \dfrac{{x_M^2}}{9} + \dfrac{{y_M^2}}{1} = 1\,\,\,\left( 1 \right)\).

* \(M{F_1} = 2M{F_2} \Leftrightarrow a + e{x_M} = 2\left( {a - e{x_M}} \right) \Rightarrow 3e{x_M} = a\)

\( \Rightarrow {x_M} = \dfrac{e}{{3a}} = \dfrac{3}{{3.\dfrac{{\sqrt 8 }}{3}}} = \dfrac{3}{{\sqrt 8 }}\,\,\left( 2 \right)\)

* Giải hệ \(\left\{ \begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array} \right. \Rightarrow M\left( {\dfrac{{3\sqrt 2 }}{4};\dfrac{{\sqrt {14} }}{4}} \right)\).

Chọn A.

Lời giải chi tiết:

* Giải hệ \(\left\{ \begin{array}{l}\left( d \right)\\\left( E \right)\end{array} \right.\). Từ \(\left( d \right) \Rightarrow x = 2y + 2\,\,\left( * \right)\). Thay vào \(\left( E \right)\) ta có:

\(5{x^2} + 4{y^2} = 20 \Rightarrow 5{\left( {2y + 2} \right)^2} + 4{y^2} = 20 \Leftrightarrow \left[ \begin{array}{l}y = 0\\y =  - \dfrac{5}{3}\end{array} \right.\)

* \(\left[ \begin{array}{l}y = 0 \Rightarrow x = 2 \Rightarrow A\left( {2;0} \right)\\y =  - \dfrac{5}{3} \Rightarrow x =  - \dfrac{4}{3} \Rightarrow B\left( { - \dfrac{4}{3}; - \dfrac{5}{3}} \right)\end{array} \right. \Rightarrow P =  - 1\)

Chọn B.

Phương pháp giải:

Phương trình chính tắc của elip có dạng \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\). Tìm \(a,b\).

Lời giải chi tiết:

Phương trình elip cần tìm có dạng  \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)

Diện tích hình chữ nhật cơ sở  bằng  \(4ab\).

Theo bài ra ta có \(4ab = 8 \Leftrightarrow ab = 2 \Leftrightarrow {a^2}{b^2} = 4\)

Elip có \(e = {{\sqrt {12} } \over 4}\) suy ra \({c \over a} = {{\sqrt {12} } \over 4}\). Vì \(c,a > 0\) nên ta có \({{{c^2}} \over {{a^2}}} = {{12} \over {16}} = {3 \over 4} \Leftrightarrow 3{a^2} - 4{c^2} = 0\)

Mặt khác ta có: \({a^2} - {b^2} = {c^2}\)

Ta có hệ phương trình \(\left\{ \matrix{  {a^2}{b^2} = 4 \hfill \cr   3{a^2} - 4{c^2} = 0 \hfill \cr   {a^2} - {b^2} = {c^2} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {a^2}{b^2} = 4 \hfill \cr   {a^2} - {b^2} = {3 \over 4}{a^2} \hfill \cr   3{a^2} = 4{c^2} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {a^2}{b^2} = 4 \hfill \cr   {a^2} - 4{b^2} = 0 \hfill \cr   3{a^2} = 4{c^2} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {a^2} = 4 \hfill \cr   {b^2} = 1 \hfill \cr   {c^2} = 3 \hfill \cr}  \right.\)

Vậy elip có phương trình là \({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\).

Đáp án: B

Phương pháp giải:

Giả sử \(M\left( {{x_0};{y_0}} \right)\). Biến đổi tương đương  biểu thức \(2\overrightarrow {AM}  + 5\overrightarrow {MB}  = \vec 0\), sau đó làm mất tham số \(\alpha \). 

Lời giải chi tiết:

Giả sử \(M\left( {{x_0};{y_0}} \right)\) ta có:

\(\eqalign{  & \overrightarrow {AM}  = \left( {{x_0} - 3\cos \alpha ;{y_0}} \right)  \cr   & \overrightarrow {MB}  = \left( { - {x_0};2\sin \alpha  - {y_0}} \right) \cr} \)

Suy ra  \(2\overrightarrow {AM}  + 5\overrightarrow {MB}  = \vec 0 \Leftrightarrow \left\{ \matrix{  2\left( {{x_0} - 3\cos \alpha } \right) - 5{x_0} = 0 \hfill \cr   2{y_0} + 5\left( {2\sin \alpha  - {y_0}} \right) = 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{   - 3{x_0} - 6\cos \alpha  = 0 \hfill \cr   10\sin \alpha  - 3{y_0} = 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  \cos \alpha  =  - {1 \over 2}{x_0} \hfill \cr   \sin \alpha  = {3 \over {10}}{y_0} \hfill \cr}  \right.\)

Mặt khác ta có \({\cos ^2}\alpha  + {\sin ^2}\alpha  = 1\) nên ta có: \({{x_0^2} \over 4} + {{9y_0^2} \over {100}} = 1\)

Đáp án: A.

Phương pháp giải:

Xác định mối quan hệ giữa A và B để tam giác OAB cân tại O.

Gọi điểm \(A({x_0};{y_0}) \in \left( E \right)\,\,\left( {{x_0} > 0} \right)\)

Gọi H là trung điểm của AB \( \Rightarrow \) tọa độ điểm H.

\({S_{\Delta OAB}} = {1 \over 2}OH.AB\), sử dụng BĐT Cô si cho hai số không âm: \(\sqrt {ab}  \le {{{a^2} + {b^2}} \over 2}\), dấu bằng xảy ra \( \Leftrightarrow a = b\).

Lời giải chi tiết:

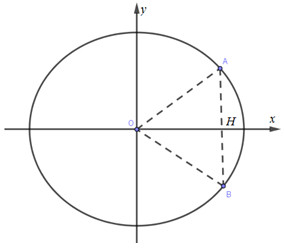
Tam giác OAB cân tại O, A và B thuộc (E) , có hoành độ dương, suy ra: A đối xứng với B qua Ox.

Gọi \(A({x_0};{y_0}) \Rightarrow B({x_0}; - {y_0});{\rm{ (}}{{\rm{x}}_0} > 0)\).

\(A \in (E):{{{x^2}} \over 4} + {{{y^2}} \over 1} = 1 \Rightarrow {{{x_0}^2} \over 4} + {{{y_0}^2} \over 1} = 1 \Rightarrow \left| {{y_0}} \right| = {{\sqrt {4 - {x_0}^2} } \over 2}\)

Ta có \(AB = 2\left| {{y_0}} \right| = \sqrt {4 - {x_0}^2} \)

Gọi H là trung điểm AB thì  \(H\left( {{x_0};0} \right)\)

\( \Rightarrow OH = {x_0} \Rightarrow {S_{OAB}} = {1 \over 2}.OH.AB = {1 \over 2}{x_0}.\sqrt {4 - {x_0}^2}  = {1 \over 2}\sqrt {{x_0}^2(4 - {x_0}^2)}  \le {1 \over 2}.{{{x_0}^2 + 4 - {x_0}^2} \over 2} = 1\).

Đẳng thức xảy ra khi \(x_0^2 = 4 - x_0^2 \Leftrightarrow {x_0} = \sqrt 2  \Rightarrow {y_0} =  \pm {{\sqrt 2 } \over 2}\).

Vậy \(A\left( {\sqrt 2 ;{{\sqrt 2 } \over 2}} \right);B\left( {\sqrt 2 ; - {{\sqrt 2 } \over 2}} \right)\) hoặc \(A\left( {\sqrt 2 ; - {{\sqrt 2 } \over 2}} \right);B\left( {\sqrt 2 ;{{\sqrt 2 } \over 2}} \right)\).

Chọn: A.

Phương pháp giải:

Cho elip \(\left( E \right):\,\,\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) và đường thẳng \(d:Ax + By + C = 0\).

Điều kiện để đường thẳng \(d\) tiếp xúc với \(\left( E \right)\) là \({A^2}{a^2} + {B^2}{b^2} = {C^2}.\)

Lời giải chi tiết:

Điểm \(M\) chuyển động trên trục \(Ox\) và điểm \(N\) chuyển động trên trục \(Oy\).

\( \Rightarrow M\left( {m;\,\,0} \right),\,N\left( {0;\,\,n} \right)\) với \(m > 0,\,\,n > 0\).

Phương trình đường thẳng \(MN\): \(\frac{x}{m} + \frac{y}{n} = 1\)

Để đường thẳng \(MN\) tiếp xúc với elip \(\left( E \right):\,\,\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\) thì: \({\left( {\frac{1}{m}} \right)^2} \cdot 16 + {\left( {\frac{1}{n}} \right)^2} \cdot 9 = 1\)

Ta có: \(M\left( {m;\,\,0} \right),\,\,N\left( {0;\,\,n} \right)\)\( \Rightarrow \overrightarrow {MN}  = \left( { - m;\,\,n} \right)\)\( \Rightarrow MN = \sqrt {{m^2} + {n^2}} \)

\( \Rightarrow M{N^2} = {m^2} + {n^2} = \left( {{m^2} + {n^2}} \right).1\)\( = \left( {{m^2} + {n^2}} \right) \cdot \left( {\frac{{16}}{{{m^2}}} + \frac{9}{{{n^2}}}} \right)\)\( = 25 + 16 \cdot \frac{{{n^2}}}{{{m^2}}} + 9 \cdot \frac{{{m^2}}}{{{n^2}}}\)

Áp dụng bất đẳng thức Cô-si ta có:

\(M{N^2} = 25 + 16 \cdot \frac{{{n^2}}}{{{m^2}}} + 9 \cdot \frac{{{m^2}}}{{{n^2}}} \ge 25 + 2\sqrt {16 \cdot \frac{{{n^2}}}{{{m^2}}} \cdot 9 \cdot \frac{{{m^2}}}{{{n^2}}}}  = 49\)

\( \Rightarrow M{N^2} \ge 49\)

\( \Rightarrow MN \ge 7\)

Dấu “\( = \)” xảy ra khi \(\left\{ \begin{array}{l}\frac{{16{n^2}}}{{{m^2}}} = \frac{{9{m^2}}}{{{n^2}}}\\{m^2} + {n^2} = 49\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 2\sqrt 7 \\n = \sqrt {21} \end{array} \right.\) (thõa mãn điều kiện)

Vậy \(M\left( {2\sqrt 7 ;\,\,0} \right)\) và \(N\left( {0;\,\,\sqrt {21} } \right)\) thì \(MN\) đạt giá trị nhỏ nhất bằng \(7.\)

Chọn B.

Phương pháp giải:

+) Gọi \(B\left( {{x_0};\,{y_0}} \right),\,\,C\left( {{x_0};\, - {y_0}} \right)\) với \(\,{y_0} > 0\).

+) Vì \(A\) là một điểm nằm trên trục \(Ox\) nên tam giác \(ABC\) cân tại \(A\).

+) Xác định khoảng cách từ \(A\) đến đường thẳng \(BC\).

+) Để \(\Delta ABC\) đều thì \(\tan {60^0} = \frac{{d\left( {A,\,\,BC} \right)}}{{\frac{{BC}}{2}}}\).

Lời giải chi tiết:

Giả sử \(B\left( {{x_0};\,{y_0}} \right),\,\,C\left( {{x_0};\, - {y_0}} \right)\) với \(\,{y_0} > 0\).

Vì \(B,\,\,C\) nằm trên elip \(\left( E \right)\) nên ta có: \(\frac{{x_0^2}}{9} + \frac{{y_0^2}}{3} = 1 \Leftrightarrow x_0^2 + 3y_0^2 = 9\,\,\,\,\,\,\,\,\,\left( 1 \right)\)

\(B\left( {{x_0};\,{y_0}} \right),\,\,C\left( {{x_0};\, - {y_0}} \right) \Rightarrow \overrightarrow {BC}  = \left( {{x_0} - {x_0};\, - {y_0} - {y_0}} \right) = \left( {0;\,\, - 2{y_0}} \right)\)

Ta có: \(\left( {BC} \right):\,\,\left\{ \begin{array}{l}{\mathop{\rm qua}\nolimits} \,B\left( {{x_0};{y_0}} \right)\\{{\vec n}_{BC}} = \left( {2{y_0};\,\,0} \right)\end{array} \right.\)

\( \Rightarrow 2{y_0}\left( {x - {x_0}} \right) + 0.\left( {y - {y_0}} \right) = 0\)

\( \Leftrightarrow 2{y_0}\left( {x - {x_0}} \right) = 0\)

\( \Leftrightarrow x - {x_0} = 0\)

Phương trình đường thẳng \(BC\) là: \(x - {x_0} = 0\)

Vì \(A\left( {3;\,\,0} \right)\) nên \(A \in Ox\), \(B\) và \(C\) đối xứng qua \(Ox\) nên \(\Delta ABC\) cân tại \(A\).

Để \(\Delta ABC\) là tam giác đều thì \(\tan {60^0} = \frac{{d\left( {A,\,\,BC} \right)}}{{\frac{{BC}}{2}}}\)

\( \Rightarrow \tan {60^0} = \frac{{\left| {3 - {x_0}} \right|}}{{\frac{{2{y_0}}}{2}}} \Leftrightarrow \sqrt 3  = \frac{{\left| {3 - {x_0}} \right|}}{{{y_0}}} \Leftrightarrow \left| {3 - {x_0}} \right| = {y_0}\sqrt 3  \Leftrightarrow {y_0} = \frac{{\left| {3 - {x_0}} \right|}}{{\sqrt 3 }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)

Thay \(\left( 2 \right)\) vào \(\left( 1 \right)\) ta được:

\(x_0^2 + 3.{\left( {\frac{{\left| {3 - {x_0}} \right|}}{{\sqrt 3 }}} \right)^2} = 9\)\( \Leftrightarrow x_0^2 + {\left( {3 - {x_0}} \right)^2} = 9\)\( \Leftrightarrow x_0^2 + 9 - 6{x_0} + x_0^2 = 9\)\( \Leftrightarrow 2x_0^2 - 6{x_0} = 0 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 0\\{x_0} = 3\end{array} \right.\)

+) Với \({x_0} = 0 \Rightarrow {y_0} = \sqrt 3  \Rightarrow B\left( {0;\,\,\sqrt 3 } \right),\,\,C\left( {0;\,\, - \sqrt 3 } \right)\)

+) Với \({x_0} = 3 \Rightarrow {y_0} = 0 \Rightarrow \)Loại

Vậy \(B\left( {0;\,\,\sqrt 3 } \right),\,\,C\left( {0;\,\, - \sqrt 3 } \right)\).

Chọn  A.