Phương pháp giải:

Gọi biến cố A: “Lấy được hai quả cầu mà tích hai số trên hai quả cầu chia hết cho 10”.

TH1: Hai quả cầu lấy được có đúng một quả mang số chia hết cho 10

TH2: Hai quả cầu lấy dược đều là số chia hết cho 10

TH3: Hai quả cầu lấy được có 1 quả cầu là số chia hết cho 2 (nhưng không chia hết cho 5) và 1 quả cầu mang số chia hết cho 5 (nhưng không chia hết cho 2)

Xác suất của biến cố A là: \(P\left( A \right) = \dfrac{{{n_A}}}{{{n_\Omega }}}.\)

Lời giải chi tiết:

Số cách lấy ngẫu nhiên hai quả cầu trong số 60 quả cầu đã cho là: \(C_{60}^2\) cách lấy.

Gọi biến cố A: “Lấy được hai quả cầu mà tích hai số trên hai quả cầu chia hết cho 10”.

TH1: Hai quả cầu lấy được có đúng một quả mang số chia hết cho 10

\( \Rightarrow \) Có \(C_6^1.C_{54}^1\) cách lấy.

TH2: Hai quả cầu lấy dược đều là số chia hết cho 10

\( \Rightarrow \) Có \(C_6^2\) cách lấy.

TH3: Hai quả cầu lấy được có 1 quả cầu là số chia hết cho 2 (nhưng không chia hết cho 5) và 1 quả cầu mang số chia hết cho 5 (nhưng không chia hết cho 2)

\( \Rightarrow \) Có \(\left( {30 - 6} \right)\left( {12 - 6} \right) = 24.6 = 144\) cách lấy.

\( \Rightarrow {n_A} = C_6^1.C_{54}^1 + C_6^2 + 144 = 483\) cách lấy.

\( \Rightarrow P\left( A \right) = \dfrac{{483}}{{C_{60}^2}} = \dfrac{{161}}{{590}}.\)

Chọn B.

Phương pháp giải:

- Gọi số tự nhiên có 8 chữ số khác nhau là \(X = \overline {{a_1}{a_2}...{a_8}} \,\,\left( {{a_1} \ne 0} \right)\). Tìm số các số tự nhiên có 8 chữ số khác nhau.

- Tính số phần tử của không gian mẫu.

- Gọi M là biến cố: “số tự nhiên được chọn chia hết cho 25”. Phân tích \(X = \overline {{a_1}{a_2}...{a_8}}  = {a_1}{.10^7} + {a_2}{.10^6} + {a_3}{.10^5} + {a_4}{.10^4} + {a_5}{.10^3} + {a_6}{.10^2} + {a_7}.10 + {a_8}\), chứng minh \(X\,\, \vdots \,\,25 \Leftrightarrow 10{a_7} + {a_8}\,\, \vdots \,\,25\).

- Xác định các cặp số \(\left( {{a_7};{a_8}} \right)\) thỏa mãn \(10{a_7} + {a_8}\,\, \vdots \,\,25\), từ đó tính số phần tử của biến cố M.

- Tính xác suất của biến cố M: \(P\left( M \right) = \dfrac{{n\left( M \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Gọi số tự nhiên có 8 chữ số khác nhau là \(X = \overline {{a_1}{a_2}...{a_8}} \,\,\left( {{a_1} \ne 0} \right)\).

Số cách chọn \({a_1}\): 9 cách.

Số cách chọn 7 chữ số còn lại: \(A_9^7\) cách.

\( \Rightarrow \) Tập hợp A có \(9.A_9^7\) số tự nhiên có 8 chữ số khác nhau.

Chọn ngẫu nhiên 1 số thuộc A \( \Rightarrow \) Không gian mẫu \(n\left( \Omega  \right) = C_{9.A_9^7}^1 = 9.A_9^7\).

Gọi M là biến cố: “số tự nhiên được chọn chia hết cho 25”.

Ta có: \(X = \overline {{a_1}{a_2}...{a_8}}  = {a_1}{.10^7} + {a_2}{.10^6} + {a_3}{.10^5} + {a_4}{.10^4} + {a_5}{.10^3} + {a_6}{.10^2} + {a_7}.10 + {a_8}\).

Vì \({10^k}\,\, \vdots \,\,25\,\,\forall k = \overline {2;8} ,\,\,k \in \mathbb{N}\) nên \(X\,\, \vdots \,\,25 \Leftrightarrow 10{a_7} + {a_8}\,\, \vdots \,\,25\).

Do \({a_7},\,\,{a_8} \in \mathbb{N},\,\,0 \le {a_7},\,\,{a_8} \le 9\), \({a_7} \ne {a_8}\)  nên \(0 < 10{a_7} + {a_8} \le 99\).

\( \Rightarrow 10{a_7} + {a_8} \in \left\{ {25;50;75} \right\}\).

Lại có số chia hết cho 25 là số có tận cùng là 0 hoặc 5 nên \({a_8} \in \left\{ {0;5} \right\}\).

TH1: \(10{a_7} + {a_8} = 25 \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{a_8} = 0\\{a_7} = \dfrac{{25}}{{10}}\end{array} \right.\,\,\left( {KTM} \right)\\\left\{ \begin{array}{l}{a_8} = 5\\{a_7} = 2\end{array} \right.\,\,\left( {TM} \right)\end{array} \right.\).

\( \Rightarrow \) Có 1 cách chọn \({a_7},\,\,{a_8}\).

Số cách chọn \({a_1}\): 7 cách \(\left( {{a_1} \ne 0,\,\,{a_1} \ne {a_7},\,{a_8}} \right)\).

Số cách chọn 5 chữ số còn lại: \(A_7^5\) cách.

\( \Rightarrow \) Có \(7.A_7^5\) số.

TH2:  \(10{a_7} + {a_8} = 50 \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{a_8} = 0\\{a_7} = 5\end{array} \right.\,\,\left( {TM} \right)\\\left\{ \begin{array}{l}{a_8} = 5\\{a_7} = \dfrac{{45}}{{10}}\end{array} \right.\,\,\left( {KTM} \right)\end{array} \right.\).

\(\) Có 1 cách chọn \({a_7},\,\,{a_8}\).

Số cách chọn \({a_1}\): 8 cách \(\left( {{a_1} \ne {a_7},\,{a_8}} \right)\).

Số cách chọn 5 chữ số còn lại: \(A_7^5\) cách.

\( \Rightarrow \) Có \(8.A_7^5\) số.

TH3:  \(10{a_7} + {a_8} = 75 \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{a_8} = 0\\{a_7} = \dfrac{{75}}{{10}}\end{array} \right.\,\,\left( {KTM} \right)\\\left\{ \begin{array}{l}{a_8} = 5\\{a_7} = 7\end{array} \right.\,\,\left( {TM} \right)\end{array} \right.\).

\( \Rightarrow \) Có 1 cách chọn \({a_7},\,\,{a_8}\).

Số cách chọn \({a_1}\): 7 cách \(\left( {{a_1} \ne 0,\,\,{a_1} \ne {a_7},\,{a_8}} \right)\).

Số cách chọn 5 chữ số còn lại: \(A_7^5\) cách.

\( \Rightarrow \) Có \(7.A_7^5\) số.

\( \Rightarrow n\left( M \right) = 2.7.A_7^5 + 8.A_7^5 = 55440\).

Vậy xác suất của biến cố M là \(P\left( M \right) = \dfrac{{n\left( M \right)}}{{n\left( \Omega  \right)}} = \dfrac{{55440}}{{9.A_9^7}} = \dfrac{{11}}{{324}}\) 

Chọn C.

Phương pháp giải:

- Gọi số tự nhiên có 4 chữ số khác nhau là \(\overline {abcd} \,\,\left( {a \ne 0,\,\,a \ne b \ne c \ne d} \right)\). Chọn lần lượt từng chữ số, áp dụng quy tắc nhân tính số phần tử của tập hợp \(S\).

- Chọn ngẫu nhiên 2 số từ \(S\) \( \Rightarrow \) Không gian mẫu.

- Tính số các số chẵn và số các số lẻ trong tập hợp \(S\).

- Gọi A là biến cố: “tổng hai số lấy được là một số chẵn” \( \Rightarrow \) Cả hai số lấy được hoặc cùng chẵn, hoặc cùng lẻ. Tính số phần tử của biến cố A.

- Tính xác suất của biến cố A là: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Gọi số tự nhiên có 4 chữ số khác nhau là \(\overline {abcd} \,\,\left( {a \ne 0,\,\,a \ne b \ne c \ne d} \right)\).

- Số cách chọn \(a\): 6 cách.

- Số cách chọn \(b,c,d\): \(A_6^3\) cách.

\( \Rightarrow \) Có \(6.A_6^3 = 720\) số tự nhiên có 4 chữ số khác nhau được lập từ các chữ số 0, 1, 2, 3, 4, 5, 6.

\( \Rightarrow \) Tập hợp \(S\) có 720 phần tử.

Chọn ngẫu nhiên 2 số từ \(S\) \( \Rightarrow \) Không gian mẫu: \(n\left( \Omega  \right) = C_{720}^2\).

Trong các số \(0,1,2,3,4,5,6\) có 4 số chẵn và 3 số lẻ.

a. Tính số các số chẵn được lập từ 7 chữ số trên:

Nếu số đó có dạng \(\overline {abc0}  \Rightarrow \) có \(A_6^3 = 120\) số thỏa mãn.

Nếu số đó dạng \(\overline {abcd} ;\,\,\,d \in \left\{ {2;4;6} \right\} \Rightarrow \) có \(3.5.A_5^2 = 300\) số thỏa mãn.

Vậy có 420 số chẵn được tạo từ các số đã cho.

b. Tính số các số lẻ được lập từ 7 chữ số trên:

Số các số lẻ \( = 720 - 420 = 300\) số.

Gọi A là biến cố: “tổng hai số lấy được là một số chẵn” \( \Rightarrow \) Cả hai số lấy được hoặc cùng chẵn, hoặc cùng lẻ.

- Lấy hai số chẵn từ tập \(S\) có \(C_{420}^2\) cách.

- Lấy hai số lẻ từ tập \(S\) có \(C_{300}^2\) cách.

\( \Rightarrow n\left( A \right) = C_{420}^2 + C_{300}^2\).

Vậy xác suất của biến cố A là: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{C_{300}^2 + C_{420}^2}}{{C_{720}^2}}\).

Chọn C.

Phương pháp giải:

Xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\)

Lời giải chi tiết:

Số phần tử của không gian mẫu: \(n\left( \Omega  \right) = 6!\)

Để nhóm bất kì 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của ba lớp A, B, C thì dãy 6 học sinh là 2 bộ hoán vị trùng nhau của bộ 3 hs A, B, C

Ví dụ: ABC.ABC

Số phần tử của A là: \(n\left( A \right) = 3! = 6\)\( \Rightarrow P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{6}{{6!}} = \dfrac{1}{{120}}\).

Chọn A.

Phương pháp giải:

- Tính xác suất để người đó gieo súc sắc thắng.

- Tính xác suất để người đó thắng ít nhất hai ván.

Chi thành hai TH: thắng 2 ván và thắng 3 ván.

Lời giải chi tiết:

- Tính xác suất để người đó gieo súc sắc thắng trong 1 ván (nghĩa là gieo được ít nhất 2 mặt 6 chấm).

Số phần tử của không gian mẫu \(n\left( \Omega  \right) = {6^3} = 216\)

Gọi A là biến cố: “Gieo được ít nhất 2 mặt 6 chấm”

Số cách gieo được hai mặt 6 chấm là: \(C_3^2.1.1.5 = 15\) cách

Số cách gieo được ba mặt 6 chấm là: \(1\) cách

Số cách gieo được ít nhất 2 mặt 6 chấm là: \(n\left( A \right) = 15 + 1 = 16\) cách

Xác suất để người đó gieo thắng 1 ván là: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{16}}{{216}} = \dfrac{2}{{27}}\)

Do đó xác suất để thua 1 ván là \(1 - P\left( A \right) = 1 - \dfrac{2}{{27}} = \dfrac{{25}}{{27}}\)

- Tính xác suất để người đó thắng ít nhất 2 ván.

TH1: Thắng 2 ván, thua 1 ván

Xác suất để người đó thắng 2 ván thua 1 ván là \(C_3^2.\dfrac{2}{{27}}.\dfrac{2}{{27}}.\dfrac{{25}}{{27}} = \dfrac{{100}}{{6561}}\)

Xác suất để người đó thắng cả 3 ván là: \({\left( {\dfrac{2}{{27}}} \right)^3} = \dfrac{8}{{19683}}\)

Theo quy tắc cộng xác suất ta có: Xác suất để người đó thắng ít nhất 2 ván là:

\(P = \dfrac{{100}}{{6561}} + \dfrac{8}{{19683}} = \dfrac{{308}}{{19683}}\).

Chọn B.

Phương pháp giải:

- Tính số phần tử của không gian mẫu.

- Gọi A là biến cố: “chọn được khách hàng được tặng cả 3 món quà”. Để khách hàng nhận được cả ba món quà thì số thứ tự của khách hàng đó phải đồng thời chia hết cho 4, 5, 6. Tìm số các số thứ tự thỏa mãn điều kiện.

- Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Chọn ngẫu nhiên một khách trong 200 khách \( \Rightarrow n\left( \Omega  \right) = C_{200}^1 = 200\).

Gọi A là biến cố: “chọn được khách hàng được tặng cả 3 món quà”.

Để khách hàng nhận được cả ba món quà thì số thứ tự của khách hàng đó phải đồng thời chia hết cho 4, 5, 6.

Ta có BCNN(4;5;6) = 60.

Gọi \(x\) là số thứ tự của khách hàng được tặng cả 3 món quà \( \Rightarrow x\,\, \vdots \,\,60,\,\,x \in \left[ {2;100} \right],\,\,x \in \mathbb{N}\).

\( \Rightarrow x \in \left\{ {60;120;180} \right\}\) \( \Rightarrow n\left( A \right) = 3\).

Vậy \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{3}{{200}}\).

Chọn D.

Phương pháp giải:

- Tính số phần tử của không gian mẫu.

- Gọi A là biến cố: “tổng các số ghi trên 3 thẻ chia hết cho 3”.

Ta có các trường hợp sau:

   TH1: Cả 3 số chia hết cho 3 .

   TH2: Cả 3 số chia cho 3 dư 1 .

   TH3: Cả 3 số chia cho 3 dư 2 .

- Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Rút ngẫu nhiên 3 thẻ từ 50 tấm thẻ \( \Rightarrow n\left( \Omega  \right) = C_{50}^3\).

Gọi A là biến cố: “tổng các số ghi trên 3 thẻ chia hết cho 3”.

Ta chia 50 tấm thẻ thành 3 tập hợp:

\(\begin{array}{l}A = \left\{ {1;4;7;10;13;16;....;49} \right\}\,\,\,\left( {17pt} \right)\\B = \left\{ {2;5;8;11;14;17;...;50} \right\}\,\,\,\,\left( {17pt} \right)\\C = \left\{ {3;6;9;12;15;18;...;48} \right\}\,\,\,\left( {16pt} \right)\end{array}\)

Để tổng 3 số trên 3 tấm thẻ chia hết cho 3 ta có các trường hợp sau:

TH1: Cả 3 số chia hết cho 3 \( \Rightarrow \) Có \(C_{16}^3\) cách chọn.

TH2: Cả 3 số chia cho 3 dư 1 \( \Rightarrow \) Có \(C_{17}^3\) cách chọn.

TH3: Cả 3 số chia cho 3 dư 2 \( \Rightarrow \) Có \(C_{17}^3\) cách chọn.

TH4: 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2 \( \Rightarrow \) Có \(C_{16}^1.C_{17}^1.C_{17}^1\) cách chọn.

\( \Rightarrow n\left( A \right) = C_{16}^3 + C_{17}^3 + C_{17}^3 + C_{16}^1.C_{17}^1.C_{17}^1 = 6544\).

Vậy xác suất của biến cố A là: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{6544}}{{C_{50}^3}} = \dfrac{{409}}{{1225}}\).

Chọn D.

Phương pháp giải:

- Tính số phần tử của không gian mẫu.

- Gọi A là biến cố: “tích các số ghi trên 5 quả cầu đó chia hết cho 3”. Để tích 5 số chia hết cho 3 thì trong 5 số phải có ít nhất 1 số thuộc tập X. Xét biến cố đối.

- Sử dụng công thức \(P\left( A \right) = 1 - P\left( {\bar A} \right)\).

Lời giải chi tiết:

Chọn ngẫu nhiên 5 quả cầu từ 10 quả cầu \( \Rightarrow \) Không gian mẫu: \(n\left( \Omega  \right) = C_{10}^5\).

Gọi A là biến cố: “tích các số ghi trên 5 quả cầu đó chia hết cho 3”.

Ta chia các số từ 1 đến 10 thành 2 tập hợp: \(X = \left\{ {3;6;9} \right\}\) và \(Y = \left\{ {1;2;4;5;7;8;10} \right\}\).

Để tích 5 số chia hết cho 3 thì trong 5 số phải có ít nhất 1 số thuộc tập X.

Xét biến cố đối: “Không có số nào trong 5 số chia hết cho 3” \( \Rightarrow \) Chọn 5 số từ tập hợp Y có \(C_7^5\) cách.

\( \Rightarrow n\left( {\bar A} \right) = C_7^5\) \( \Rightarrow P\left( {\bar A} \right) = \dfrac{{C_7^5}}{{C_{10}^5}} = \dfrac{1}{{12}}\).

Vậy \(P\left( A \right) = 1 - P\left( {\bar A} \right) = \dfrac{{11}}{{12}}\).

Chọn D.

Phương pháp giải:

- Tính số phần tử của không gian mẫu.

- Gọi Gọi A là biến cố: “tích số ghi trên ba tấm thẻ là một số chẵn” \( \Rightarrow \) Biến cố đối: \(\bar A\): “tích số ghi trên ba tấm thẻ là một số lẻ”. Khi đó cả 3 tấm thẻ được chọn mang số lẻ, tính \(n\left( {\bar A} \right)\).

- Tính xác suất của biến cố: \(P\left( A \right) = 1 - P\left( {\bar A} \right) = 1 - \dfrac{{n\left( {\bar A} \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Không gian mẫu: \(n\left( \Omega  \right) = C_{12}^3 = 220\).

Gọi A là biến cố: “tích số ghi trên ba tấm thẻ là một số chẵn” \( \Rightarrow \) Biến cố đối: \(\bar A\): “tích số ghi trên ba tấm thẻ là một số lẻ”.

\( \Rightarrow \) Cả 3 tấm thẻ được chọn mang số lẻ \( \Rightarrow n\left( {\bar A} \right) = C_6^3 = 20\).

\( \Rightarrow P\left( {\bar A} \right) = \dfrac{{n\left( {\bar A} \right)}}{{n\left( \Omega  \right)}} = \dfrac{{20}}{{220}} = \dfrac{1}{{11}}\).

Vậy \(P\left( A \right) = 1 - P\left( {\bar A} \right) = 1 - \dfrac{1}{{11}} = \dfrac{{10}}{{11}}\).

Chọn C.

Phương pháp giải:

- Gọi số phần quà Sử - Địa là \(x\), số phần quà Sử - GDCD là \(y\) và số phần quà Địa – GDCD là \(z\), lập hệ phương trình giải tìm \(x,\,\,y,\,\,z\).

- Tính không gian mẫu.

- Gọi A là biến cố: “hai phần quà lấy được khác nhau”, tính số phần tử của biến cố A.

- Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Gọi số phần quà Sử - Địa là \(x\), số phần quà Sử - GDCD là \(y\) và số phần quà Địa – GDCD là \(z\) ta có:

\(\left\{ \begin{array}{l}x + y + z = 15\\x + y = 12\\y + z = 10\\x + z = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 7\\z = 3\end{array} \right.\)

Suy ra số phần qùa Sử - Địa là 5.

            Số phần quà Sử - GDCD là 7.

            Số phần quà Địa – GDCD là 3.

Chọn 2 trong 15 phần quà \( \Rightarrow \) Không gian mẫu \(n\left( \Omega  \right) = C_{15}^2 = 105\).

Gọi A là biến cố: “hai phần quà lấy được khác nhau”, khi đó ta có:

\(n\left( A \right) = C_5^1.C_7^1 + C_7^1.C_3^1 + C_3^1.C_5^1 = 71\).

Vậy \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{71}}{{105}}\).

Chọn A.

Phương pháp giải:

- Gọi số tự nhiên có 4 chữ số khác nhau là \(\overline {abcd} \,\,\left( {a \ne 0,\,\,a,b,c,d \in \mathbb{N},\,\,0 \le a,b,c,d \le 9} \right)\). Tính số phần tử của không gian mẫu.

- Gọi A là biến cố: “Số được chọn có các chữ số sắp xếp theo thứ tự tăng dần và không chứa hai chữ số nguyên nào liên tiếp nhau” \( \Rightarrow 1 \le a < b < c < d \le 9\).

- Từ yêu cầu bài toán, suy ra được điều kiện \(1 \le a < b - 1 < c - 2 < d - 3 \le 6\), chọn cặp các chữ số \(\left( {a;b - 1;c - 2;d - 3} \right)\) thỏa mãn điều kiện trên, từ đó tính được \(n\left( A \right)\).

- Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Gọi số tự nhiên có 4 chữ số khác nhau là \(\overline {abcd} \,\,\left( {a \ne 0,\,\,a,b,c,d \in \mathbb{N},\,\,0 \le a,b,c,d \le 9} \right)\).

- Số cách chọn \(a\): 9 cách \(\left( {a \ne 0} \right)\).

- Số cách chọn \(b,\,\,c,\,\,d\): \(A_9^3 = 504\) cách.

\( \Rightarrow \) Số phần tử của không gian mẫu là \(n\left( \Omega  \right) = 9.504 = 4536\).

Gọi A là biến cố: “Số được chọn có các chữ số sắp xếp theo thứ tự tăng dần và không chứa hai chữ số nguyên nào liên tiếp nhau”.

\( \Rightarrow 1 \le a < b < c < d \le 9\).

Vì các số \(a,\,\,b,\,\,c,\,\,d\) không có hai số nào là hai số nguyên liên tiếp nên ta có:

\(\left\{ \begin{array}{l}b > a + 1\\c > b + 1\\d > c + 1\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}a < b - 1\\b < c - 1 \Rightarrow b - 1 < c - 2\\c < d - 1 \Rightarrow c - 2 < d - 3\end{array} \right.\).

Khi đó ta có \(1 \le a < b - 1 < c - 2 < d - 3 \le 6\).

Số cách chọn được 1 bộ số \(\left( {a;b - 1;c - 2;d - 3} \right)\) là \(C_6^4 = 15\) cách. Ứng với mỗi cách chọn 1 bộ số \(\left( {a;b - 1;c - 2;d - 3} \right)\) ta được 1 bộ số \(\left( {a;b;c;d} \right)\) thỏa mãn yêu cầu bài toán \( \Rightarrow n\left( A \right) = 15\).

Vậy xác suất của biến cố A là \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{15}}{{4536}} = \dfrac{5}{{1512}}\).

Chọn D.

Phương pháp giải:

- Tính số phần tử của không gian mẫu.

- Gọi A là biến cố: “Học sinh lớp C ngồi giữa 2 học sinh lớp B”.

   + Xếp cố định 1 học sinh lớp C.

   + Xếp 2 học sinh lớp B.

   + Xếp 3 học sinh còn lại.

- Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Xếp 6 học sinh quanh một bàn tròn \( \Rightarrow n\left( \Omega  \right) = 5! = 120\).

Gọi A là biến cố: “Học sinh lớp C ngồi giữa 2 học sinh lớp B”.

Cố định học sinh lớp C, xếp 2 học sinh lớp B ngồi hai bên học sinh lớp C có \(2! = 2\) cách.

Xếp 3 học sinh lớp A vào 3 ghế còn lại có \(3! = 6\) cách.

\( \Rightarrow n\left( A \right) = 2.6 = 12\).

Vậy xác suất của biến cố A là: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{12}}{{120}} = \dfrac{1}{{10}}\).

Chọn B.

Phương pháp giải:

- Dựa vào phương trình để tìm điêu kiện của \(a;b.\)

- Tính xác suất của bài toán.

Lời giải chi tiết:

Ta có \({x^2} + ax + b = 0\) có nghiệm khi \(\Delta  = {a^2} - 4b \ge 0 \Leftrightarrow {a^2} \ge 4b\).

Mà \(1 \le a;\,\,\,b \le 6\) nên ta xét các trường hợp sau:

\( + )\,\,\,b = 1 \Rightarrow a \in \left\{ {2;3;4;5;6} \right\} \Rightarrow \) có 5 cặp số thỏa mãn.

\( + )\,\,\,b = 2 \Rightarrow a \in \left\{ {3;4;5;6} \right\} \Rightarrow \) có 4 cặp thỏa mãn.

\( + )\,\,\,b = 3 \Rightarrow a \in \left\{ {4;5;6} \right\} \Rightarrow \) có 3 cặp thỏa mãn.

\( + )\,\,\,b = 4 \Rightarrow a \in \left\{ {4;5;6} \right\} \Rightarrow \) có 3 cặp thỏa mãn.

\( + )\,\,\,\,b = 5 \Rightarrow a \in \left\{ {5;6} \right\} \Rightarrow \) có 2 cặp thỏa mãn.

\( + )\,\,\,b = 6 \Rightarrow a \in \left\{ {5;6} \right\} \Rightarrow \) có 2 cặp thỏa mãn.

Vậy tổng có 19 cặp thỏa mãn\( \Rightarrow n\left( A \right) = 19\). Mà không gian mẫu là \({6^2} = 36\).

Vậy xác suất của bài toán là \(P = \frac{{19}}{{36}}\)

Chọn B.

Phương pháp giải:

- Tính số phần tử của không gian mẫu.

- Gọi A là biến cố: “Số được chọn có đúng 2 chữ số chẵn”, số phần tử của A bằng Số các số có 4 chữ số khác nhau trong đó có 2 chữ số chẵn, hai chữ số lẻ là \({\left( {C_4^2} \right)^2}.4!\) (bao gồm cả số có chữ số 0 đứng đầu) - Số các số có 4 chữ số khác nhau trong đó có 2 chữ số chẵn, hai chữ số lẻ trong đó bắt buộc chữ số 0 đứng đầu.

- Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Gọi số tự nhiên có 4 chữ số là \(\overline {abcd} \,\,\,\left( {a \ne 0} \right)\).

Không gian mẫu: \(n\left( \Omega  \right) = 7.A_7^3 = 1470\).

Gọi A là biến cố: “Số được chọn có đúng 2 chữ số chẵn”.

Chọn 2 chữ số chẵn trong các số 0, 1, 2, 3, 4, 5, 6, 7 có \(C_4^2\) cách, chọn 2 chữ số lẻ trong các số 0, 1, 2, 3, 4, 5, 6, 7 có \(C_4^2\) cách.

\( \Rightarrow \) Số các số có 4 chữ số khác nhau trong đó có 2 chữ số chẵn, hai chữ số lẻ là \({\left( {C_4^2} \right)^2}.4!\) (bao gồm cả số có chữ số 0 đứng đầu).

Số các số có 4 chữ số khác nhau trong đó có 2 chữ số chẵn, hai chữ số lẻ trong đó bắt buộc chữ số 0 đứng đầu là: \(C_3^1.C_4^2.3!\).

\( \Rightarrow n\left( A \right) = {\left( {C_4^2} \right)^2}.4! - C_3^1.C_4^2.3! = 756\).

Vậy \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{756}}{{1470}} = \dfrac{{18}}{{35}}\).

Chọn D.

Phương pháp giải:

- Tìm số cách để sắp xếp Kỷ và Hợi.

- Tìm số cách sắp xếp 34 bạn còn lại.

- Áp dụng quy tắc nhân rồi tính xác suất.

Lời giải chi tiết:

Xếp 36 em học sinh vào 36 ghế \( \Rightarrow \) Không gian mẫu \(n\left( \Omega  \right) = 36!\).

Gọi A là biến cố: “Hai em Kỷ và Hợi ngồi cạnh nhau theo một hàng ngang hoặc một hàng dọc”.

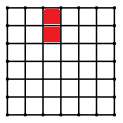
Chọn 1 hàng hoặc cột để xếp Kỷ và Hợi có 12 cách.

Trên mỗi hàng hoặc cột xếp 2 em Kỷ và Hợi gần nhau có \(5.2 = 10\) cách.

Sắp xếp 34 bạn còn lại có 34! cách.

\( \Rightarrow n\left( A \right) = 12.10.34!\).

Vậy xác suất của biến cố A là: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{12.10.34!}}{{36!}} = \dfrac{2}{{21}}\).

Chọn D.

Phương pháp giải:

- Tính số phần tử của không gian mẫu: Chọn mỗi tổ 3 người, sau đó chọn 1 người làm đội trưởng.

- Gọi A là biến cố: “ba tổ trường đều là ba bác sĩ”. Tính số phần tử của biến cố A.

- Tính xác suất của biến cố A.

Lời giải chi tiết:

+ Tính số phần tử của không gian mẫu:

Chọn 3 người cho tổ 1 có \(C_9^3\) cách. Chọn 1 người làm tổ trưởng có 3 cách.

Chọn 3 người cho tổ 2 có \(C_6^3\) cách. Chọn 1 người làm tổ trưởng có 3 cách.

Chọn 3 người cho tổ 3 có \(C_3^3\) cách. Chọn 1 người làm tổ trưởng có 3 cách.

\( \Rightarrow n\left( \Omega  \right) = C_9^3.C_6^3.C_3^3{.3^3} = 45360\).

+ Gọi A là biến cố: “ba tổ trường đều là ba bác sĩ”, tức là mỗi tổ có ít nhất 1 bác sĩ.

TH1: Tổ 1 có 2 bác sĩ, chọn 1 bác sĩ làm tổ trưởng, 2 tổ còn lại mỗi tổ có 1 bác sĩ.

\( \Rightarrow \) Có \(C_4^2.C_2^1.C_5^1.C_2^1.C_4^2 = 720\) cách.

TH2: Tổ 2 có 2 bác sĩ, chọn 1 bác sĩ làm tổ trưởng, 2 tổ còn lại mỗi tổ có 1 bác sĩ.

Tương tự TH1, có \(720\) cách.

TH3: Tổ 3 có 2 bác sĩ, chọn 1 bác sĩ làm tổ trưởng, 2 tổ còn lại mỗi tổ có 1 bác sĩ.

Tương tự TH1, có \(720\) cách.

\( \Rightarrow n\left( A \right) = 720.3 = 2160\).

Vậy \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{2160}}{{45360}} = \dfrac{1}{{21}}\).

Chọn B.

Phương pháp giải:

Xác suất của biến cố A là: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Gọi số đó là: \(\overline {8{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \).

Số phần tử của không gian mẫu: \(n\left( \Omega  \right) = {10^6}\)

Giả sử, biến cố A: ‘Số điện thoại này là may mắn”

Trong các số đó, số các số mà bốn chữ số đầu là chữ số chẵn phân biệt và ba chữ số còn lại là lẻ là: \(A_4^3{.5^3}\) (số)

Trong các số đó, số các số mà bốn chữ số đầu là chữ số chẵn phân biệt và ba chữ số còn lại là lẻ, đồng thời, số 0 và 9 đứng liền nhau (tức là : \({a_3} = 0,\,\,{a_4} = 9\))  là: \(A_3^2{.5^2}\) (số)

\( \Rightarrow n\left( A \right) = A_4^3{.5^3} - A_3^2{.5^2}\)\( \Rightarrow P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{2850}}{{{{10}^6}}} = \dfrac{{285}}{{{{10}^5}}}\).

Chọn D.

Phương pháp giải:

- Tính số phần tử của không gian mẫu, sử dụng hoán vị.

- Gọi X là biến cố: “hai bạn A và B không ngồi cạnh nhau”, xác định biến cố đối \(\bar X\).

- Tính số phần tử của biến cố đối \(\bar X\).

- Tính xác suất của biến cố đối \(\bar X\).

- Tính xác suất của biến cố X: \(P\left( X \right) = 1 - P\left( {\bar X} \right)\).

Lời giải chi tiết:

Xếp 5 học sinh A, B, C, D, E vào một dãy 5 ghế thẳng hàng có \(5!\) cách xếp \( \Rightarrow n\left( \Omega  \right) = 5! = 120\).

Gọi X là biến cố: “hai bạn A và B không ngồi cạnh nhau” \( \Rightarrow \) Biến cố đối \(\bar X\): “hai bạn A và B ngồi cạnh nhau”.

Buộc hai bạn A và B coi là 1 phần tử, có 2! cách đổi chỗ 2 bạn A và B trong buộc này.

Bài toán trở thành xếp 4 bạn (AB), C, D, E vào một dãy 4 ghế thẳng hàng \( \Rightarrow \) Có 4! cách xếp.

\( \Rightarrow n\left( {\bar X} \right) = 2!.4! = 48\).

\( \Rightarrow P\left( {\bar X} \right) = \dfrac{{n\left( {\bar X} \right)}}{{n\left( \Omega  \right)}} = \dfrac{{48}}{{120}} = \dfrac{2}{5}\).

Vậy \(P\left( X \right) = 1 - P\left( {\bar X} \right) = 1 - \dfrac{2}{5} = \dfrac{3}{5}\).

Chọn B.

Phương pháp giải:

Sử dụng nguyên tắc vách ngăn: Xếp 4 bạn nam trước, tạo thành 5 vách ngăn, sau đó xếp 2 bạn nữ vào 2 trong 5 vách ngăn đó.

Lời giải chi tiết:

Xếp 4 bạn nam và 2 bạn nữ thành một hàng ngang \( \Rightarrow n\left( \Omega  \right) = 6! = 720\).

Gọi A là biến cố: “2 bạn nữ không ngồi cạnh nhau”.

Xếp 4 bạn nam có 4! cách, khi đó sẽ tạo ra 5 khoảng trống giữa 4 bạn nam, xếp 2 bạn nữ vào 2 trong 5 khoảng trống này có \(A_5^2\) cách.

\( \Rightarrow n\left( A \right) = 4!.A_5^2 = 480\).

Vậy \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{480}}{{720}} = \dfrac{2}{3}\).

Chọn D.

Phương pháp giải:

- Gọi \({A_1}\) là biến cố máy thứ nhất hoạt động tốt, \({A_2}\) là biến cố máy thứ hai hoạt động tốt.

- Dựa vào giả thiết xác định \(P\left( {{A_1}} \right),\,\,P\left( {\overline {{A_1}} } \right)\), \(P\left( {{A_2}} \right),\,\,P\left( {\overline {{A_2}} } \right)\).

- Xác suất để công ty hoàn thành đơn hàng đúng hạn là: \(P = P\left( {{A_1}} \right).P\left( {\overline {{A_2}} } \right) + P\left( {{A_2}} \right).P\left( {\overline {{A_1}} } \right) + P\left( {{A_1}} \right).P\left( {{A_2}} \right)\).

Lời giải chi tiết:

Gọi \({A_1}\) là biến cố máy thứ nhất hoạt động tốt, \({A_2}\) là biến cố máy thứ hai hoạt động tốt.

Ta có: \(\left\{ \begin{array}{l}P\left( {{A_1}} \right) = 90\% ,\,\,P\left( {\overline {{A_1}} } \right) = 10\% \\P\left( {{A_2}} \right) = 85\% ,\,\,P\left( {\overline {{A_2}} } \right) = 15\% \end{array} \right.\).

Vậy xác suất để công ty hoàn thành đơn hàng đúng hạn là:

\(\begin{array}{l}P = P\left( {{A_1}} \right).P\left( {\overline {{A_2}} } \right) + P\left( {{A_2}} \right).P\left( {\overline {{A_1}} } \right) + P\left( {{A_1}} \right).P\left( {{A_2}} \right)\\\,\,\,\,\, = 90\% .15\%  + 85\% .10\%  + 90\% .85\% \\\,\,\,\,\, = 98,5\% \end{array}\)

Chọn C.

Phương pháp giải:

- Đường thẳng đi qua \(M,\,\,N\) nhận \(\overrightarrow {MN} \) là 1 VTCP.

- Mọi vectơ cùng phương với \(\overrightarrow {MN} \) đều là VTCP của đường thẳng \(d\).

Lời giải chi tiết:

Gọi số có 3 chữ số là \(\overline {abc} \,\,\left( {a,\,\,b,\,\,c \in \mathbb{N},\,\,0 \le a,\,b,\,\,c \le 9,\,\,a \ne 0} \right)\) \(\left( {a \ne b \ne c} \right)\).

Số cách chọn \(a\) là 9 cách \(\left( {a \ne 0} \right)\).

Số cách chọn \(b\) là 9 cách.

Số cách chọn \(c\) là 8 cách.

\( \Rightarrow \) Không gian mẫu \(n\left( \Omega  \right) = 9.9.8 = 648\).

Gọi A là biến cố: “Số được chọn có tổng các chữ số là chẵn”.

\( \Rightarrow a + b + c\) là số chẵn, khi đó ta có các trường hợp sau:

TH1: \(a,\,\,b,\,\,c\) đều là các số chẵn.

Chọn \(a\) có 4 cách chọn \(\left( {a \in \left\{ {2;4;6;8} \right\}} \right)\).

Chọn \(b\) có 4 cách chọn \(\left( {b \in \left\{ {0;2;4;6;8} \right\},\,\,b \ne a} \right)\),

Chọn \(c\) có 3 cách chọn \(\left( {c \in \left\{ {0;2;4;6;8} \right\},\,\,c \ne a,\,\,c \ne b} \right)\).

\( \Rightarrow \) Có \(4.4.3 = 48\) số.

TH2: \(a\) chẵn, \(b,\,\,c\) lẻ.

Chọn \(a\) có 4 cách chọn \(\left( {a \in \left\{ {2;4;6;8} \right\}} \right)\).

Chọn \(b\) có 5 cách chọn \(\left( {b \in \left\{ {1;3;5;7;9} \right\}} \right)\),

Chọn \(c\) có 4 cách chọn \(\left( {c \in \left\{ {1;3;5;7;9} \right\},\,\,c \ne b} \right)\).

\( \Rightarrow \) Có \(4.5.4 = 80\) số.

TH3: \(b\) chẵn, \(a,\,\,c\) lẻ.

Chọn \(a\) có 5 cách chọn \(\left( {a \in \left\{ {1;3;5;7;9} \right\}} \right)\).

Chọn \(b\) có 5 cách chọn \(\left( {b \in \left\{ {0;2;4;6;8} \right\}} \right)\),

Chọn \(c\) có 4 cách chọn \(\left( {c \in \left\{ {1;3;5;7;9} \right\},\,\,c \ne a} \right)\).

\( \Rightarrow \) Có \(5.5.4 = 100\) số.

TH4: \(c\) chẵn, \(a,\,\,b\) lẻ.

Chọn \(a\) có 5 cách chọn \(\left( {a \in \left\{ {1;3;5;7;9} \right\}} \right)\).

Chọn \(b\) có 4 cách chọn \(\left( {b \in \left\{ {1;3;5;7;9} \right\},\,\,b \ne a} \right)\),

Chọn \(c\) có 5 cách chọn \(\left( {c \in \left\{ {0;2;4;6;8} \right\}} \right)\).

\( \Rightarrow \) Có \(5.5.4 = 100\) số.

\( \Rightarrow n\left( A \right) = 48 + 80 + 100 + 100 = 328\).

Vậy xác suất của biến cố A là \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{328}}{{648}} = \dfrac{{41}}{{81}}\).

Chọn A.

Phương pháp giải:

- Gọi số có 3 chữ số là \(\overline {abc} \,\,\left( {0 \le a,\,\,b,\,\,c \le 9,\,\,a \ne 0,\,\,a,\,\,b,\,\,c \in \mathbb{N}} \right)\). Tính số phần tử của không gian mẫu.

- Gọi A là biến cố: “số chọn được có tổng các chữ số hàng trăm và hàng đơn vị bằng hai lần chữ số hàng chục”. Suy ra \(a + c = 2b\) \( \Rightarrow \) \(a,\,\,c\) cùng tính chẵn lẻ.

- Chia các TH: TH1: \(\left\{ {a;c} \right\} \in \left\{ {1;3;5;7;9} \right\}\) và TH2: \(\left\{ {a;c} \right\} \in \left\{ {0;2;4;6;8} \right\}\).

- Tính số phần tử của biến cố A.

- Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải chi tiết:

Gọi số có 3 chữ số là \(\overline {abc} \,\,\left( {0 \le a,\,\,b,\,\,c \le 9,\,\,a \ne 0,\,\,a,\,\,b,\,\,c \in \mathbb{N}} \right)\).

Số cách chọn \(a\) là: 9 cách \(\left( {a \ne 0} \right)\).

Số cách chọn \(b\) là 9 cách \(\left( {b \ne a} \right)\).

Số cách chọn \(c\) là: 8 cách \(\left( {c \ne a,\,\,b} \right)\).

Không gian mẫu: \(n\left( \Omega  \right) = 9.9.8 = 648\).

Gọi A là biến cố: “số chọn được có tổng các chữ số hàng trăm và hàng đơn vị bằng hai lần chữ số hàng chục”.

Ta có: \(a + c = 2b\) \( \Rightarrow a + c\) là số chẵn, \(a + c > 0\), do đó \(a,\,\,c\) cùng tính chẵn lẻ.

TH1: \(\left\{ {a;c} \right\} \in \left\{ {1;3;5;7;9} \right\}\).

- Số cách chọn \(a,\,\,c\) là \(A_5^2 = 20\) cách.

- Ứng với mỗi cách chọn \(a,\,\,c\) có duy nhất 1 cách chọn \(b\).

\( \Rightarrow \) TH1 có \(20\) số thỏa mãn.

TH2: \(\left\{ {a;c} \right\} \in \left\{ {0;2;4;6;8} \right\}\).

- Số cách chọn \(a,\,\,c\) là \(A_5^2 - 4 = 16\) cách (Trừ 4 bộ số mà \(a = 0\)).

- Ứng với mỗi cách chọn \(a,\,\,c\) có duy nhất 1 cách chọn \(b\).

\( \Rightarrow \) TH2 có \(16\) số thỏa mãn.

\( \Rightarrow n\left( A \right) = 20 + 16 = 36\).

Vậy \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{36}}{{648}} = \dfrac{1}{{18}}\).

Chọn B.

Lời giải chi tiết:

Gọi số tự nhiên có ba chữ số đôi một khác nhau là \(\overline {abc} \,\,\left( {0 \le a,\,\,b,\,\,c \le 9,\,\,a,\,\,b,\,\,c \in \mathbb{N},\,\,a \ne 0} \right)\).

Số cách chọn \(a\) là 9 cách \(\left( {a \ne 0} \right)\).

Số cách chọn \(b\) là 9 cách \(\left( {b \ne a} \right)\).

Số cách chọn \(c\) là 8 cách \(\left( {c \ne a,\,\,b} \right)\).

\( \Rightarrow n\left( \Omega  \right) = 9.9.8 = 648\).

Gọi A là biến cố: “số được chọn có tích các chữ số là số dương và chia hết cho 6.”

Ta có \(abc > 0,\,\,abc\,\, \vdots \,\,6 \Rightarrow \left\{ \begin{array}{l}abc\,\, \vdots \,\,2\\abc\,\, \vdots \,\,3\end{array} \right.\).

+ Vì \(abc\,\, \vdots \,\,2\) thì ít nhất một trong các số \(a,\,\,b,\,\,c\) thuộc \(\left\{ {2;4;6;8} \right\}\).

+ Vì \(abc\,\, \vdots \,\,3\) thì ít nhất một trong các số \(a,\,\,b,\,\,c\) thuộc \(\left\{ {3;6;9} \right\}\).

Khi đó ta có các trường hợp sau:

+ TH1: \(\overline {abc} \) có mặt chữ số 6, suy ra có \(3.A_8^2 = 168\) (số).

+ TH2: \(\overline {abc} \) có mặt chữ số 3 hoặc 9, không có mặt chữ số 6 và có ít nhất một trong các số \(a,\,\,b,\,\,c\) thuộc \(\left\{ {2;4;8} \right\}\), có \(2.\left( {C_3^1.C_3^1.3! + C_3^2.3!} \right) + C_3^1.3! = 162\) (số).

\( \Rightarrow n\left( A \right) = 168 + 162 = 330\) (số).

Vậy \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{330}}{{6498}} = \dfrac{{55}}{{108}}\).

Chọn A.

Phương pháp giải:

- Tính số phần tử của không gian mẫu.

- Tính số phần tử của biến cố. Số chia hết cho 3 là số có tổng các chữ số chia hết cho 3.

- Tính xác suất.

Lời giải chi tiết:

Ta có: \(n\left( \Omega  \right) = 9.9.8 = 648\).

Gọi \(N = \overline {abc} \) (với a, b, c \( \in \left\{ {0;1;2;3;4;5;6;7;8;9} \right\}\), a, b, c đôi một khác nhau, \(a \ne 0\) và \(a + b + c\) là số chia hết cho 3).

Gọi \(A = \left\{ {0;3;6;9} \right\},\,\,B = \left\{ {1;4;7} \right\};\,\,C = \left\{ {2;5;8} \right\}\).

Để \(a + b + c\) chia hết cho 3 ta có các trường hợp sau:

+ TH1: a, b, c thuộc A hoặc thuộc B hoặc thuộc C, có \(3.A_3^2 + 3! = 30\) (số).

+ TH2: 3 số a, b, c thuộc 3 tập khác nhau A, B, C, có \(2.C_3^1.C_3^1.2! + C_3^1.C_3^1.C_3^1.3! = 198\) (số).

Vậy có tất cả: 30 + 198 = 228 (số).

Vậy xác suất cần tìm là: \(P = \dfrac{{228}}{{648}} = \dfrac{{19}}{{54}}\).

Chọn C.

Phương pháp giải:

Sử dụng biến cố đối: Gọi \(A\) là biến cố: “Ba số được chọn không có 2 số nào là hai số nguyên liên tiếp” \( \Rightarrow \overline A \): “Ba số được chọn có 2 số nguyên liên tiếp”.

Lời giải chi tiết:

Số cách chọn ra ngẫu nhiên 3 số là \(C_{10}^3 \Rightarrow n\left( \Omega  \right) = C_{10}^3 = 120.\)

Gọi \(A\) là biến cố: “Ba số được chọn không có 2 số nào là hai số nguyên liên tiếp” \( \Rightarrow \overline A \): “Ba số được chọn có 2 số nguyên liên tiếp”.

TH1: 3 số chọn ra là 3 số tự nhiên liên tiếp: 8 cách.

TH2: 3 số chọn ra có 2 số tự nhiên liên tiếp.

+ 3 số chọn ra có cặp \(\left( {1;2} \right)\) hoặc \(\left( {9;10} \right)\) có: \(2.7 = 14\) cách.

+ 3 số chọn ra có cặp \(\left\{ {\left( {2;3} \right);\left( {3;4} \right);...;\left( {8;9} \right)} \right\}\) có \(7.6 = 42\) cách.

\( \Rightarrow n\left( A \right) = 120 - 8 - 14 - 42 = 56\).

Vậy \(P\left( A \right) = \dfrac{{56}}{{120}} = \dfrac{7}{{15}}\).  

Chọn C.

Lời giải chi tiết:

Chọn C.

Phương pháp giải:

- Liệt kê và tính xác suất của mỗi trường hợp mà có 2 người trùng đích.

- Sử dụng quy tắc cộng xác suất suy ra đáp án.

Lời giải chi tiết:

Xác suất để người thứ nhất, thứ hai, thứ ba bán trúng đích lần lượt là: \(P\left( {{A_1}} \right) = 0,8\); \(P\left( {{A_2}} \right) = 0,6\) ; \(P\left( {{A_3}} \right) = 0,5.\)

Xác suất để có đúng hai người bán trúng đích bằng:

\(\begin{array}{l}\,\,\,\,P\left( {{A_1}} \right).P\left( {{A_2}} \right).\overline {P\left( {{A_3}} \right)}  + P\left( {{A_1}} \right).\overline {P\left( {{A_2}} \right)} .P\left( {{A_3}} \right) + \overline {P\left( {{A_1}} \right)} .P\left( {{A_2}} \right).P\left( {{A_3}} \right)\\ = 0,8.0,6.0,5 + 0,8.0,4.0,5 + 0.2.0,6.0,5\\ = 0,46.\end{array}\)

Chọn C.

Phương pháp giải:

Sử dụng các công thức tính xác suất.

Lời giải chi tiết:

Gọi A là biến cố “người bắn súng bắn trúng đích”. Ta có \(P\left( A \right) = 0,6\)

Suy ra \(\bar A\)  là  biến cố “người bắn súng không bắn trúng đích”. Ta có \(P\left( {\bar A} \right) = 1 - P\left( A \right) = 1 - 0,6 = 0,4.\)

Xét phép thử “bắn ba lần độc lập” với biến cố “người đó bắn trúng đích đúng một lần”, ta có các biến cố xung khắc sau:

\(P\left( C \right) = 0,4.0,6.0,4 = 0,096.\)

\(P\left( D \right) = 0,4.0,4.0,6 = 0,096.\)

Xác suất để người đó bắn trúng đích đúng một lần là:

\(P = P\left( A \right) + P\left( B \right) + P\left( C \right) = 0,096 + 0,096 + 0,096 = 0,288.\)

Chọn D.

Phương pháp giải:

- Tính số phần tử của không gian mẫu.

- Gọi biến cố A : "Tích của hai số ghi trên thẻ là số chẵn" \( \Rightarrow \overline A \) : " Tích của hai số ghi trên thẻ là số lẻ".

- Tích của hai số ghi trên thẻ là số lẻ khi và chỉ khi cả 2 số đều là số lẻ.

- Tính số cách chọn 2 số lẻ từ các số từ 1 đến 19.

- Tính xác suất của biến cố \(\overline A \) : \(P\left( {\overline A } \right) = \dfrac{{n\left( {\overline A } \right)}}{{n\left( \Omega  \right)}}\)

- Tính xác suất của biến cố \(A\) : \(P\left( A \right) = 1 - P\left( {\overline A } \right)\).

Lời giải chi tiết:

Số phần tử của không gian mẫu : \(n\left( \Omega  \right) = C_{19}^2.\)

Giả sử biến cố A: ‘Tích của hai số ghi trên hai thẻ là một số chẵn’

\( \Rightarrow \overline A \) : ‘Tích của hai số ghi trên hai thẻ là một số lẻ’ (tức là cả hai số đều lẻ).

Từ 1 đến 19 có \(\left( {19 - 1} \right):2 + 1 = 10\) số lẻ.

Số cách chọn 2 số lẻ từ 10 số lẻ trên là \(C_{10}^2\) \( \Rightarrow {n_{\overline A }} = C_{10}^2.\)

\(\begin{array}{l} \Rightarrow P\left( {\overline A } \right) = \dfrac{{C_{10}^2}}{{C_{19}^2}} = \dfrac{5}{{19}}\\ \Rightarrow P\left( A \right) = 1 - \dfrac{5}{{19}} = \dfrac{{14}}{{19}}.\end{array}\)

Chọn B.

Phương pháp giải:

Tìm số phần tử của không gian mẫu.

Tính số các cách xếp các chữ số thỏa mãn yêu cầu bài toán và tính xác suất cần tìm.

Lời giải chi tiết:

Lập số tự nhiên có 6 chữ số từ các chữ số thuộc tập \(A\) nên số phần tử của không gian mẫu là:\(\left| \Omega  \right| = {6^6} = 46656\) (phần tử).

Gọi \(X\) là biến cố: “ Lấy ra ngẫu nhiên một số có 6 chữ số lập được sao cho số đó luôn xuất hiện 3 chữ số 2, các chữ số còn lại đôi một khác nhau”. Ta sẽ tìm số phần tử có lợi cho biến cố \(X\).

      Xếp 3 chữ số 2 vào 3 trong 6 vị trí bất kì có \(C_6^3\) cách xếp.

      Lấy ra 3 trong 5 số còn lại của tập \(A\) xếp vào 3 vị trí còn lại của số có 6 chữ số ta có \(C_5^3.3!\) cách xếp

Do đó, số phần tử có lợi cho biến cố \(X\) là \(C_6^3.C_5^3.3! = 1200\)

Vậy xác suất cần tìm là:\({P_X} = \dfrac{{1200}}{{\left| \Omega  \right|}} = \dfrac{{25}}{{972}}\)

Chọn A.

Phương pháp giải:

Sử dụng phương pháp tính xác suất của biến cố đối:

- Tính xác suất để không có viên bi nào trúng vòng 10.

- Từ đó suy ra kết quả của bài toán.

Lời giải chi tiết:

Gọi A là biến cố: “Có ít nhất một viên trúng vòng 10”.

Khi đó biến cố đối của biến cố A là: \(\overline A \): “Không có viên nào trúng vòng 10”.

\( \Rightarrow P\left( {\overline A } \right) = \left( {1 - 0,75} \right).\left( {1 - 0,85} \right) = 0,0375\).

\( \Rightarrow P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - 0,0375 = 0,9625\).

Chọn A.

Phương pháp giải:

Sử dụng các công thức tính xác suất.

·        Nếu A và B là hai biến cố độc lập thì \(P(AB) = P(A).P(B)\) .

·        Nếu A và B là hai biến cố xung khắc thì \(P(A \cup B) = P(A) + P(B)\) .

Nếu A và B là hai biến cố đối nhau thì \(P\left( A \right) + P(B) = 1\)

Lời giải chi tiết:

Gọi A là biến cố “chiếc tàu khoan trúng túi dầu”. Ta có \(P\left( A \right) = 0,4\)

Suy ra \(\bar A\)  là  biến cố “chiếc tàu khoan không trúng túi dầu”. Ta có \(P(\bar A) = 0,6\)

Xét phép thử “tàu khoan 5 lần độc lập” với biến cố

B:“chiếc tàu không khoan trúng túi dầu lần nào”, ta có \(P(B) = 0,{6^5} = 0,07776\)

Khi đó ta có \(\bar B\) “chiếc tàu khoan trúng túi dầu ít nhất một lần”. Ta có

\(P\left( {\bar B} \right) = 1 - P(B) = 1 - 0,07776 = 0,92224\)

Chọn D.

Phương pháp giải:

Ta tính xác suất người đó thắng 1 ván.

Sau đó tính xác suất người đó thắng ít nhất hai ván.

Lời giải chi tiết:

Xác suất xuất hiện mặt 6 chấm là \(\dfrac{1}{6}\), xác suất không xuất hiện mặt 6 chấm là \(\dfrac{5}{6}.\)

Người đó chơi thắng nếu xuất hiện ít nhất 2 mặt sáu chấm:

TH1: 2 mặt sáu chấm, 1 mặt không phải sáu chấm \( \Rightarrow \) Xác suất là: \({\left( {\dfrac{1}{6}} \right)^2}.\dfrac{5}{6}\).

TH2: 3 mặt sáu chấm \( \Rightarrow \) Xác suất là \({\left( {\dfrac{1}{6}} \right)^3}\).

\( \Rightarrow \) Xác suất để người đó thắng cuộc: \({\left( {\dfrac{1}{6}} \right)^2}.\dfrac{5}{6} + {\left( {\dfrac{1}{6}} \right)^3} = \dfrac{1}{{36}}\), suy ra xác suất thua 1 ván là \(\dfrac{{35}}{{36}}\).

Vậy xác suất để trong 3 ván, người đó thắng ít nhất hai ván là \({\left( {\dfrac{1}{{36}}} \right)^3} + C_3^2{\left( {\dfrac{1}{{36}}} \right)^2}.\dfrac{{35}}{{36}} = \dfrac{{53}}{{23328}}.\)

Chọn D.

Phương pháp giải:

Xác suất của biến cố A là: \(P(A) = \dfrac{{n(A)}}{{n(\Omega )}}\).

Lời giải chi tiết:

Số phần tử của không gian mẫu: \(n\left( \Omega  \right) = 9.9.8.7.6.5.4.3.2 = 648.7!\)

Gọi biến cố A: “chọn được một số có mặt bốn chữ số lẻ và chữ số 0 luôn đứng giữa hai chữ số lẻ”

- Chọn và sắp xếp 2 chữ số lẻ để đặt chữ số 0 vào giữa 2 chữ số đó, có: \(A_5^2\) (cách)

Coi bộ 2 chữ số lẻ đó và chữ số 0 là 1 bộ (3chữ số)

- Chọn 2 chữ số lẻ khác và 4 chữ số chẵn khác 0, có: \(C_3^2.1\) (cách)

Hoán vị 1 bộ (3 chữ số trên) và 6 chữ số vừa được chọn, có: \(7!\) (cách)

\( \Rightarrow n\left( A \right) = A_5^2.C_3^2.7!\)\( \Rightarrow P(A) = \dfrac{{n(A)}}{{n(\Omega )}} = \dfrac{{A_5^2.C_3^2.7!}}{{648.7!}} = \dfrac{5}{{54}}\).

Chọn A.

Lời giải chi tiết:

\( + )\) Gọi Số cách chọn ra 3 học sinh bất kỳ là không gian mẫu \( \Rightarrow {n_\Omega } = C_{40}^3 = 9880\)

\( + )\) Gọi A là biến cố chọn 3 cán bộ lớp mà không có cặp sinh đôi nào.

\( \Rightarrow \overline A \) là biến cố chọn 1 cặp sinh đôi.

\( + )\) Đầu tiên chọn 1 cặp sinh đôi trong 4 cặp sinh đôi

Thứ hai chọn 1 cặp sinh đôi còn lại từ 38 bạn

\( \Rightarrow \) Số cách chọn ra 1 cặp sinh đôi là:  \(C_4^1.C_{38}^1 = 152\)

\( \Rightarrow {P_{\overline A }} = \dfrac{{152}}{{9880}} = \dfrac{1}{{65}}\)

\( \Rightarrow {P_A} = 1 - {P_{\overline A }} = 1 - \dfrac{1}{{65}} = \dfrac{{64}}{{65}}\)

Chọn A.

Lời giải chi tiết:

Mỗi lớp cử ra 3 học sinh nên 10 lớp cử ra 30 học sinh

\( \Rightarrow \) Số lần bắt tay (bao gồm cả học sinh cùng lớp) bằng \(C_{30}^2\)

Mà số lần bắt tay của học sinh cùng lớp bằng \(10.C_3^2\)

\( \Rightarrow \) Số lần bắt tay nhau của các học sinh là: \(C_{30}^2 - 10.C_3^2 = 405\)

Chọn A.

Lời giải chi tiết:

3 đoạn thẳng với chiều dài a, b, c tạo thành 1 tam giác \( \Leftrightarrow \left\{ \begin{array}{l}a + b > c\\a + c > b\\b + c > a\end{array} \right.\)

Gọi: Số cách chọn 3 đoạn thẳng từ 5 đoạn thẳng là không gian mẫu\( \Rightarrow {n_\Omega } = C_5^3 = 10\)

Gọi: A là biến cố: “3 cạnh tạo thành 1 tam giác” \( \Rightarrow {n_A} = 3\left( {2;4;6/2;4;8/4;6;8} \right)\)

\( \Rightarrow {P_A} = \dfrac{3}{{10}}\) .

Chọn A.

Phương pháp giải:

Áp dụng công thức cộng và nhân xác suất.

Lời giải chi tiết:

Xác suất lấy được gói quà màu đỏ từ hộp I là: \(\dfrac{1}{6}.\dfrac{4}{{10}} = \dfrac{4}{{60}}\)

Xác suất lấy được gói quà màu đỏ từ hộp II là: \(\dfrac{5}{6}.\dfrac{2}{{10}} = \dfrac{{10}}{{60}}\)

\( \Rightarrow \)Xác suất để lấy được gói quà màu đỏ là: \(\dfrac{4}{{60}} + \dfrac{{10}}{{60}} = \dfrac{{14}}{{60}} = \dfrac{7}{{30}}\).

Chọn: B.

Lời giải chi tiết:

\( + )\) Số phần tử của không gian mẫu bốc ngẫu nhiêm 3 phiếu là: \(C_{50}^3\)

\( + )\) Gọi 4 cặp đó là: A; B; C; D, số phiếu không nằm trong 4 cặp trên là 45

Xét biến cố T trong 3 phiếu được chọn sẽ có 2 câu hỏi có cùng nội dung.

Số cách chọn ra 2 phiếu có cùng nội dung là: 4

Số cách chọn ra phiếu còn lại là: 48

\( \Rightarrow \) Số phần tử của T là: \(4.48\)

\( \Rightarrow {P_T} = \dfrac{{4.48}}{{C_{50}^3}}\)

\( \Rightarrow {P_{\overline T }} = 1 - \dfrac{{4.48}}{{C_{50}^3}} = \dfrac{{1213}}{{1225}}\)

Chọn D.

Lời giải chi tiết:

\( + )\) Số tự nhiên có 2 chữ số là: \(C_9^1.C_{10}^1 = 90\) số

\( + )\)\(\Omega \): “Chọn ngẫu nhiên 2 số từ tập hợp S” \( \Rightarrow {n_\Omega } = C_{90}^2\)

\( + )\) A: “Chọn được 2 số có chữ số hàng đơn vị giống nhau”.

\( \bullet \) TH1: Chữ số hàng đơn vị là 0 \( \Rightarrow \) Có 9 chữ số là: \(10;20;30;40;50;60;70;80;90\)

\( \Rightarrow \) Số cách chọn 2 số là: \(C_9^2\)

Tương tự với các số có chữ số hàng đơn vị là: \(1;2;3;4;5;6;7;8;9\)

\( \Rightarrow \) Có tất cả 10 trường hợp giống nhau.

\( \Rightarrow {n_A} = 10.C_9^2\)

\( \Rightarrow {P_A} = \dfrac{{10.C_9^2}}{{C_{90}^2}} = \dfrac{8}{{89}}\)

Chọn A.