30 bài tập khoảng cách vận dụng, vận dụng cao
Làm đề thiCâu hỏi 1 :
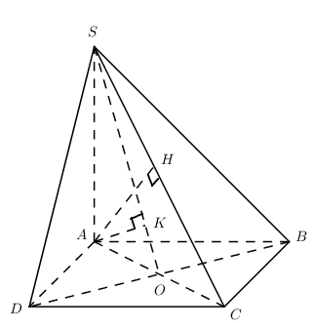
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\). Tam giác \(ABC\) đều, hình chiếu vuông góc \(H\) của đỉnh \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) trùng với trọng tâm của tam giác \(ABC\). Đường thẳng \(SD\) hợp với mặt phẳng \(\left( {ABCD} \right)\) góc \(30^\circ \). Tính khoảng cách \(d\) từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\) theo \(a\).
- A \(d = a\sqrt 3 .\)
- B \(d = a.\)
- C \(d = \dfrac{{a\sqrt {21} }}{7}.\)
- D \(d = \dfrac{{2a\sqrt {21} }}{{21}}.\)
Đáp án: C
Phương pháp giải:
- Xác định góc giữa cạnh bên \(SD\) và mặt đáy \(\left( {ABCD} \right)\) là góc giữa \(SD\) và hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\)
- Đổi khoảng cách từ \(d\left( {B;\left( {SCD} \right)} \right)\) sang \(d\left( {H;\left( {SCD} \right)} \right)\) với \(H\) là chân đường cao của khối chóp, sử dụng công thức: \(\dfrac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \dfrac{{BM}}{{HM}}\) với \(M = BH \cap \left( {SCD} \right)\).
- Xác định khoảng cách từ \(H\) đến \(\left( {SCD} \right)\). Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
Gọi \(H\) là trọng tâm tam giác đều \(ABC\) \( \Rightarrow SH \bot \left( {ABCD} \right)\).
\( \Rightarrow HD\) là hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\).
\( \Rightarrow \angle \left( {SD;\left( {ABCD} \right)} \right) = \angle \left( {SD;HD} \right) = \angle SDH = {30^0}\).
Ta có: \(\dfrac{{BH}}{{BO}} = \dfrac{2}{3} \Rightarrow \dfrac{{BH}}{{BD}} = \dfrac{1}{3} \Rightarrow \dfrac{{HD}}{{BD}} = \dfrac{2}{3}\).
Mà \(BH \cap \left( {SCD} \right) = D\)\( \Rightarrow \dfrac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \dfrac{{BD}}{{HD}} = \dfrac{3}{2}\)\( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = \dfrac{3}{2}d\left( {H;\left( {SCD} \right)} \right)\).
Ta có \(H\) là trọng tâm tam giác đều \(ABC\)nên \(HC \bot AB\). Mà \(AB\parallel CD\) nên \(HC \bot CD\).
Trong \(\left( {SHC} \right)\) kẻ \(HK \bot SC\).
Ta có \(\left\{ \begin{array}{l}CD \bot CH\\CD \bot SH\end{array} \right. \Rightarrow CD \bot \left( {SHC} \right)\) \( \Rightarrow CD \bot HK\).
\(\left\{ \begin{array}{l}HK \bot SC\\HK \bot CD\end{array} \right. \Rightarrow HK \bot \left( {SCD} \right)\) \( \Rightarrow d\left( {H;\left( {SCD} \right)} \right) = HK\).
Vì tam giác \(ABC\) đều cạnh \(a\) nên \(HC = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
Ta có: \(\dfrac{{HD}}{{BD}} = \dfrac{2}{3}\), mà \(BD = 2BO = 2.\dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \)\( \Rightarrow HD = \dfrac{2}{3}BD = \dfrac{{2a\sqrt 3 }}{3}\)
Xét tam giác vuông \(SHD\) ta có: \(SH = HD.\tan {30^0} = \dfrac{{2a\sqrt 3 }}{3}.\dfrac{{\sqrt 3 }}{3} = \dfrac{{2a}}{3}.\)
Áp dụng hệ thức lượng trong tam giác vuông \(SHC\) ta có: \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{C^2}}} = \dfrac{1}{{\dfrac{{4{a^2}}}{9}}} + \dfrac{1}{{\dfrac{{{a^2}}}{3}}} = \dfrac{{21}}{{4a^2}}.\)
\( \Rightarrow HK = \dfrac{{2\sqrt {21} }}{{21}}a\)
Vậy \(d\left( {B;\left( {SCD} \right)} \right) = \dfrac{3}{2}HK = \dfrac{{3\sqrt {21} }}{{21}}a\).
Chọn C.
Câu hỏi 2 :
Chóp S.ABC, \(SA \bot \left( {ABC} \right),\,\,\Delta ABC\) vuông ở A. \(AB = a,\,\,AC = a\sqrt 2 ;\,\,{S_{\Delta SBC}} = \dfrac{{{a^2}\sqrt {33} }}{6}\). M là trung điểm AB. Tính \(d\left( {M;\left( {SBC} \right)} \right)\).
- A \(\dfrac{{a\sqrt {330} }}{{66}}\)
- B \(\dfrac{{a\sqrt {33} }}{{66}}\)
- C \(\dfrac{{a\sqrt {336} }}{{66}}\)
- D \(\dfrac{{a\sqrt {30} }}{{66}}\)
Đáp án: A
Lời giải chi tiết:
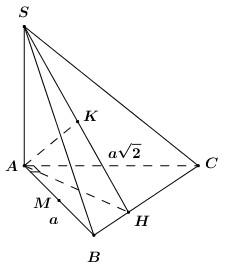
Kẻ \(AH \bot BC\) ta có: \(\left\{ \begin{array}{l}BC \bot AH\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAH} \right)\).
Trong \(\left( {SAH} \right)\) kẻ \(AK \bot SH\) \( \Rightarrow BC \bot AK\).
Do đó \(AK \bot \left( {SBC} \right) \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AK\).
Ta có: \(AM \cap \left( {SBC} \right) = B \Rightarrow \frac{{d\left( {A;\left( {SBC} \right)} \right)}}{{d\left( {M;\left( {SBC} \right)} \right)}} = \frac{{AB}}{{MB}} = 2\).
\( \Rightarrow d\left( {M;\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = \frac{1}{2}AK\).
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{2{a^2}}} = \frac{3}{{2{a^2}}} \Rightarrow AH = \frac{{a\sqrt 6 }}{3}\).
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 \).
\({S_{\Delta SBC}} = \frac{1}{2}SH.BC \Rightarrow SH = \frac{{2{S_{\Delta SBC}}}}{{BC}} = \frac{{2.\frac{{{a^2}\sqrt {33} }}{6}}}{{a\sqrt 3 }} = \frac{{a\sqrt {11} }}{3}\).
Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AH \Rightarrow \Delta SAH\) vuông tại \(A\).
\( \Rightarrow SA = \sqrt {S{H^2} - A{H^2}} = \sqrt {\frac{{11{a^2}}}{9} - \frac{{2{a^2}}}{3}} = \frac{{a\sqrt 5 }}{3}\).
Áp dụng hệ thức lượng trong tam giác vuông \(SAH\) có: \(AK = \frac{{SA.AH}}{{SH}} = \frac{{\frac{{a\sqrt 5 }}{3}.\frac{{a\sqrt 6 }}{3}}}{{\frac{{a\sqrt {11} }}{3}}} = \frac{{a\sqrt {30} }}{{3\sqrt {11} }}\).
Vậy \(d\left( {M;\left( {SBC} \right)} \right) = \frac{{a\sqrt {30} }}{{6\sqrt {11} }} = \frac{{a\sqrt {330} }}{{66}}\).
Chọn A.
Câu hỏi 3 :
Cho hình chóp tứ giác đều \(S.ABCD\), có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là \({60^0}\). Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SCD} \right)\).
- A \(\dfrac{a}{4}\).
- B \(\dfrac{{a\sqrt 3 }}{4}\).
- C \(\dfrac{{a\sqrt 3 }}{2}\).
- D \(\dfrac{a}{2}\).
Đáp án: C
Phương pháp giải:
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\):
- Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\).
- Xác định 1 mặt phẳng \(\left( \gamma \right) \bot \Delta \).
- Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right)\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\): \(\left( {\widehat {\left( \alpha \right);\left( \beta \right)}} \right) = \left( {\widehat {a;b}} \right)\)
Lời giải chi tiết:
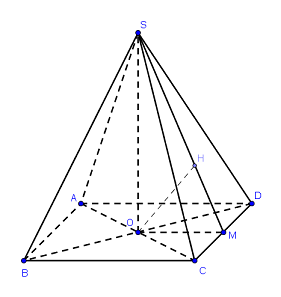
Gọi O là tâm của hình vuông ABCD, M là trung điểm của CD.
\( \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle SMO = {60^0}\)
Dựng \(OH \bot SM \Rightarrow OH \bot \left( {SCD} \right)\).
Do O là trung điểm của BD nên \(d\left( {B;\left( {SCD} \right)} \right) = 2\,d\left( {O;\left( {SCD} \right)} \right) = 2.OH\)
Ta có: \(OM = \dfrac{1}{2}AD = \dfrac{1}{2}a\)
Tam giác OMH vuông tại H, \(\angle SMO = {60^0}\) \( \Rightarrow OH = OM.\sin {60^0} = \dfrac{1}{2}a.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{4}\)\( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = \dfrac{{a\sqrt 3 }}{2}\).
Chọn C.
Câu hỏi 4 :
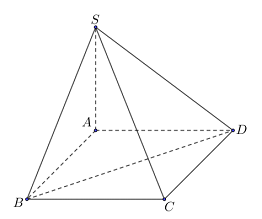
Cho hình chóp tứ giác đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\sqrt 2 ,\) \(SA \bot \left( {ABCD} \right)\) và \(SA = a\). Khoảng cách từ A đến \(\left( {SBD} \right)\) bằng:
- A \(\dfrac{{a\sqrt 2 }}{2}\).
- B \(\dfrac{{a\sqrt 3 }}{2}\).
- C \(\dfrac{a}{2}\).
- D \(\dfrac{{a\sqrt 3 }}{4}\).
Đáp án: A
Phương pháp giải:
- Xác định mặt phẳng \(\left( P \right)\) chứa \(A\) và vuông góc với \(\left( {SBD} \right)\).
- Trong mặt phẳng đó kẻ đoạn thẳng vuông góc với giao tuyến của \(\left( P \right)\) và \(\left( {SBD} \right)\).
- Chứng minh đoạn thẳng vừa kẻ là khoảng cách từ \(A\) đến \(\left( {SBD} \right)\).
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
Gọi \(O = AC \cap BD\). Vì \(ABCD\) là hình vuông nên \(AC \bot BD\) tại \(O\).
Trong \(\left( {SAO} \right)\) kẻ \(AH \bot SO\,\,\left( {H \in SO} \right)\) ta có:
Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot AH\)
Mà \(SO \bot AH \Rightarrow AH \bot \left( {SBD} \right) \Rightarrow d\left( {A;\left( {SBD} \right)} \right) = AH.\)
Tam giác \(SAO\) vuông tại \(A\) (do \(SA \bot \left( {ABCD} \right)\)), đường cao \(AH\), có:
\(\begin{array}{l}SA = a,\,\,AO = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 .\sqrt 2 }}{2} = a\\ \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{O^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{2}{{{a^2}}}\\ \Rightarrow AH = \dfrac{{a\sqrt 2 }}{2}\end{array}\)
Vậy \(d\left( {A;\left( {SBD} \right)} \right) = \dfrac{{a\sqrt 2 }}{2}\).
Chọn A.
Câu hỏi 5 :
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, \(AB = a\), \(AD = 2a\). \(\Delta SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng \(\left( {ABCD} \right)\) bằng \({45^0}\). Gọi \(M\) là trung điểm của \(SD\). Tính theo \(a\) khoảng cách \(d\) từ điểm \(M\) đến mặt phẳng \(\left( {SAC} \right)\).
- A \(d = \dfrac{{a\sqrt {1513} }}{{89}}\)
- B \(d = \dfrac{{2a\sqrt {1513} }}{{89}}\)
- C \(d = \dfrac{{a\sqrt {1315} }}{{89}}\)
- D \(d = \dfrac{{2a\sqrt {1315} }}{{89}}\)
Đáp án: A
Phương pháp giải:
- Chuyển tính khoảng cách từ \(M\) đến mặt phẳng \(\left( {SAC} \right)\) sang tính khoảng cách từ \(H\) đến \(\left( {SAC} \right)\).
- Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
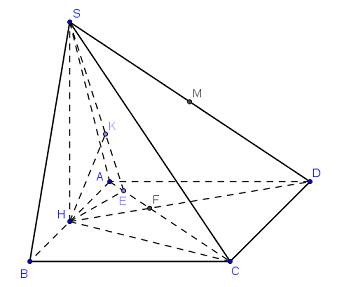
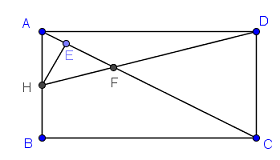
Gọi \(H\) là trung điểm của \(AB\).
Vì \(\Delta SAB\) cân tại \(S\) nên \(SH \bot AB\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SH \bot AB\end{array} \right.\) \( \Rightarrow SH \bot \left( {ABCD} \right)\).
Trong \(\left( {ABCD} \right)\) gọi \(F = AC \cap HD\), dựng \(HE \bot AC\) ta có: \(\left\{ \begin{array}{l}AC \bot HE\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHE} \right)\).
Trong \(\left( {SHE} \right)\) kẻ \(HK \bot SE\) ta có: \(\left\{ \begin{array}{l}HK \bot SE\\HK \bot AC\end{array} \right. \Rightarrow HK \bot \left( {SAC} \right)\)\( \Rightarrow d\left( {H;\left( {SAC} \right)} \right) = HK\).
Ta có: \(M\) là trung điểm của \(SC\) \( \Rightarrow d\left( {M;\left( {SAC} \right)} \right) = \dfrac{1}{2}d\left( {D;\left( {SAC} \right)} \right)\)
Lại có: \(\dfrac{{DF}}{{HF}} = \dfrac{{DC}}{{HA}} = 2\) \( \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right)\)
\( \Rightarrow d\left( {M;\left( {SAC} \right)} \right) = d\left( {H;\left( {SAC} \right)} \right) = HK\)
Ta có: \(\Delta AHE\) đồng dạng \(\Delta ACB\) \(\left( {g.g} \right)\).
\( \Rightarrow \dfrac{{HE}}{{BC}} = \dfrac{{AH}}{{AC}} \Leftrightarrow \dfrac{{HE}}{{2a}} = \dfrac{{\dfrac{a}{2}}}{{\sqrt {{a^2} + 4{a^2}} }} \Leftrightarrow HE = \dfrac{{a\sqrt 5 }}{5}\)
Ta có : \(SH \bot \left( {ABCD} \right)\) nên \(HC\) là hình chiếu của \(SC\) lên \(\left( {ABCD} \right)\).
\( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;HC} \right) = \angle SCH = {45^0}\).
\(\Delta BHC\) vuông tại \(B\) \( \Rightarrow HC = \sqrt {B{C^2} + B{H^2}} = \sqrt {4{{\rm{a}}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt {17} }}{2}\)
\(\Delta SHC\) vuông tại \(H\) \( \Rightarrow SH = HC.\tan {45^0} = \dfrac{{a\sqrt {17} }}{2}\)
Tam giác SHE vuông tại H, HK là đường cao
\( \Rightarrow \dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{E^2}}} = \dfrac{1}{{\dfrac{{17{{\rm{a}}^2}}}{4}}} + \dfrac{1}{{\dfrac{{{a^2}}}{5}}} = \dfrac{{89}}{{17{{\rm{a}}^2}}} \Rightarrow HK = \dfrac{{a\sqrt {1513} }}{{89}}\)
\( \Rightarrow d\left( {M;\left( {SAC} \right)} \right) = d = \dfrac{{a\sqrt {1513} }}{{89}}.\)
Chọn: A.
Câu hỏi 6 :
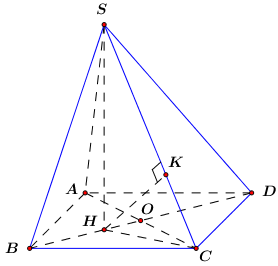
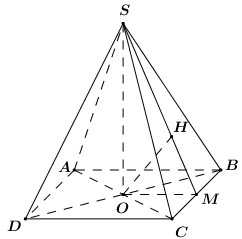
Cho hình chóp \(SABCD\) có đáy là hình thang, \(AB = 2a,\) \(AD = DC = CB = a,\)\(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB.\) Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng:
- A \(\frac{{3a}}{4}\)
- B \(\frac{{3a}}{2}\)
- C \(\frac{{3\sqrt {13} a}}{{13}}\)
- D \(\frac{{6\sqrt {13} a}}{{13}}\)
Đáp án: A
Câu hỏi 7 :
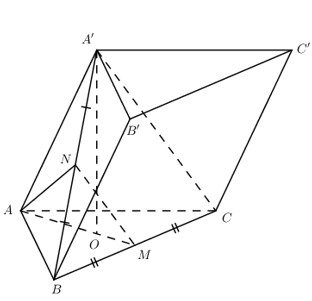
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi E, F lần lượt là trung điểm của AB, CD. Khoảng cách giữa hai đường thẳng EF và AC’ là:
- A \(d = a\)
- B \(d = \dfrac{{\sqrt 2 a}}{4}\)
- C \(d = \dfrac{{\sqrt 2 a}}{2}\)
- D \(d = \dfrac{a}{2}\)
Đáp án: B
Phương pháp giải:
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách giữa đường này và mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
- Sử dụng phương pháp đổi đỉnh, đổi về khoảng cách từ E đến \(\left( {AC'B'} \right)\).
- Xác định khoảng cách và sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
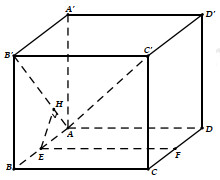
Ta có EF // B’C’ \( \Rightarrow EF\parallel \left( {AC'B'} \right)\) \( \Rightarrow d\left( {EF;AC'} \right) = d\left( {EF;\left( {AC'B'} \right)} \right) = d\left( {E;\left( {AC'B'} \right)} \right)\).
Kẻ \(EH \bot AB'\,\,\left( {H \in AB'} \right)\).
Ta có: \(C'B' \bot \left( {ABB'A'} \right) \Rightarrow B'C' \bot EH\) \( \Rightarrow EH \bot \left( {AC'B'} \right)\).
\( \Rightarrow d\left( {E;\left( {AC'B'} \right)} \right) = EH\).
Xét tam giác AEH vuông cân tại H có: \(EA = \dfrac{a}{2} \Rightarrow EH = \dfrac{{a\sqrt 2 }}{4}\).
Vậy \(d\left( {EF;AC'} \right) = \dfrac{{a\sqrt 2 }}{4}.\)
Chọn B.
Câu hỏi 8 :
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(a\), \(SA\)vuông gócvới mặt phẳng đáy, góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt đáy là \({60^0}\) (minh họa như hình bên). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC\). Khoảng cách giữa hai đường thẳng \(SB\) và \(MN\) bằng:
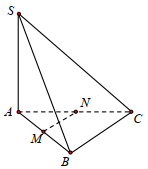
- A \(\dfrac{{3a}}{8}\)
- B \(\dfrac{{3a}}{4}\)
- C \(a\sqrt 6 \)
- D \(\dfrac{{a\sqrt 6 }}{2}\)
Đáp án: A
Phương pháp giải:
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách giữa đường này và mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
- Sử dụng phương pháp đổi đỉnh, đổi về khoảng cách từ \(A\) đến \(\left( {SBC} \right)\).
- Xác định khoảng cách và sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên \(MN\parallel BC \Rightarrow MN\parallel \left( {SBC} \right)\).
\( \Rightarrow d\left( {MN;SB} \right) = d\left( {MN;\left( {SBC} \right)} \right) = d\left( {M;\left( {SBC} \right)} \right)\).
Ta có:
\(\begin{array}{l}AM \cap \left( {SBC} \right) = B \Rightarrow \dfrac{{d\left( {M;\left( {SBC} \right)} \right)}}{{d\left( {A;\left( {SBC} \right)} \right)}} = \dfrac{{MB}}{{AB}} = \dfrac{1}{2}\\ \Rightarrow d\left( {M;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right)\end{array}\)
Gọi \(K\) là trung điểm của \(BC\). Vì \(\Delta ABC\) đều nên \(BC \bot AK\).
Ta có: \(\left\{ \begin{array}{l}BC \bot AK\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right.\)\( \Rightarrow BC \bot \left( {SAK} \right)\).
Trong \(\left( {SAK} \right)\) kẻ \(AH \bot SK\,\,\left( {H \in SK} \right)\), ta có: \(\left\{ \begin{array}{l}AH \bot SK\\AH \bot BC\end{array} \right.\)\( \Rightarrow AH \bot \left( {SBC} \right)\).
\( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH\).
Tam giác \(ABC\) đều cạnh \(a\) nên \(AK = \dfrac{{a\sqrt 3 }}{2}\).
Ta có: \(BC \bot \left( {SAK} \right) \Rightarrow BC \bot SK\).
Khi đó ta có \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SK \bot BC\\\left( {ABC} \right) \supset AK \bot BC\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SK;AK} \right) = \angle SKA = {60^0}\).
Xét tam giác vuông \(SAK\) có: \(SA = AK.tan{60^0} = \dfrac{{a\sqrt 3 }}{2}.\sqrt 3 = \dfrac{{3a}}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông \(SAK\) ta có:
\(AH = \dfrac{{SA.AK}}{{\sqrt {S{A^2} + A{K^2}} }} = \dfrac{{\dfrac{{3a}}{2}.\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {\dfrac{{9{a^2}}}{4} + \dfrac{{3{a^2}}}{4}} }} = \dfrac{{3a}}{4}\).
Vậy \(d\left( {MN;SB} \right) = \dfrac{1}{2}AH = \dfrac{{3a}}{8}\).
Chọn A.
Câu hỏi 9 :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy (ABCD), biết SD = \(2a\sqrt 5 \), SC tạo với mặt đáy (ABCD) một góc bằng 600. Khoảng cách từ A đến mp(SCD) bằng ?
- A \(\dfrac{{2a\sqrt {15} }}{{\sqrt {79} }}\).
- B \(\dfrac{{a\sqrt {15} }}{{\sqrt {19} }}\).
- C \(\dfrac{{2a\sqrt {15} }}{{\sqrt {19} }}\).
- D \(\dfrac{{a\sqrt {15} }}{{\sqrt {79} }}\).
Đáp án: C
Phương pháp giải:
- Chứng minh \(SM \bot \left( {ABCD} \right)\).
- Sử dụng định lí: \(AB\parallel \left( P \right) \Rightarrow d\left( {A;\left( P \right)} \right) = d\left( {B;\left( P \right)} \right)\), đổi đỉnh tính khoảng cách từ M đến (SCD).
- Gọi N là trung điểm của CD, trong (SMN) dựng \(MH \bot SN\), chứng minh \(MH \bot \left( {SCD} \right)\).
- Đặt \(AB = x\), tính MC, MD theo x.
- Xác định góc giữa SC và (ABCD) là góc giữa SC và hình chiếu của SC lên (ABCD), từ đó tính SM theo x.
- Áp dụng định lí Pytago trong tam giác vuông SMD tìm x, từ đó tính được SM và MN theo a.
- Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
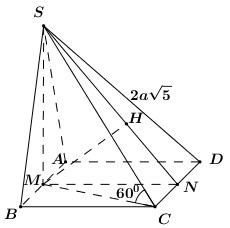
Vì tam giác SAB cân tại S nên \(SM \bot AB\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SM \subset \left( {SAB} \right),\,\,SM \bot AB\end{array} \right.\) \( \Rightarrow SM \bot \left( {ABCD} \right)\).
\( \Rightarrow MC\) là hình chiếu của SC lên (ABCD) \( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;MC} \right) = \angle SCM = {60^0}\).
Gọi N là trung điểm của CD \( \Rightarrow MN \bot CD\).
Trong (SMN) kẻ \(MH \bot SN\,\,\left( {H \in SN} \right)\).
Ta có: \(\left\{ \begin{array}{l}CD \bot MN\\CD \bot SM\,\,\left( {SM \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow CD \bot \left( {SMN} \right) \Rightarrow CD \bot MH\).
\(\left\{ \begin{array}{l}MH \bot CD\\MH \bot SN\end{array} \right. \Rightarrow MH \bot \left( {SCD} \right)\) \( \Rightarrow d\left( {M;\left( {SCD} \right)} \right) = MH\).
Ta có: \(AM\parallel CD \Rightarrow AM\parallel \left( {SCD} \right)\), do đó \(d\left( {A;\left( {SCD} \right)} \right) = d\left( {M;\left( {SCD} \right)} \right) = MH\).
Gọi cạnh của hình vuông ABCD bằng x.
Áp dụng định lí Pytago ta có: \(MC = MD = \sqrt {{x^2} + \dfrac{{{x^2}}}{4}} = \dfrac{{x\sqrt 5 }}{2}\).
Xét tam giác vuông SMC có: \(SM = MC.\tan {60^0} = \dfrac{{x\sqrt {15} }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông SMD có:
\(\begin{array}{l}S{M^2} + M{D^2} = S{D^2}\\ \Leftrightarrow \dfrac{{15{x^2}}}{4} + \dfrac{{5{x^2}}}{4} = 20{a^2}\\ \Leftrightarrow 5{x^2} = 20{a^2}\\ \Leftrightarrow {x^2} = 4{a^2} \Leftrightarrow x = 2a\end{array}\)
\( \Rightarrow MN = x = 2a\) và \(SM = \dfrac{{2a.\sqrt {15} }}{2} = a\sqrt {15} \).
Áp dụng hệ thức lượng trong tam giác vuông SMN có:
\(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{S{M^2}}} + \dfrac{1}{{M{N^2}}} = \dfrac{1}{{15{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{{19}}{{60{a^2}}}\) \( \Rightarrow MH = \dfrac{{2a\sqrt {285} }}{{19}}\).
Vậy \(d\left( {A;\left( {SCD} \right)} \right) = \dfrac{{2a\sqrt {285} }}{{19}} = \dfrac{{2a\sqrt {15} }}{{\sqrt {19} }}\).
Chọn C.
Câu hỏi 10 :
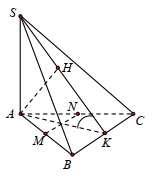
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên bằng a, gọi O là tâm của đáy ABCD. Khoảng cách từ O đến mặt phẳng (SBC) bằng ?
- A \(\dfrac{{3a}}{2}\).
- B \(\dfrac{{a\sqrt 6 }}{3}\).
- C \(\dfrac{{a\sqrt 6 }}{6}\).
- D \(\dfrac{{a\sqrt 3 }}{6}\).
Đáp án: C
Phương pháp giải:
- Gọi M là trung điểm của BC, trong (SOM) kẻ \(OH \bot SM\,\,\left( {H \in SM} \right)\), chứng minh \(OH \bot \left( {SBC} \right)\).
- Áp dụng định lí Pytago và hệ thức lượng trong tam giác vuông tính khoảng cách.
Lời giải chi tiết:
Gọi M là trung điểm của BC, suy ra OM là đường trung bình của tam giác ABC.
\( \Rightarrow OM\parallel AB\), mà \(AB \bot BC\) \( \Rightarrow OM \bot BC\) và \(OM = \dfrac{1}{2}AB = \dfrac{a}{2}\).
Ta có: \(\left\{ \begin{array}{l}BC \bot OM\\BC \bot SO\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SOM} \right)\).
Trong (SOM) kẻ \(OH \bot SM\,\,\left( {O \in SM} \right)\), ta có:
\(\left\{ \begin{array}{l}BC \bot \left( {SOM} \right) \Rightarrow BC \bot OH\\OH \bot SM\end{array} \right.\) \( \Rightarrow OH \bot \left( {SBC} \right)\) \( \Rightarrow d\left( {O;\left( {SBC} \right)} \right) = OH\).
Tam giác SBC đều cạnh a nên \(SM = \dfrac{{a\sqrt 3 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông SOM có: \(SO = \sqrt {S{M^2} - O{M^2}} = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{4}} = \dfrac{a}{{\sqrt 2 }}\).
Áp dụng hệ thức lượng trong tam giác vuông SOM có: \(OH = \dfrac{{SO.OM}}{{SM}} = \dfrac{{\dfrac{a}{{\sqrt 2 }}.\dfrac{a}{2}}}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{a\sqrt 6 }}{6}\).
Vậy \(d\left( {O;\left( {SBC} \right)} \right) = \dfrac{{a\sqrt 6 }}{6}\).
Chọn C.
Câu hỏi 11 :
Cho chóp tứ giác đều S.ABCD có AB = a và \(SB = \dfrac{{a\sqrt 3 }}{2}\). Tính khoảng cách từ A đến mặt phẳng (SBC).
- A \(d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{a\sqrt 2 }}{4}\)
- B \(d\left( {A;\left( {SBC} \right)} \right) = \dfrac{a}{2}\)
- C \(d\left( {A;\left( {SBC} \right)} \right) = a\)
- D \(d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{a\sqrt 2 }}{2}\)
Đáp án: D
Phương pháp giải:
- Đổi điểm về tính khoảng cách từ O đến (SBC).
- Xác định mặt phẳng chứa O và vuông góc với (SBC).
- Trong mặt phẳng đó kẻ đường thẳng vuông góc với giao tuyến của mặt phẳng đó và (SBC).
- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông.
Lời giải chi tiết:
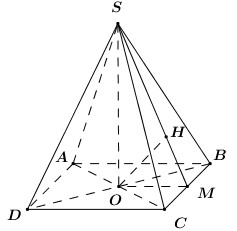
Gọi \(O = AC \cap BD\). Vì chóp S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\).
Ta có: \(AO \cap \left( {SBC} \right) = C \Rightarrow \dfrac{{d\left( {A;\left( {SBC} \right)} \right)}}{{d\left( {O;\left( {SBC} \right)} \right)}} = \dfrac{{AC}}{{OC}} = 2\).
\( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 2d\left( {O;\left( {SBC} \right)} \right)\).
Gọi M là trung điểm của BC, suy ra OM là đường trung bình của tam giác ABC.
\( \Rightarrow OM\parallel AB\) và \(OM = \dfrac{1}{2}BC = \dfrac{1}{2}AB = \dfrac{a}{2}\). Mà \(AB \bot BC\) nên \(OM \bot BC\).
Ta có: \(\left\{ \begin{array}{l}BC \bot OM\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOM} \right)\).
\(\left\{ \begin{array}{l}BC \bot \left( {SOM} \right)\\BC \subset \left( {SBC} \right)\end{array} \right. \Rightarrow \left( {SOM} \right) \bot \left( {SBC} \right)\) và \(\left( {SOM} \right) \cap \left( {SBC} \right) = SM\).
Trong (SOM) kẻ \(OH \bot SM\) ta có:
\(\left\{ \begin{array}{l}\left( {SBC} \right) \bot \left( {SOM} \right)\\\left( {SBC} \right) \cap \left( {SOM} \right) = SM\\OH \subset \left( {SOM} \right),\,\,OH \bot SM\end{array} \right. \Rightarrow OH \bot \left( {SBC} \right)\).
Do đó \(d\left( {O;\left( {SBC} \right)} \right) = OH\) và \(d\left( {A;\left( {SBC} \right)} \right) = 2OH\).
Vì ABCD là hình vuông cạnh a nên \(AC = BD = a\sqrt 2 \) \( \Rightarrow OB = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông SOB có: \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{2{a^2}}}{4}} = \dfrac{a}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông SOM có: \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{M^2}}} = \dfrac{4}{{{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{8}{{{a^2}}}\) \( \Rightarrow OH = \dfrac{{a\sqrt 2 }}{4}\).
Vậy \(d\left( {A;\left( {SBC} \right)} \right) = 2OH = \dfrac{{a\sqrt 2 }}{2}\).
Chọn D.
Câu hỏi 12 :
Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc, \(OA = OB = a\), \(OC = 2a\). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(OM\) và \(AC\) bằng:
- A \(\dfrac{{2\sqrt 5 a}}{5}\)
- B \(\dfrac{{a\sqrt 2 }}{2}\)
- C \(\dfrac{{a\sqrt 2 }}{3}\)
- D \(\dfrac{{2a}}{3}\)
Đáp án: D
Phương pháp giải:
- Gọi \(D\) là điểm đối xứng với \(B\) qua \(O\). Chứng minh \(d\left( {OM;AC} \right) = d\left( {O;\left( {ACD} \right)} \right)\).
- Sử dụng công thức giải nhanh: Tứ giác \(OACD\) có \(OA,\,\,OC,\,\,OD\) đôi một vuông góc nên \(\dfrac{1}{{{d^2}\left( {O;\left( {ACD} \right)} \right)}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{D^2}}}\).
Lời giải chi tiết:
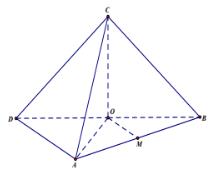
Gọi \(D\) là điểm đối xứng với \(B\) qua \(O\).
Ta có: \(OM\) là đường trung bình của tam giác \(ABD\) nên \(OM\parallel AD \Rightarrow OM\parallel \left( {ACD} \right)\).
\( \Rightarrow d\left( {OM;AC} \right) = d\left( {OM;\left( {ACD} \right)} \right) = d\left( {O;\left( {ACD} \right)} \right)\).
Vì tứ giác \(OACD\) có \(OA,\,\,OC,\,\,OD\) đôi một vuông góc nên \(\dfrac{1}{{{d^2}\left( {O;\left( {ACD} \right)} \right)}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{D^2}}} = \dfrac{9}{{4{a^2}}}\).
\( \Rightarrow d\left( {O;\left( {ACD} \right)} \right) = \dfrac{{2a}}{3}\).
Vậy \(d\left( {OM;AC} \right) = \dfrac{{2a}}{3}\).
Chọn D.
Câu hỏi 13 :
Cho hình chóp S.ABC có SA = a, tam giác ABC đều, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ B đế mặt phẳng (SAC) bằng:
- A \(\dfrac{{a\sqrt {42} }}{7}\)
- B \(\dfrac{{a\sqrt {42} }}{{14}}\)
- C \(\dfrac{{a\sqrt {42} }}{{12}}\)
- D \(\dfrac{{a\sqrt {42} }}{6}\)
Đáp án: A
Phương pháp giải:
- Gọi H là trung điểm của AB, chứng minh \(SH \bot \left( {ABC} \right)\).
- Sử dụng phương pháp đổi đỉnh, đổi sang tính khoảng cách từ H đến (SAC).
- Sử dụng phương pháp 3 nét để dựng khoảng cách từ chân đường cao đến mặt bên.
- Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
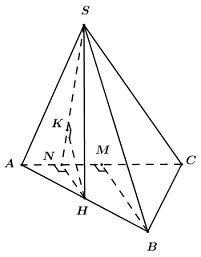
Gọi H là trung điểm của AB, do tam giác SAB vuông cân tại S nên \(SH \bot AB\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right) = AB\\SH \subset \left( {SAB} \right);\,\,SH \bot AB\end{array} \right.\) \( \Rightarrow SH \bot \left( {ABC} \right)\).
Gọi M, N lần lượt là trung điểm của AC, AM. Do tam giác ABC đều nên \(BM \bot AC\), mà \(HN\parallel BM\) (do HN là đường trung bình của tam giác ABM) \( \Rightarrow HN \bot AC\).
Trong (SHN) kẻ \(HK \bot SN\,\,\left( {K \in SN} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}AC \bot HN\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHN} \right) \Rightarrow AC \bot HK\\\left\{ \begin{array}{l}HK \bot SN\\HK \bot AC\end{array} \right. \Rightarrow HK \bot \left( {SAC} \right)\\ \Rightarrow d\left( {H;\left( {SAC} \right)} \right) = HK\end{array}\)
Lại có: \(BH \cap \left( {SAC} \right) = A \Rightarrow \dfrac{{d\left( {B;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \dfrac{{BA}}{{HA}} = 2\).
\( \Rightarrow d\left( {B;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right) = 2HK\).
Tam giác SAB vuông cân tại S, có SA = a \( \Rightarrow AB = SA\sqrt 2 = a\sqrt 2 \) và \(SH = \dfrac{1}{2}AB = \dfrac{{a\sqrt 2 }}{2}\).
\( \Rightarrow \) Tam giác ABC đều cạnh \(a\sqrt 2 \) \( \Rightarrow BM = a\sqrt 2 .\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{2}\) \( \Rightarrow HN = \dfrac{1}{2}BM = \dfrac{{a\sqrt 6 }}{4}\).
Áp dụng hệ thức lượng trong tam giác vuông SHN có:
\(HK = \dfrac{{SH.HN}}{{\sqrt {S{H^2} + H{N^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.\dfrac{{a\sqrt 6 }}{4}}}{{\sqrt {\dfrac{{{a^2}}}{2} + \dfrac{{3{a^2}}}{8}} }} = \dfrac{{a\sqrt {42} }}{{14}}\).
Vậy \(d\left( {B;\left( {SAC} \right)} \right) = 2HK = \dfrac{{a\sqrt {42} }}{7}\).
Chọn A.
Câu hỏi 14 :
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD = 2a. Cạnh bên SA vuông góc với đáy, SA = 2a. Khoảng cách giữa hai đường thẳng AB và SD bằng:
- A \(a\sqrt 2 \)
- B \(\dfrac{{2a}}{{\sqrt 5 }}\)
- C \(2a\)
- D \(a\)
Đáp án: A
Phương pháp giải:
- Sử dụng định lí: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường thứ nhất đến mặt phẳng song song với nó và chứa đường thứ hai.
- Quy về bài toán tính khoảng cách từ chân đường vuông góc đến mặt phẳng.
- Dựng khoảng cách, sử dụng tính chất tam giác vuông cân hoặc hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
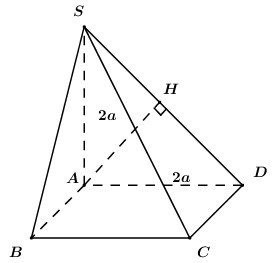
Ta có: \(AB\parallel CD\,\,\left( {gt} \right) \Rightarrow AB\parallel \left( {SCD} \right) \supset SD\).
\( \Rightarrow d\left( {AB;SD} \right) = d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\).
Trong (SAD) kẻ \(AH \bot SD\,\,\left( {H \in SD} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AH\\\left\{ \begin{array}{l}AH \bot SD\\AH \bot CD\end{array} \right. \Rightarrow AH \bot \left( {SCD} \right)\\ \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AH\\ \Rightarrow d\left( {AB;SD} \right) = AH\end{array}\)
Vì tam giác SAD vuông cân tại A có \(SA = AD = 2a \Rightarrow AH = \dfrac{{SA}}{{\sqrt 2 }} = a\sqrt 2 \).
Vậy \(d\left( {AB;SD} \right) = a\sqrt 2 \).
Chọn A.
Câu hỏi 15 :
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 2a, BC = a, tam giác đều SAB nằm trên mặt phẳng vuông góc với đáy. Khoảng cách giữa BC và SD là:
- A \(\sqrt 3 a\)
- B \(\dfrac{{\sqrt 3 }}{2}a\)
- C \(\dfrac{{2\sqrt 5 }}{5}a\)
- D \(\dfrac{{\sqrt 5 }}{5}a\)
Đáp án: A
Phương pháp giải:
- Gọi H là trung điểm của AB, chứng minh \(SH \bot \left( {ABCD} \right)\).
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng chứa đường thẳng kia và song song với đường thẳng này. Từ đó chứng minh \(d\left( {BC;SD} \right) = d\left( {BC;\left( {SAD} \right)} \right) = d\left( {B;\left( {SAD} \right)} \right)\).
- Sử dụng phương pháp đổi điểm: \(AB \cap \left( P \right) = M \Rightarrow \dfrac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}} = \dfrac{{AM}}{{BM}}\), đổi về tính khoảng cách từ chân đường vuông góc.
- Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
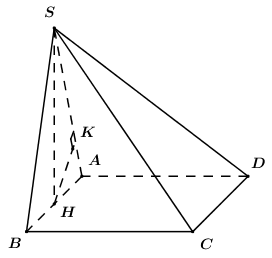
Gọi H là trung điểm của AB, do tam giác SAB đều nên \(SH \bot AB\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SH \subset \left( {SAB} \right),\,\,SH \bot AB\end{array} \right.\) \( \Rightarrow SH \bot \left( {ABCD} \right)\).
Vì ABCD là hình chữ nhật nên \(BC\parallel AD \Rightarrow BC\parallel \left( {SAD} \right) \supset SD\).
\( \Rightarrow d\left( {BC;SD} \right) = d\left( {BC;\left( {SAD} \right)} \right) = d\left( {B;\left( {SAD} \right)} \right)\).
Ta có: \(BH \cap \left( {SAD} \right) = A \Rightarrow \dfrac{{d\left( {B;\left( {SAD} \right)} \right)}}{{d\left( {H;\left( {SAD} \right)} \right)}} = \dfrac{{BA}}{{HA}} = 2\).
\( \Rightarrow d\left( {B;\left( {SAD} \right)} \right) = 2d\left( {H;\left( {SAD} \right)} \right)\).
Trong (SAB) kẻ \(HK \bot SA\,\,\left( {K \in SA} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}AD \bot SH\\AD \bot AB\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right) \Rightarrow AD \bot HK\\\left\{ \begin{array}{l}HK \bot SA\\HK \bot AD\end{array} \right. \Rightarrow HK \bot \left( {SAD} \right)\\ \Rightarrow d\left( {H;\left( {SAD} \right)} \right) = HK\end{array}\)
Tam giác SAB đều cạnh 2a nên \(SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).
Áp dụng hệ thức lượng trong tam giác vuông SAH có: \(HK = \dfrac{{SH.AH}}{{\sqrt {S{H^2} + A{H^2}} }} = \dfrac{{a\sqrt 3 .a}}{{\sqrt {3{a^2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{2}\).
Vậy \(d\left( {BC;SD} \right) = 2HK = a\sqrt 3 \).
Chọn A.
Câu hỏi 16 :
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Biết \(\Delta SAC\) cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc \(\angle SBC = {60^0}\). Gọi H là trung điểm AC. Tính khoảng cách từ H đến (SBC).
- A \({d_{\left[ {H;\left( {SBC} \right)} \right]}} = \dfrac{{a\sqrt 6 }}{6}\).
- B \({d_{\left[ {H;\left( {SBC} \right)} \right]}} = \dfrac{{a\sqrt 6 }}{3}\).
- C \({d_{\left[ {H;\left( {SBC} \right)} \right]}} = \dfrac{{a\sqrt 6 }}{2}\).
- D \({d_{\left[ {H;\left( {SBC} \right)} \right]}} = \dfrac{{a\sqrt 3 }}{6}\).
Đáp án: A
Phương pháp giải:
- Chứng minh \(SH \bot \left( {ABC} \right)\).
- Gọi M, N lần lượt là trung điểm của BC, MC. Chứng minh \(BC \bot \left( {SHN} \right)\).
- Trong (SHN) kẻ , chứng minh \(HK = {d_{\left[ {H;\left( {SBC} \right)} \right]}}\).
- Sử dụng tỉ số lượng giác của góc nhọn, định lí Pytago, hệ thức lượng trong tam giác vuông để tính HK.
Lời giải chi tiết:
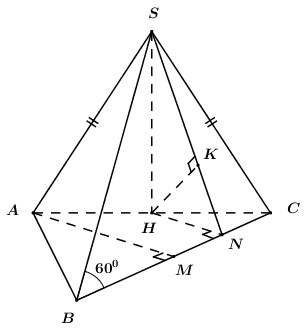
+ \(\Delta SAC\) cân tại S \( \Rightarrow SH \bot AC\).
+ \(\left\{ \begin{array}{l}\left( {SAC} \right) \bot \left( {ABC} \right) = AC\\SH \subset \left( {SAC} \right);\,\,SH \bot AC\end{array} \right.\) \( \Rightarrow SH \bot \left( {ABC} \right)\).
Gọi M, N lần lượt là trung điểm của BC, MC.
+ đều \( \Rightarrow AM \bot BC\) , HN là đường trung bình của tam giác ACM \( \Rightarrow HN\parallel AM\).
\( \Rightarrow HN \bot BC\).
+ \(\left\{ \begin{array}{l}BC \bot HN\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SHN} \right)\).
Trong (SHN) kẻ \(HK \bot SN\) \(\left( {K \in SN} \right)\).
+ \(\left\{ \begin{array}{l}HK \bot SN\\HK \bot BC\,\,\left( {BC \bot \left( {SHN} \right)} \right)\end{array} \right. \Rightarrow HK \bot \left( {SBC} \right)\).
\( \Rightarrow {d_{\left[ {H;\left( {SBC} \right)} \right]}} = HK\).
+ \(\Delta ABC\) đều cạnh a \( \Rightarrow AM = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow HN = \dfrac{{a\sqrt 3 }}{4}\).
+ : \(BN = \dfrac{3}{4}BC = \dfrac{{3a}}{4}\) \( \Rightarrow SN = BN.\tan {60^0} = \dfrac{{3a\sqrt 3 }}{4}\).
+ \(\Delta SHN\): \(SH = \sqrt {S{N^2} - H{N^2}} = \sqrt {\dfrac{{27{a^2}}}{{16}} - \dfrac{{3{a^2}}}{{16}}} = \dfrac{{a\sqrt 6 }}{2}\).
\(HK = \dfrac{{SH.HN}}{{\sqrt {S{H^2} + H{N^2}} }} = \dfrac{{\dfrac{{a\sqrt 6 }}{2}.\dfrac{{a\sqrt 3 }}{4}}}{{\sqrt {\dfrac{{3{a^2}}}{2} + \dfrac{{3{a^2}}}{{16}}} }} = \dfrac{{a\sqrt 6 }}{6}\).
Vậy \({d_{\left[ {H;\left( {SBC} \right)} \right]}} = \dfrac{{a\sqrt 6 }}{6}\).
Câu hỏi 17 :
Cho hình chóp \(SABCD\) có đáy là hình thang, \(AB = 2a,\) \(AD = DC = CB = a,\)\(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB.\) Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng:
- A \(\dfrac{{3a}}{4}\)
- B \(\dfrac{{3a}}{2}\)
- C \(\dfrac{{3\sqrt {13} a}}{{13}}\)
- D \(\dfrac{{6\sqrt {13} a}}{{13}}\)
Đáp án: A
Phương pháp giải:
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng song song với đường thẳng này và chứa đường thẳng kia.
- Đổi về khoảng cách từ đỉnh A.
- Chứng minh \(BC \bot \left( {SAC} \right)\), từ đó dựng khoảng cách từ \(A\) đến \(\left( {SBC} \right).\)
- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
Vì \(\left\{ \begin{array}{l}CD = BM = a\\CD\parallel BM\end{array} \right.\,\,\left( {gt} \right)\) nên \(BCDM\) là hình bình hành (dhnb).
\( \Rightarrow DM\parallel BC\) (2 cạnh đối của hình bình hành).
Mà \(BC \subset \left( {SCD} \right)\) \( \Rightarrow DM\parallel \left( {SBC} \right) \supset SB\).
\( \Rightarrow d\left( {SB;DM} \right) = d\left( {DM;\left( {SBC} \right)} \right) = d\left( {M;\left( {SBC} \right)} \right)\).
Ta có: \(AM \cap \left( {SBC} \right) = B \Rightarrow \dfrac{{d\left( {M;\left( {SBC} \right)} \right)}}{{d\left( {A;\left( {SBC} \right)} \right)}} = \dfrac{{MB}}{{AB}} = \dfrac{1}{2}\).
\( \Rightarrow d\left( {M;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right)\).
Chứng minh tương tự ta có: \(ADCM\) là hình bình hành .
Khi đó ta có \(CM = \dfrac{1}{2}AB\,\,\left( { = a} \right)\), do đó \(\Delta ACB\) vuông tại \(C\) (định lí đường trung tuyến trong tam giác).
\( \Rightarrow AC \bot BC\).
Ta có: \(\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAC} \right)\).
Trong \(SAC\) kẻ \(AH \bot SC\,\,\left( {H \in SC} \right)\) ta có:
\(\left\{ \begin{array}{l}AH \bot BC\,\,\,\left( {BC \bot \left( {SAC} \right)} \right)\\AH \bot SC\end{array} \right.\) \( \Rightarrow AH \bot \left( {SBC} \right)\) \( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH\) \( \Rightarrow d\left( {DM;SB} \right) = \dfrac{1}{2}AH\).
Áp dụng định lí Pytago trong tam giác vuông \(ACD\) ta có:
\(AC = \sqrt {A{B^2} - B{C^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \).
Áp dụng hệ thức lượng trong tam giác vuông \(SAC\,\,\left( {SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC} \right)\) ta có:
\(\begin{array}{l}\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{9{a^2}}} + \dfrac{1}{{3{a^2}}} = \dfrac{4}{{9{a^2}}}\\ \Rightarrow AH = \dfrac{{3a}}{2}\end{array}\)
Vậy \(d\left( {DM;SB} \right) = \dfrac{1}{2}AH = \dfrac{{3a}}{4}\).
Chọn A.
Câu hỏi 18 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\). \(AB = AD = 2a;DC = a\) . Điểm \(I\) là trung điểm đoạn\(AD\), mặt phẳng \(\left( {SIB} \right)\) và \(\left( {SIC} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Mặt phẳng \(\left( {SBC} \right)\) tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc \(60^\circ \). Tính khoảng cách từ \(D\) đến\(\left( {SBC} \right)\) theo \(a\).
- A \(\dfrac{{a\sqrt {15} }}{5}\).
- B \(\dfrac{{9a\sqrt {15} }}{{10}}\).
- C \(\dfrac{{2a\sqrt {15} }}{5}\).
- D \(\dfrac{{9a\sqrt {15} }}{{20}}\).
Đáp án: A
Phương pháp giải:
- Sử dụng định lí: Hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng sẽ vuông góc với mặt phẳng thứ ba đó để chứng minh \(SI \bot \left( {ABCD} \right)\).
- Đổi về bài toán tính khoảng cách từ chân đường cao đến mặt phẳng (SBC).
- Tìm góc giữa mặt phẳng \(\left( {SBC} \right);\left( {ABCD} \right)\): Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
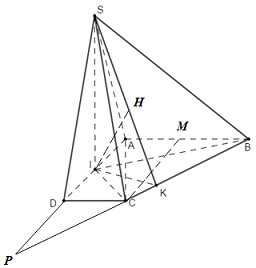
Ta có \(\left\{ \begin{array}{l}\left( {SBI} \right) \bot \left( {ABC{\rm{D}}} \right)\\\left( {SIC} \right) \bot \left( {ABC{\rm{D}}} \right)\\\left( {SIB} \right) \cap \left( {SIC} \right) = SI\end{array} \right. \Rightarrow SI \bot \left( {ABC{\rm{D}}} \right)\)
Trong (ABCD) kéo dài DI cắt BC tại P, khi đó ta có \(DI \cap \left( {SBC} \right) = P\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{PD}}{{PA}} = \dfrac{{CD}}{{AB}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\) \( \Rightarrow D\) là trung điểm của AP.
\( \Rightarrow DP = AD = 2a,\,\,IP = ID + DP = a + 2a = 3a\).
\(\begin{array}{l} \Rightarrow \dfrac{{DP}}{{IP}} = \dfrac{{2a}}{{3a}} = \dfrac{2}{3}\\ \Rightarrow \dfrac{{d\left( {D;\left( {SBC} \right)} \right)}}{{d\left( {I;\left( {SBC} \right)} \right)}} = \dfrac{{DP}}{{IP}} = \dfrac{2}{3}\\ \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = \dfrac{2}{3}d\left( {I;\left( {SBC} \right)} \right).\end{array}\)
Trong (ABCD) kẻ \(IK \bot BC\,\,\left( {K \in BC} \right)\), trong (SIK) kẻ \(IH \bot SK\,\,\left( {H \in SK} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot SI\\BC \bot IK\end{array} \right. \Rightarrow BC \bot \left( {SIK} \right) \Rightarrow BC \bot IH\\\left\{ \begin{array}{l}IH \bot BC\\IH \bot SK\end{array} \right. \Rightarrow IH \bot \left( {SBC} \right) \Rightarrow d\left( {I;\left( {SBC} \right)} \right) = IH\end{array}\)
Ta có hình thang ABCD vuông tại A và D có \(ID = IA = \dfrac{{AD}}{2} = a;\) \(DC = a;\) \(AB = 2a\).
Áp dụng định lí Pytago ta có:
\(\begin{array}{l}IC = \sqrt {I{D^2} + C{D^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \\IB = \sqrt {I{A^2} + A{B^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \end{array}\)
Kẻ \(CM \bot AB\) ta có: AMCD là hình chữ nhật nên \(CM = AD = 2a\), \(MB = AB - AM = 2a - a = a\).
Áp dụng định lí Pytago trong tam giác vuông BCM có: \(BC = \sqrt {B{M^2} + C{M^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \).
Trong (ABCD) kẻ \(IK \bot BC\,\,\left( {K \in BC} \right)\) ta có:
\(\begin{array}{l}{S_{BIC}} = \dfrac{1}{2}IK.BC = {S_{ABCD}} - {S_{DIC}} - {S_{ABI}}\\\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}.AD.\left( {AB + CD} \right) - \dfrac{1}{2}ID.CD - \dfrac{1}{2}IA.AB\\\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}.2a.\left( {2a + a} \right) - \dfrac{1}{2}.a.a - \dfrac{1}{2}.a.2a\\\,\,\,\,\,\,\,\,\,\, = 3{a^2} - \dfrac{1}{2}{a^2} - {a^2} = \dfrac{{3{a^2}}}{2}\end{array}\)
Lại có
\(\begin{array}{l}{S_{BIC}} = \dfrac{1}{2}IK.BC\\ \Rightarrow \dfrac{{3{a^2}}}{2} = \dfrac{1}{2}.IK.a\sqrt 5 \\ \Rightarrow IK = \dfrac{{3a\sqrt 5 }}{5}.\end{array}\)
Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\SK \subset \left( {SBC} \right),\,\,SK \bot BC\\IK \subset \left( {ABCD} \right),\,\,IK \bot BC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {SK;IK} \right) = \angle SKI = {60^0}\).
Xét tam giác vuông IHK có: \(IH = IK.\sin \angle SKI = \dfrac{{3a\sqrt 5 }}{5}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a\sqrt {15} }}{{10}}\).
Vậy \(d\left( {D;\left( {SBC} \right)} \right) = \dfrac{2}{3}d\left( {I;\left( {SBC} \right)} \right) = \dfrac{2}{3}IH = \dfrac{{a\sqrt {15} }}{5}.\)
Chọn A.
Câu hỏi 19 :
Cho tứ diện \(OABC\)có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc, gọi \(M\) là trung điểm của \(BC\) (tham khảo hình vẽ bên). Biết \(OA = a,\)\(OB = OC = a\sqrt 2 \), khoảng cách giữa hai đường thẳng \(AB\) và \(OM\) bằng:
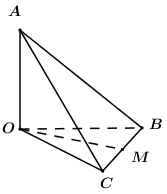
- A \(\dfrac{a}{2}\)
- B \(a\)
- C \(\dfrac{{a\sqrt 2 }}{2}\)
- D \(a\sqrt 2 \)
Đáp án: C
Phương pháp giải:
- Xác định \(\left( P \right)\) chứa \(AB\) và song song với \(OM\), khi đó \(d\left( {OM;AB} \right) = d\left( {OM;\left( P \right)} \right) = d\left( {O;\left( P \right)} \right)\).
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
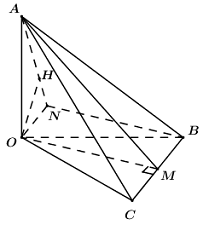
Trong \(\left( {OBC} \right)\) dựng hình bình hành \(OMBN\) như hình vẽ, ta có \(BN\parallel OM \Rightarrow OM\parallel \left( {ABN} \right) \supset AB\).
\( \Rightarrow d\left( {OM;AB} \right) = d\left( {OM;\left( {ABN} \right)} \right) = d\left( {O;\left( {ABN} \right)} \right)\).
Vì \(OB = OC = a\sqrt 2 \Rightarrow \Delta OBC\) cân tại \(O\) \( \Rightarrow OM \bot BC\) \( \Rightarrow OMBN\) là hình chữ nhật \( \Rightarrow ON \bot BN\).
Ta có: \(\left\{ \begin{array}{l}BN \bot ON\\BN \bot OA\,\,\left( {OA \bot \left( {OBC} \right)} \right)\end{array} \right. \Rightarrow BN \bot \left( {OAN} \right)\).
Trong \(\left( {OAN} \right)\) kẻ \(OH \bot AN\,\,\left( {H \in AN} \right)\) ta có: \(\left\{ \begin{array}{l}OH \bot AN\\OH \bot BN\end{array} \right. \Rightarrow OH \bot \left( {ABN} \right) \Rightarrow d\left( {O;\left( {ABN} \right)} \right) = OH\).
\( \Rightarrow d\left( {OM;AB} \right) = OH\).
Vì \(OMBN\) là hình chữ nhật nên \(ON = BM = \dfrac{1}{2}BC = \dfrac{1}{2}.a\sqrt 2 .\sqrt 2 = a\).
Áp dụng hệ thức lượng trong tam giác vuông \(OAN\) ta có: \(OH = \dfrac{{OA.ON}}{{\sqrt {O{A^2} + O{N^2}} }} = \dfrac{{a.a}}{{\sqrt {{a^2} + {a^2}} }} = \dfrac{{a\sqrt 2 }}{2}\).
Chọn C.
Câu hỏi 20 :
Cho hình tứ diện đều ABCD có cạnh bằng a. Gọi M là trung điểm của cạnh AD (tham khảo hình
vẽ dưới). Tính khoảng cách giữa hai đường thẳng AB và CM theo a
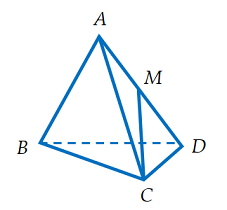
- A \(\dfrac{{a\sqrt {33} }}{{11}}\).
- B \(\dfrac{a}{{\sqrt {33} }}\).
- C \(\dfrac{a}{{\sqrt {22} }}\).
- D \(\dfrac{{a\sqrt {22} }}{{11}}\).
Đáp án: D
Phương pháp giải:
\(\left\{ \begin{array}{l}a//\left( P \right)\\b \subset \left( P \right)\end{array} \right. \Rightarrow d\left( {a;b} \right) = d\left( {a;\left( P \right)} \right)\)
Lời giải chi tiết:
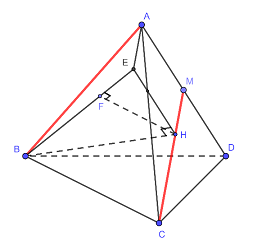
Gọi H là tâm của tam giác đều ACD \( \Rightarrow BH \bot \left( {ACD} \right)\)
Dựng hình chữ nhật AMHE (như hình vẽ). Kẻ HF vuông góc BE.
Do \(CM//AE \subset \left( {ABE} \right) \Rightarrow CM//\left( {ABE} \right) \Rightarrow d\left( {CM;AB} \right) = d\left( {CM;\left( {ABE} \right)} \right) = d\left( {H;\left( {ABE} \right)} \right) = HF\)
Thật vậy:
Ta có: \(\left\{ \begin{array}{l}CM \bot HE\,\,\left( {do\,\,HE//AD} \right)\\CM \bot BH\,\,\left( {do\,\,BH \bot \left( {ACD} \right)} \right)\end{array} \right. \Rightarrow CM \bot \left( {BEH} \right) \Rightarrow CM \bot HF \Rightarrow AE \bot HF\).
Mà \(BE \bot HF \Rightarrow HF \bot \left( {ABE} \right) \Rightarrow d\left( {H;\left( {ABE} \right)} \right) = HF\).
Ta có: \(HE = AM = \dfrac{a}{2}\), \(BH = \sqrt {B{C^2} - C{H^2}} = \sqrt {{a^2} - {{\left( {\dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{3}\)
Ta có: \(\dfrac{1}{{H{F^2}}} = \dfrac{1}{{H{E^2}}} + \dfrac{1}{{B{H^2}}} = \dfrac{1}{{{{\left( {\dfrac{a}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 6 }}{3}} \right)}^2}}} \Rightarrow HF = \dfrac{{a\sqrt {22} }}{{11}}\)\( \Rightarrow d\left( {CM;AB} \right) = \dfrac{{a\sqrt {22} }}{{11}}\).
Chọn D.
Câu hỏi 21 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B;\)\(AB = BC = 1\), \(AD = 2\). Các mặt chéo \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\) cùng vuông góc với mặt đáy \(\left( {ABCD} \right)\). Biết góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {ABCD} \right)\) bằng \({60^0}\) (tham khảo hình vẽ bên). Khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\) là
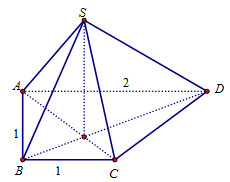
- A \(\dfrac{{2\sqrt 3 }}{3}\)
- B \(\sqrt 3 \).
- C \(2\sqrt 3 \).
- D \(\dfrac{{\sqrt 3 }}{3}\).
Đáp án: B
Lời giải chi tiết:
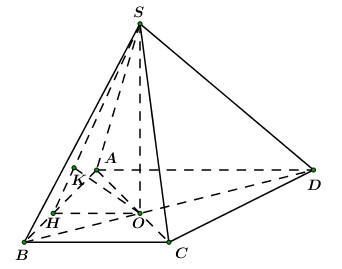
Gọi O là giao điểm của AC và BD.
\( \Rightarrow SO \bot \left( {ABCD} \right).\)
Qua O, kẻ đường thẳng vuông góc với AB, cắt AB tại H.
Ta có: \(\left\{ \begin{array}{l}OH \bot AB\\SO \bot AB\end{array} \right. \Rightarrow AB \bot \left( {SAB} \right) \Rightarrow SH \bot AB.\)
\( \Rightarrow \angle \left( {\left( {SAB} \right),\,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SH,\,\,HO} \right) = \angle SHO = {60^0}.\)
Ta có: \(BC//AD,\) áp dụng định lý Ta-let ta có:
\(\begin{array}{l}\frac{{OA}}{{OC}} = \frac{{OD}}{{OB}} = \frac{{AD}}{{BC}} = 2\\ \Rightarrow \left\{ \begin{array}{l}OA = 2OC\\OD = 2OB\end{array} \right.\end{array}\)
Lại có:\(OA + OC = \sqrt 2 \) \( \Rightarrow \frac{3}{2}OA = \sqrt 2 \Rightarrow OA = \frac{{2\sqrt 2 }}{3}.\)
\( \Rightarrow AH = OH = \frac{{OA}}{{\sqrt 2 }} = \frac{2}{3}.\)
\( \Rightarrow SO = OH.\tan {60^0} = \frac{{2\sqrt 3 }}{3}.\)
Ta có: \(\frac{{DB}}{{OB}} = \frac{{d\left( {D;\,\,\left( {SAB} \right)} \right)}}{{d\left( {O;\,\,\left( {SAB} \right)} \right)}} = 3\) \( \Rightarrow d\left( {D;\,\,\left( {SAB} \right)} \right) = 3d\left( {O;\,\,\left( {SAB} \right)} \right).\)
Từ O dựng đường thẳng vuông góc với SH tại K.
\( \Rightarrow OK \bot \left( {SAB} \right) \Rightarrow d\left( {O;\,\,\left( {SAB} \right)} \right) = OK.\)
Áp dụng hệ thức lượng trong tam giác SOH vuông tại O có đường cao OK ta có:
\(\begin{array}{l}OK = \frac{{OH.SO}}{{\sqrt {O{H^2} + S{O^2}} }} = \frac{{\frac{2}{3}.\frac{{2\sqrt 3 }}{3}}}{{\sqrt {\frac{4}{9} + \frac{4}{3}} }} = \frac{{\frac{{4\sqrt 3 }}{9}}}{{\frac{4}{3}}} = \frac{{\sqrt 3 }}{3}.\\ \Rightarrow d\left( {D;\,\,\left( {SAB} \right)} \right) = \sqrt 3 .\end{array}\)
Chọn B.
Câu hỏi 22 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(B\) và \(C\), \(AB = 2BC = 4CD = 2a\), giả sử \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(BC\). Hai mặt phẳng \(\left( {SMN} \right)\)và \(\left( {SBD} \right)\) cùng vuông góc với mặt phẳng đáy, và cạnh bên \(SB\) hợp với \(\left( {ABCD} \right)\) một góc \({60^0}\). Khoảng cách giữa \(SN\) và \(BD\) là:
- A \(\dfrac{{\sqrt {45} a}}{{15}}\)
- B \(\dfrac{{\sqrt {195} a}}{{65}}\)
- C \(\dfrac{{\sqrt {165} a}}{{55}}\)
- D \(\dfrac{{\sqrt {105} a}}{{35}}\)
Đáp án: B
Phương pháp giải:
- Gọi \(H\) là giao điểm của \(MN\) và \(BD\). Chứng minh \(SH \bot \left( {ABCD} \right)\).
- Xác định góc giữa \(SB\) và mặt đáy là góc giữa \(SB\) và hình chiếu của \(SB\) lên mặt đáy.
- Chứng minh \(BD \bot MN\) bằng cách chứng minh \(\overrightarrow {BD} .\overrightarrow {MN} = 0\).
- Chứng minh \(BD \bot \left( {SMN} \right)\), từ đó dựng đoạn vuông góc chung của \(\) và \(BD\).
- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
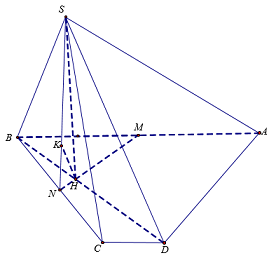
Gọi \(H\) là giao điểm của \(MN\) và \(BD\).
Ta có \(\left\{ \begin{array}{l}SH = \left( {SMN} \right) \cap \left( {SBD} \right)\\\left( {SMN} \right) \bot \left( {ABCD} \right)\\\left( {SBD} \right) \bot \left( {ABCD} \right)\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right)\).
Ta có \(SH \bot \left( {ABCD} \right) \Rightarrow \) \(BH\) là hình chiếu của \(SB\) lên \(\left( {ABCD} \right)\) nên \(\angle \left( {SB;\left( {ABCD} \right)} \right) = \angle \left( {SB;HB} \right)\)\( = \angle SBH = {60^0}\).
Từ giả thiết có \(BC = a\,,\,\,AB = 2a\,,\,\,CD = \dfrac{a}{2}\).
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên \(MN = \dfrac{1}{2}AC\).
Xét \(\overrightarrow {MN} .\overrightarrow {BD} = \dfrac{1}{2}\overrightarrow {AC} .\overrightarrow {BD} \)
\(\begin{array}{l} = \dfrac{1}{2}\left( {\overrightarrow {BC} - \overrightarrow {BA} } \right).\left( {\overrightarrow {BC} + \overrightarrow {CD} } \right)\\ = \dfrac{1}{2}B{C^2} + \dfrac{1}{2}\underbrace {\overrightarrow {BC} .\overrightarrow {CD} }_0 - \dfrac{1}{2}\underbrace {\overrightarrow {BA} .\overrightarrow {BC} }_0 - \dfrac{1}{2}\overrightarrow {BA} .\overrightarrow {CD} \\ = \dfrac{1}{2}.{a^2} - \dfrac{1}{2}.BA.CD.\cos 0\\ = \dfrac{{{a^2}}}{2} - \dfrac{1}{2}.2a.\dfrac{a}{2} = 0\end{array}\)
Suy ra \(BD \bot MN\).
Ta có \(\left\{ \begin{array}{l}BD \bot SH\\BD \bot MN\end{array} \right. \Rightarrow BD \bot \left( {SMN} \right)\).
Mà \(BD \cap \left( {SMN} \right) = \left\{ H \right\}\) nên trong mặt phẳng \(\left( {SMN} \right)\) gọi \(K\) là hình chiếu của \(H\) lên \(SN\), suy ra .. là đoạn vuông góc chung của \(BD\,,\,\,SN\)\( \Rightarrow d\left( {BD\,,\,SN} \right) = HK\).
Áp dụng hệ thức lượng trong tam giác vuông \(BMN\) có \(\dfrac{1}{{B{H^2}}} = \dfrac{1}{{B{M^2}}} + \dfrac{1}{{B{N^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {\dfrac{a}{2}} \right)}^2}}} = \dfrac{5}{{{a^2}}}\)\( \Rightarrow BH = \dfrac{a}{{\sqrt 5 }}\).
Trong tam giác vuông \(HBS\) vuông tại \(H\) có: \(SH = HB.tan{60^0} = \dfrac{{a\sqrt {15} }}{5}\).
Áp dụng định lí Pytago trong tam giác vuông \(HBN\) có \(HN = \sqrt {B{N^2} - H{B^2}} = \sqrt {\dfrac{{{a^2}}}{4} - \dfrac{{{a^2}}}{5}} = \dfrac{{a\sqrt 5 }}{{10}}\).
Áp dụng hệ thức lượng trong tam giác vuông \(HSN\) có
\(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{H{{\rm{S}}^2}}} + \dfrac{1}{{H{N^2}}} = \dfrac{1}{{\dfrac{{3{a^2}}}{5}}} + \dfrac{1}{{\dfrac{{{a^2}}}{{20}}}} = \dfrac{{65}}{{3{a^2}}}\)\( \Rightarrow HK = \dfrac{{a\sqrt {195} }}{{65}}\).
Vậy\(d\left( {BD\,,\,SN} \right) = \dfrac{{a\sqrt {195} }}{{65}}\).
Chọn B.
Câu hỏi 23 :
Hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(SA = SB = SC = a\), \(\angle SAB = {30^0}\), \(\angle SBC = {60^0}\), \(\angle SCA = {45^0}\). Tính khoảng cách d giữa 2 đường thẳng \(AB\) và \(SD\)?
- A \(\dfrac{{4a\sqrt {11} }}{{11}}\)
- B \(\dfrac{{a\sqrt {22} }}{{22}}\)
- C \(\dfrac{{a\sqrt {22} }}{{11}}\)
- D \(\dfrac{{2a\sqrt {22} }}{{11}}\)
Đáp án: C
Phương pháp giải:
- Chuyển tính khoảng cách từ hai đường thẳng chéo nhau sang tính khoảng cách từ điểm đến mặt phẳng.
- Nhận dạng tam giác ABC, tìm vị trí tâm đường tròn ngoại tiếp tam giác này, từ đó suy ra đường cao của hình chóp S.ABCD.
Lời giải chi tiết:
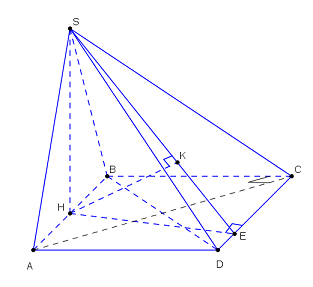
\(\begin{array}{l}S{B^2} = S{A^2} + A{B^2} - 2.SA.AB.\cos {30^0}\\ \Leftrightarrow {a^2} = {a^2} + A{B^2} - 2.a.AB.\dfrac{{\sqrt 3 }}{2}\\ \Leftrightarrow A{B^2} - AB.a\sqrt 3 = 0 \Leftrightarrow AB = a\sqrt 3 \end{array}\)
\(BC = SB = SC = a\) (Tam giác SBC đều)
\(\begin{array}{l}S{A^2} = S{C^2} + A{C^2} - 2.SA.AC.\cos {45^0}\\ \Leftrightarrow {a^2} = {a^2} + A{C^2} - 2.a.AC.\dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow A{C^2} - AC.a\sqrt 2 = 0 \Leftrightarrow AC = a\sqrt 2 \end{array}\)
\( \Rightarrow \) Tam giác ABC vuông tại C
Gọi H là tâm đường tròn ngoại tiếp tam giác ABC \( \Rightarrow H\) là trung điểm của AB và \(SH \bot \left( {ABCD} \right)\).
Tam giác SAH vuông tại H \( \Rightarrow SH = SA.\sin \widehat {SAB} = a.\sin {30^0} = \dfrac{a}{2}\)
Kẻ \(HE \bot CD,\,HK \bot SE \Rightarrow HK \bot \left( {SCD} \right)\). Ta có: \(AB\parallel \left( {SCD} \right)\)
\( \Rightarrow d\left( {AB;CD} \right) = d\left( {AB;\left( {SCD} \right)} \right) = d\left( {H;\left( {SCD} \right)} \right) = HK\)
Ta có: \({S_{ABCD}} = 2.{S_{ABC}} = 2.\dfrac{1}{2}.BC.AC = a.a\sqrt 2 = {a^2}\sqrt 2 \)
Lại có: \({S_{ABCD}} = HE.DC = HE.AB = HE.a\sqrt 3 = {a^2}\sqrt 2 \Rightarrow HE = \dfrac{{a\sqrt 6 }}{3}\)
Tam giác SHE vuông tại H, HK là đường cao
\( \Rightarrow \dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{E^2}}} = \dfrac{1}{{{{\left( {\dfrac{a}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 6 }}{3}} \right)}^2}}} = \dfrac{4}{{{a^2}}} + \dfrac{3}{{2{a^2}}} = \dfrac{{11}}{{2{a^2}}}\)
\( \Rightarrow HK = \dfrac{{a\sqrt {22} }}{{11}} \Rightarrow d\left( {AB;SD} \right) = \dfrac{{a\sqrt {22} }}{{11}}\)
Chọn C.
Câu hỏi 24 :
Cho tứ diện \(ABCD\) có \(\angle ABC = \angle ADC = \angle BCD = {90^0}\), \(BC = 2a\), \(CD = a\), góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\) bằng \({60^0}\). Tính khoảng cách giữa hai đường thẳng \(AC\) và \(BD\).
- A \(\dfrac{{a\sqrt 6 }}{{\sqrt {31} }}\)
- B \(\dfrac{{2a\sqrt 6 }}{{\sqrt {31} }}\)
- C \(\dfrac{{2a\sqrt 3 }}{{\sqrt {31} }}\)
- D \(\dfrac{{a\sqrt 3 }}{{\sqrt {31} }}\)
Đáp án: C
Phương pháp giải:
- Gọi \(E\) là hình chiếu của \(A\) lên \(\left( {ABC} \right)\), chứng minh \(BCDE\) là hình chữ nhật.
- Gọi \(O = BD \cap CE\) là \(A'\) là trung điểm của \(AE\), chứng minh \(d\left( {AC;BD} \right) = d\left( {E;\left( {A'BD} \right)} \right)\).
- Trong \(\left( {BCDE} \right)\) kẻ \(EH \bot BD\,\,\left( {H \in BD} \right)\), trong \(\left( {OA'E} \right)\) kẻ \(EK \bot A'H\,\,\left( {K \in A'H} \right)\), chứng minh \(EK \bot \left( {A'BD} \right)\).
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
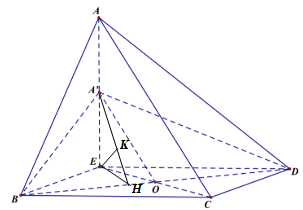
Gọi \(E\) là hình chiếu của \(A\) lên \(\left( {ABC} \right)\) \( \Rightarrow AE \bot \left( {BCD} \right)\).
Ta có: \(\left\{ \begin{array}{l}BC \bot AE\\BC \bot AB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow BC \bot \left( {ABE} \right) \Rightarrow BC \bot BE\).
\(\left\{ \begin{array}{l}CD \bot AE\\CD \bot AD\,\,\left( {gt} \right)\end{array} \right. \Rightarrow CD \bot \left( {AED} \right) \Rightarrow CD \bot DE\).
Do đó \(BCDE\) là hình chữ nhật (Tứ giác có 3 góc vuông).
Ta có \(AE \bot \left( {BCDE} \right) \Rightarrow EB\) là hình chiếu của \(AB\) lên \(\left( {BCDE} \right)\)
\( \Rightarrow \angle \left( {AB;\left( {BCD} \right)} \right) = \angle \left( {AB;EB} \right) = \angle ABE = {60^0}\).
Gọi \(O = BD \cap CE\) là \(A'\) là trung điểm của \(AE\), suy ra \(OA'\parallel AC\) (tính chất đường trung bình).
\( \Rightarrow AC\parallel \left( {A'BD} \right) \supset BD \Rightarrow d\left( {AC;BD} \right) = d\left( {AC;\left( {A'BD} \right)} \right) = d\left( {A;\left( {A'BD} \right)} \right)\).
Lại có \(AE \cap \left( {A'BD} \right) = A' \Rightarrow \dfrac{{d\left( {A;\left( {A'BD} \right)} \right)}}{{d\left( {E;\left( {A'BD} \right)} \right)}} = \dfrac{{AA'}}{{EA'}} = 1\).
\( \Rightarrow d\left( {A;\left( {A'BD} \right)} \right) = d\left( {E;\left( {A'BD} \right)} \right)\).
Trong \(\left( {BCDE} \right)\) kẻ \(EH \bot BD\,\,\left( {H \in BD} \right)\), trong \(\left( {OA'E} \right)\) kẻ \(EK \bot A'H\,\,\left( {K \in A'H} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BD \bot EH\\BD \bot A'E\end{array} \right. \Rightarrow BD \bot \left( {A'HE} \right) \Rightarrow BD \bot EK\\\left\{ \begin{array}{l}EK \bot A'H\\EK \bot BD\end{array} \right. \Rightarrow EK \bot \left( {A'BD} \right) \Rightarrow d\left( {E;\left( {A'BD} \right)} \right) = EK\end{array}\)
Xét tam giác vuông \(ABE\) có: \(AE = BE.\tan {60^0} = a\sqrt 3 \Rightarrow A'E = \dfrac{{a\sqrt 3 }}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(EH = \dfrac{{EB.ED}}{{\sqrt {E{B^2} + E{D^2}} }} = \dfrac{{a.2a}}{{\sqrt {{a^2} + 4{a^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}\)
\(EK = \dfrac{{EA'.EH}}{{\sqrt {EA{'^2} + E{H^2}} }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{{2a}}{{\sqrt 5 }}}}{{\sqrt {\dfrac{{3{a^2}}}{4} + \dfrac{{4{a^2}}}{5}} }} = \dfrac{{2a\sqrt {93} }}{{31}} = \dfrac{{2a\sqrt 3 }}{{\sqrt {31} }}\).
Chọn C.
Câu hỏi 25 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(AB = 3a\), \(AD = DC = a\). Gọi \(I\) là trung điểm của \(AD\), biết hai mặt phẳng \(\left( {SBI} \right)\) và \(\left( {SCI} \right)\) cùng vuông góc với đáy và mặt phẳng \(\left( {SBC} \right)\) tạo với đáy một góc \({60^0}\). Gọi \(M\) điểm trên \(AB\) sao cho \(AM = 2a\), tính khoảng cách giữa \(MD\) và \(SC\).
- A \(\dfrac{{a\sqrt {17} }}{5}\)
- B \(\dfrac{{a\sqrt {15} }}{{10}}\)
- C \(\dfrac{{a\sqrt 6 }}{{19}}\)
- D \(\dfrac{{a\sqrt 3 }}{{15}}\)
Đáp án: B
Phương pháp giải:
- Trong \(\left( {ABCD} \right)\) kéo dài \(AD\) cắt \(BC\) tại \(E\). Sử dụng định lí Ta-lét đảo chứng minh \(MD\parallel BE\).
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng song song và chứa đường thẳng kia.
- Đổi về tính khoảng cách từ \(I\) đến \(\left( {SBE} \right)\).
- Trong \(\left( {SBE} \right)\) kẻ \(IH \bot BE\,\,\left( {H \in BE} \right)\), trong \(\left( {SIH} \right)\) kẻ \(IK \bot SH\,\,\left( {K \in SH} \right)\), chứng minh \(IK \bot \left( {SBE} \right)\).
- Xác định góc giữa \(\left( {SBC} \right)\) và \(\left( {ABCD} \right)\) là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
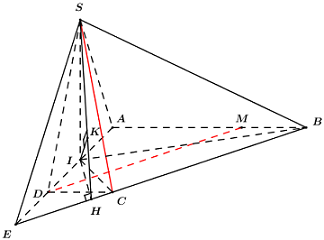
Trong \(\left( {ABCD} \right)\) kéo dài \(AD\) cắt \(BC\) tại \(E\), áp dụng định lí Ta-lét ta có: \(\dfrac{{ED}}{{EA}} = \dfrac{{CD}}{{AB}} = \dfrac{a}{{3a}} = \dfrac{{BM}}{{BA}}\).
\( \Rightarrow MD\parallel BE\) (định lí Ta-lét đảo) \( \Rightarrow MD\parallel \left( {SBE} \right) \supset SC\) \( \Rightarrow d\left( {MD;SC} \right) = d\left( {MD;\left( {SBE} \right)} \right) = d\left( {D;\left( {SBE} \right)} \right)\).
Ta có: \(\left\{ \begin{array}{l}\left( {SBI} \right) \cap \left( {SCI} \right) = SI\\\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\).
Lại có \(DI \cap \left( {SBE} \right) = E\) \( \Rightarrow \dfrac{{d\left( {D;\left( {SBE} \right)} \right)}}{{d\left( {I;\left( {SBE} \right)} \right)}} = \dfrac{{DE}}{{IE}}\).
Ta có: \(\dfrac{{ED}}{{EA}} = \dfrac{{CD}}{{AB}} = \dfrac{1}{3} \Rightarrow \dfrac{{ED}}{{DA}} = \dfrac{1}{2}\) \( \Rightarrow ED = \dfrac{1}{2}AD = \dfrac{a}{2}\), \(IE = ED + DI = \dfrac{a}{2} + \dfrac{a}{2} = a\).
\( \Rightarrow \dfrac{{DE}}{{IE}} = \dfrac{1}{2} \Rightarrow d\left( {D;\left( {SBE} \right)} \right) = \dfrac{1}{2}d\left( {I;\left( {SBE} \right)} \right)\).
Trong \(\left( {SBE} \right)\) kẻ \(IH \bot BE\,\,\left( {H \in BE} \right)\), trong \(\left( {SIH} \right)\) kẻ \(IK \bot SH\,\,\left( {K \in SH} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BE \bot IH\\BE \bot SI\end{array} \right. \Rightarrow BE \bot \left( {SIH} \right) \Rightarrow BE \bot IK\\\left\{ \begin{array}{l}IK \bot BE\\IK \bot SH\end{array} \right. \Rightarrow IK \bot \left( {SBE} \right)\\ \Rightarrow d\left( {I;\left( {SBE} \right)} \right) = IK\end{array}\)
Ta có: \(BE \bot \left( {SIH} \right) \Rightarrow BE \bot SH\).
\(\left\{ \begin{array}{l}\left( {SBE} \right) \cap \left( {ABCD} \right) = BE\\SH \subset \left( {SBE} \right),\,\,SH \bot BE\\IH \subset \left( {ABCD} \right),\,\,IH \bot BE\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {\left( {SBE} \right);\left( {ABCD} \right)} \right) = \angle \left( {SH;IH} \right) = \angle SHI = {60^0}\).
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{S_{ABCD}} = \dfrac{{AD.\left( {AB + CD} \right)}}{2} = \dfrac{{a.\left( {3a + a} \right)}}{2} = 2{a^2}\\{S_{CDI}} = \dfrac{1}{2}CD.CI = \dfrac{1}{2}.a.\dfrac{a}{2} = \dfrac{{{a^2}}}{4}\\{S_{ABI}} = \dfrac{1}{2}AB.AI = \dfrac{1}{2}.3a.\dfrac{a}{2} = \dfrac{{3{a^2}}}{4}\end{array} \right.\\ \Rightarrow {S_{IBC}} = {S_{ABCD}} - {S_{CDI}} - {S_{ABI}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2{a^2} - \dfrac{{{a^2}}}{4} - \dfrac{{3{a^2}}}{4} = {a^2}\end{array}\)
\(BC = \sqrt {{{\left( {AB - CD} \right)}^2} + A{D^2}} = \sqrt {4{a^2} + {a^2}} = a\sqrt 5 \).
Mặt khác ta lại có \({S_{IBC}} = \dfrac{1}{2}IH.BC\) \( \Rightarrow IH = \dfrac{{2{S_{IBC}}}}{{BC}} = \dfrac{{2{a^2}}}{{a\sqrt 5 }} = \dfrac{{2a}}{{\sqrt 5 }}\).
Xét tam giác vuông \(IHK\) có: \(IK = IH.\sin {60^0} = \dfrac{{2a}}{{\sqrt 5 }}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt {15} }}{5}\).
Vậy \(d\left( {MD;SC} \right) = \dfrac{1}{2}IK = \dfrac{{a\sqrt {15} }}{{10}}\).
Chọn B.
Câu hỏi 26 :
Trong không gian cho hai đường thẳng chéo nhau d và \(\Delta \) vuông góc với nhau và nhận \(AB=a\) làm đoạn vuông góc chung \(\left( A\in d;\,\,B\in \Delta \right)\) Trên d lấy điểm M, trên \(\Delta \) lấy điểm N sao cho \(AM=2a;\,\,BN=4a\) Gọi I là tâm mặt cầu ngoại tiếp tứ diện \(ABMN\) Khoảng cách giữa hai đường thẳng \(AM\) và \(BI\) là:
- A \(\frac{4a}{\sqrt{17}}\)
- B \(a\)
- C \(\frac{4a}{5}\)
- D \(\frac{2a\sqrt{2}}{3}\)
Đáp án: A
Phương pháp giải:
+) Xác định tâm I.
+) Dựng mặt phẳng chứa BI và song song AM, đưa về bài toán tính khoảng cách từ 1 điểm đến 1 mặt phẳng.
+) Sử dụng công thức tính thể tích để tính khoảng cách từ 1 điểm đến một mặt phẳng.
Lời giải chi tiết:
Ta có \(\left\{ \begin{align}& AM\bot AB \\& AM\bot BN \\\end{align} \right.\Rightarrow AM\bot \left( ABN \right)\)
\(AB\bot \Delta \Rightarrow AB\bot BN\Rightarrow \Delta ABN\) vuông tại B.
Gọi H, I, K lần lượt là trung điểm của AN, MN và AM ta có:
I là tâm đường tròn ngoại tiếp \(\Delta ABN\); \(IH//AM\Rightarrow IH\bot \left( ABN \right)\Rightarrow IA=IB=IN\)
\(IK//AN\Rightarrow IK\bot AM\Rightarrow IA=IM\)
\(\Rightarrow IM=IA=IB=IN\Rightarrow I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABMN\)
Ta có
\(\begin{align} & AM//IH\Rightarrow AM//\left( BHI \right)\supset BI \\ & \Rightarrow d\left( AM;BI \right)=d\left( AM;\left( BHI \right) \right)=d\left( A;\left( BHI \right) \right) \\\end{align}\)
Ta có \({{S}_{\Delta ABH}}=\frac{1}{2}{{S}_{\Delta ABC}}=\frac{1}{2}.\frac{1}{2}.a.4a={{a}^{2}}\)
\(\begin{align} & IH=\frac{1}{2}AM=a\Rightarrow {{V}_{I.ABH}}=\frac{1}{3}IH.{{S}_{\Delta ABH}}=\frac{1}{3}.a.{{a}^{2}}=\frac{{{a}^{3}}}{3} \\ & {{V}_{I.ABH}}=\frac{1}{3}d\left( A;\left( BHI \right) \right).{{S}_{\Delta BHI}}\Rightarrow d\left( A;\left( BHI \right) \right)=\frac{3{{V}_{I.ABH}}}{{{S}_{\Delta BHI}}} \\\end{align}\)
Mà \(IH\bot \left( ABN \right)\Rightarrow IH\bot BH\Rightarrow \Delta BHI\) vuông tại H có \(HI=a;\,\,BH=\frac{1}{2}AN=\frac{1}{2}\sqrt{{{a}^{2}}+16{{a}^{2}}}=\frac{a\sqrt{17}}{2}\)
\(\Rightarrow {{S}_{\Delta BHI}}=\frac{1}{2}.a.\frac{a\sqrt{17}}{2}=\frac{{{a}^{2}}\sqrt{17}}{4}\)
Vậy \(d\left( AM;BI \right)=d\left( A;\left( BHI \right) \right)=\frac{3.\frac{{{a}^{3}}}{3}}{\frac{{{a}^{2}}\sqrt{17}}{4}}=\frac{4a}{\sqrt{17}}\)
Chọn A.
Câu hỏi 27 :
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại A. Biết \(AB = 2a\),\(AC = a,\,\,AA' = 4a\). Gọi M là điểm thuộc cạnh AA’ sao cho \(MA' = 3MA\). Tính khoảng cách giữa hai đường thẳng chéo nhau \(BC\) và \(C'M\).
- A \(\dfrac{{6a}}{7}\).
- B \(\dfrac{{8a}}{7}\).
- C \(\dfrac{{4a}}{3}\).
- D \(\dfrac{{4a}}{7}\).
Đáp án: B
Lời giải chi tiết:
Gọi \(I = B'M \cap BA'\), ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BC//B'C'\\BC \not\subset \left( {MB'C'} \right)\end{array} \right. \Rightarrow BC//\left( {MB'C'} \right)\\ \Rightarrow d\left( {BC;C'M} \right) = d\left( {BC;\left( {MB'C'} \right)} \right) = d\left( {B;\left( {MB'C'} \right)} \right)\end{array}\)
Mà hai tam giác IMA’ và IB’B đồng dạng, nên:
\(\dfrac{{IA'}}{{IB}} = \dfrac{{MA'}}{{BB'}} = \dfrac{3}{4} \Rightarrow IA' = \dfrac{3}{4}IB \Rightarrow d\left( {B;\left( {MB'C'} \right)} \right) = \dfrac{4}{3}d\left( {A';\left( {MB'C'} \right)} \right)\)
Dựng \(A'K \bot B'C'\)tại K, \(A'H \bot MK\) tại H, ta có:
\(\left\{ \begin{array}{l}B'C' \bot A'K\\B'C' \bot MA'\end{array} \right. \Rightarrow B'C' \bot \left( {MA'K} \right) \Rightarrow A'H \bot B'C'\)
Mà \(A'H \bot MK \Rightarrow A'H \bot \left( {MB'C'} \right) \Rightarrow d\left( {A';\left( {MB'C'} \right)} \right) = A'H\)
Xét tam giác A’B’C’ vuông tại A’ có: \(\dfrac{1}{{A'{K^2}}} = \dfrac{1}{{A'B{'^2}}} + \dfrac{1}{{A'C{'^2}}} = \dfrac{1}{{4{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{5}{{4{a^2}}}\)
Xét tam giác MA’K vuông tại A’ có: \(\dfrac{1}{{A'{H^2}}} = \dfrac{1}{{A'{K^2}}} + \dfrac{1}{{A'{M^2}}} = \dfrac{5}{{4{a^2}}} + \dfrac{1}{{9{a^2}}} = \dfrac{{49}}{{36{a^2}}} \Rightarrow A'H = \dfrac{{6a}}{7}\)
Vậy \(d\left( {BC;C'M} \right) = \dfrac{4}{3}A'H = \dfrac{4}{3}.\dfrac{{6a}}{7} = \dfrac{{8a}}{7}\).
Chọn: B
Câu hỏi 28 :
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh \(2a\) và. Biết góc giữa đường thẳng SA và mặt đáy bằng . Tính khoảng cách từ điểm \(B\) đến mặt phẳng \((SAC)\).
- A \(\dfrac{{\sqrt {15} }}{5}a\)
- B \(\dfrac{{2\sqrt {15} }}{5}a\)
- C \(\dfrac{{2\sqrt {15} }}{3}a\)
- D \(\dfrac{{2\sqrt {51} }}{{15}}a\)
Đáp án: B
Phương pháp giải:
\(d\left( {B;\left( {SAC} \right)} \right) = \dfrac{{3{V_{S.ABC}}}}{{{S_{\Delta SAC}}}}\)
Lời giải chi tiết:
Gọi \(I\) là trung điểm của \(SA\).
Tam giác \(SAB,\,\,SAC\) là các tam giác vuông tại \(B,\,C \Rightarrow IS = IA = IB = IC\).
Gọi \(G\) là trọng tâm tam giác đều \(ABC \Rightarrow IG \bot \left( {ABC} \right)\).
Trong \(\left( {SAG} \right)\) kẻ \(SH//IG\,\,\left( {H \in CG} \right) \Rightarrow SH \bot \left( {ABC} \right)\). Dễ thấy khi đó \(IG\) là đường trung bình của tam giác \(SAH \Rightarrow SH = 2IG\).
Tam giác \(ABC\) đều cạnh \(2a \Rightarrow AG = \dfrac{2}{3}\dfrac{{2a\sqrt 3 }}{2} = \dfrac{{2a\sqrt 3 }}{3}\).
Ta có \(\angle \left( {SA;\left( {ABC} \right)} \right) = \angle \left( {SA;AH} \right) = \angle SAH = {45^0}\).
\( \Rightarrow \Delta AIG\) vuông cân tại \(G \Leftrightarrow IG = AG = \dfrac{{2a\sqrt 3 }}{3} \Rightarrow SH = 2IG = \dfrac{{4a\sqrt 3 }}{3}\).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{4a\sqrt 3 }}{3}\dfrac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = \dfrac{{4{a^3}}}{3}\).
Ta có \(GA = GB = GC\); \(GA = GH\) (\(IG\) là đường trung bình của tam giác \(SAH\))
\( \Rightarrow GA = GB = GC = GH \Rightarrow G\) là tâm đường tròn ngoại tiếp tứ giác \(ABHC\).
\( \Rightarrow AH\) là đường kính đường tròn ngoại tiếp tứ giác \(ABHC\).
\( \Leftrightarrow \angle ACH = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
Ta có: \(AH = 2AG = \dfrac{{4a\sqrt 3 }}{3} \Rightarrow CH = \sqrt {A{H^2} - A{C^2}} = \dfrac{{2a}}{{\sqrt 3 }}\).
\( \Rightarrow SC = \sqrt {S{H^2} + H{C^2}} = \sqrt {{{\left( {\dfrac{{4a\sqrt 3 }}{3}} \right)}^2} + {{\left( {\dfrac{{2a}}{{\sqrt 3 }}} \right)}^2}} = \dfrac{{2\sqrt {15} a}}{3}\).
\({S_{\Delta SAC}} = \dfrac{1}{2}SC.AC = \dfrac{1}{2}.\dfrac{{2\sqrt {15} a}}{3}.2a = \dfrac{{2\sqrt {15} {a^2}}}{3}\).
Vậy \(d\left( {B;\left( {SAC} \right)} \right) = \dfrac{{3{V_{S.ABC}}}}{{{S_{\Delta SAC}}}} = \dfrac{{3.\dfrac{{4{a^3}}}{3}}}{{\dfrac{{2\sqrt {15} {a^2}}}{3}}} = \dfrac{{2a\sqrt {15} }}{5}\).
Chọn B.
Câu hỏi 29 :
Chóp S.ABCD, \(SA\bot \left( ABCD \right),\,\,SA=a,\,\,ABCD\) là hình vuông cạnh a, tâm O. H là hình chiếu vuông góc của A lên SC. Tính \(d\left( H;\left( SBD \right) \right)\).
- A \(\frac{a\sqrt{3}}{7}\)
- B \(\frac{a\sqrt{3}}{8}\)
- C \(\frac{a\sqrt{3}}{9}\)
- D \(\frac{a\sqrt{3}}{10}\)
Đáp án: C
Lời giải chi tiết:
* Đổi khoảng cách từ \(H\to C\) :
\(\frac{SH}{SC}=\frac{S{{A}^{2}}}{S{{C}^{2}}}=\frac{{{a}^{2}}}{3{{a}^{2}}}=\frac{1}{3}\Rightarrow d\left( H;\left( SBD \right) \right)=\frac{1}{3}d\left( C;\left( SBD \right) \right)\,\,\,\left( 1 \right)\).
* Đổi khoảng cách từ \(C\to A\) : Vì OC = OA
\(\Rightarrow d\left( C;\left( SBD \right) \right)=d\left( A;\left( SBD \right) \right)\,\,\,\left( 2 \right)\).
* Từ (1) và (2) \(\Rightarrow d\left( H;\left( SBD \right) \right)=\frac{1}{3}d\left( A;\left( SBD \right) \right)=\frac{1}{3}AK\).
* Tính AK : \(\frac{1}{A{{K}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{O}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{2}{{{a}^{2}}}=\frac{3}{{{a}^{2}}}\Rightarrow AK=\frac{a}{\sqrt{3}}\)
\(\Rightarrow \) Đáp số \(AK=\frac{a}{3\sqrt{3}}=\frac{a\sqrt{3}}{9}\).
Chọn đáp án C.
Câu hỏi 30 :
Lăng trụ \(ABC.A'B'C',\,\,\Delta ABC\) đều, \(AB=a,\,\,A'A=A'B=A'C=a,\,\,M,N\) là trung điểm của BC và A’B. Tính \(d\left( C;\left( AMN \right) \right)\) bằng phương pháp đổi đỉnh.
- A \(\frac{a\sqrt{22}}{11}\)
- B \(\frac{a\sqrt{11}}{22}\)
- C \(\frac{a\sqrt{11}}{11}\)
- D \(\frac{a\sqrt{22}}{22}\)
Đáp án: A
Lời giải chi tiết:
* Nhận xét: Chóp A’.ABC đều. Vẽ O là tâm \(\Delta ABC\Rightarrow A'O\bot \left( ABC \right)\).
* \(AO=\frac{2}{3}AM=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\)
* Tam giác vuông A’OA: \(A'O=\sqrt{{{a}^{2}}-\frac{3{{a}^{2}}}{9}}=\frac{a\sqrt{6}}{3}\)
* \(d\left( N;\left( ABC \right) \right)=\frac{1}{2}A'O=\frac{a\sqrt{6}}{6}\).
* \({{V}_{NACM}}=\frac{1}{3}\left[ d\left( N;\left( ABC \right) \right) \right].{{S}_{\Delta AMC}}=\frac{1}{3}.\frac{a\sqrt{6}}{6}.\frac{1}{2}.\frac{a}{2}.\frac{a\sqrt{3}}{2}=\frac{{{a}^{3}}\sqrt{2}}{48}\)
* \(\Delta A'AB\) đều \(\Rightarrow AN=\frac{a\sqrt{3}}{2}=AM,\,\,MN=\frac{A'C}{2}=\frac{a}{2}\).
Vẽ \(AE\bot MN,\,\,AE=\sqrt{\frac{3{{a}^{2}}}{4}-\frac{{{a}^{2}}}{16}}=\frac{a\sqrt{11}}{4}\)
\(\Rightarrow {{S}_{\Delta AMN}}=\frac{1}{2}.\frac{a}{2}.\frac{a\sqrt{11}}{4}=\frac{{{a}^{2}}\sqrt{11}}{16}\)
* \(d\left( C;\left( AMN \right) \right)=\frac{3{{V}_{NACM}}}{{{S}_{\Delta AMN}}}=\frac{a\sqrt{22}}{11}\)
Chọn đáp án A.
Tổng hợp các bài tập trắc nghiệm khoảng cách mức độ thông hiểu có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm khoảng cách mức độ nhận biết có đáp án và lời giải chi tiết
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |