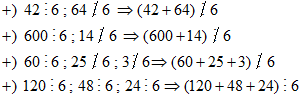Phương pháp giải:

TC2: Nếu chỉ có một số hạng của tổng không chia hết cho một số còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.

Lời giải chi tiết:

 Theo TC2 nếu \(a\) không chia hết cho \(2\) và \(b\) chia hết cho \(2\) thì \(a+b\) không chia hết cho \(2.\)

Chọn B

Phương pháp giải:

Phương pháp: TC1: Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó

Lời giải chi tiết:

Cách giải: Ta có: \(49\vdots 7;\,\,\,70\vdots 7\Rightarrow \left( 49+70 \right)\vdots 7\) (theo TC1)

Chọn A

Phương pháp giải:

Áp dụng tính chất chia hết của một tổng:

Tính chất 1: \(a\,\, \vdots \,\,m\) và \(b\,\, \vdots \,\,m\,\,\,\, \Rightarrow \,\,\,(a + b)\,\, \vdots \,\,m\)

Tính chất 2:  và

Lời giải chi tiết:

Ta có:  \(21\)chia hết cho \(3\);  \(43\) chia cho \(3\) dư \(1\) ;  \(2012\)chia cho \(3\) dư \(2\). Từ đó suy ra \(21 + 43 + 2012\) chia hết cho \(3\).

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Chọn B

Phương pháp giải:

Phương pháp: TC1: Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó

Lời giải chi tiết:

Cách giải: Ta có: \(x\,\,\vdots \,\,2;\,\,y\,\,\vdots \,\,4\Rightarrow y\,\,\vdots \,\,2\Rightarrow \left( x+y \right)\,\,\vdots \,\,2\)

 Chọn A.

Phương pháp giải:

Phương pháp: Nếu số hạng của một hiệu đều chia hết cho cùng một số thì hiệu chia hết cho số đó

Lời giải chi tiết:

Cách giải: Ta có: \(\left\{ \begin{align}  & x\vdots 12\Rightarrow x\vdots 4 \\ & y\vdots 8\Rightarrow y\vdots 4 \\\end{align} \right.\) . Vì \(x\vdots 4;y\vdots 4\Rightarrow \left( x-y \right)\vdots 4\) .

Chọn C

Phương pháp giải:

Phương pháp:

+ TC1:  Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó

+ TC2: Nếu chỉ có một số hạng của tổng không chia hết cho một số còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.

Lời giải chi tiết:

Cách giải:

a)     Vì \(49\,\,\vdots \,\,7;\,\,105\,\,\vdots \,\,7;\,\,399\,\,\vdots \,\,7\Rightarrow \left( 49+105+399 \right)\,\,\vdots \,\,7\) ( theo tính chất 1)

b)     Vì \(48\vdots 8;120\vdots 8\) mà 84 không chia hết cho 8 nên \(84+48+120\) không chia hết cho 8.

Phương pháp giải:

Sử dụng tính chất nếu tất cả các số hạng của tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

Lời giải chi tiết:

 Vì  \(5\,\, \vdots \,\,5;\,\,15\,\, \vdots \,\,5;\,\,70\,\, \vdots \,\,5;\,\,1995\,\, \vdots \,\,5\) nên  \(A = \left( {5 + 15 + 70 + 1995} \right)\,\, \vdots \,\,5\)

Phương pháp giải:

 Áp dụng tính chất chia hết của một tổng.

Lời giải chi tiết:

Vì \(6\,\,\vdots \,\,3\) và \(9\,\,\vdots \,\,3\) nên nếu \(a\,\,\vdots \,\,6\) thì \(a\,\,\vdots \,\,3\); nếu \(b\,\,\vdots \,\,9\) thì \(b\,\,\vdots \,\,3\).

Vì \(a\,\,\vdots \,\,3\) và \(b\,\,\vdots \,\,3\) nên \((a+b)\,\,\vdots \,\,3\)

Chọn B

Lời giải chi tiết:

+) Đáp án A: 48 và 54 đều chia hết cho 6 nên 48 + 54 chia hết cho 6.

+) Đáp án B: 80, 17 và 9 đều không chia hết cho 6 nên 80 + 17 + 9 không chia hết cho 6.

Chọn B.

Phương pháp giải:

Áp dụng tính chất chia hết của một tổng:

Tính chất 1: \(a\,\, \vdots \,\,m\) và \(b\,\, \vdots \,\,m\,\,\,\, \Rightarrow \,\,\,(a + b)\,\, \vdots \,\,m\)

Tính chất 2: a không chia hết cho m và b chia hết cho m \( \Rightarrow \) (a + b) không chia hết cho m

Lời giải chi tiết:

Ta có:

Vậy trong các tổng đã cho, tổng chia hết cho 6 là 120 + 48 + 24.

Chọn D

Phương pháp giải:

Áp dụng tính chất chia hết của một tổng: nếu \(a\,\, \vdots \,\,m\) và \(b\,\, \vdots \,\,m\)thì \((a + b)\,\, \vdots \,\,m\). 

Lời giải chi tiết:

Vì \(4\,\, \vdots \,\,2\) và \(6\,\, \vdots \,\,2\) nên nếu \(x\,\, \vdots \,\,\,4\) thì \(x\,\, \vdots \,\,2\); nếu \(y\,\, \vdots \,\,6\) thì \(y\,\, \vdots \,\,2\).

Vì \(x\,\, \vdots \,\,2\)và \(y\,\, \vdots \,\,2\)nên \((x + y)\,\, \vdots \,\,2\)

Chọn A

Phương pháp giải:

Áp dụng các dấu hiệu chia hết cho \(3;5\) và \(9\):

+) Các số có chữ số tận cùng là \(0;\,\,5\) thì chia hết cho \(5\).

+) Các số có tổng các chữ số chia hết cho \(3\) thì chia hết cho \(3\).

+) Các số có tổng các chữ số chia hết cho \(9\) thì chia hết cho \(9\).

Lời giải chi tiết:

Các số có chữ số tận cùng là \(0;\,\,5\) thì chia hết cho \(5\). Do đó, trong các số đã cho, số chia hết cho \(5\) là các số \(2015;\,\,1140;\,\,1125\).

Ta sẽ tính tổng các chữ số đã cho.

Số \(2015\) có tổng các chữ số là \(2 + 0 + 1 + 5 = 8\). Vì \(8\) không chia hết cho \(9\) và không chia hết cho \(3\) nên số \(2015\) không chia hết cho cả \(3\) và \(9\).

Số \(1140\) có tổng các chữ số là \(1 + 1 + 4 + 0 = 6\). Vì \(6\) không chia hết cho \(9\) nên số \(1140\) không chia hết cho \(9\) và \(6\) chia hết cho \(3\) nên số \(1140\)  chia hết cho \(3\).

Số \(1125\) có tổng các chữ số là \(1 + 1 + 2 + 5 = 9\). Vì \(9\) chia hết cho cả \(3\) và \(9\) nên số \(1125\) chia hết cho cả \(3\) và \(9\).

Vậy số chia hết cho cả \(3;5\) và \(9\) là \(1125\).

Chọn D.

Phương pháp giải:

- Áp dụng dấu hiệu chia hết của 1 tổng, dấu hiện chia hết cho 3 và cho 5.

Lời giải chi tiết:

\(X = {10^{1000}} + 45.\)

Ta có: \({10^{10000}} = 100...0\,\, \vdots \,\,5;\,\,45\,\, \vdots \,\,5\)

\( \Rightarrow X\,\, \vdots \,\,5\)

Ta lại có: 

\({10^{10000}} = 100000...000\) (có tổng chữ số là 1)\( \Rightarrow {10^{10000}}\not  \vdots 3\) và \(45 \vdots 3(4 + 5 = 9 \vdots 3)\)

Suy ra (I) \(X \vdots 5\)

Vậy kết quả là đáp án A.

Chọn A.

Phương pháp giải:

Phương pháp: Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

Lời giải chi tiết:

Vì \(35\vdots 7;\,\,77\vdots 7\Rightarrow \left( 35+77 \right)\,\,\vdots \,\,7\) nên để \(A\vdots 7\) thì \(\left( 6+x \right)\,\,\vdots \,\,7\Rightarrow \left( 6+1+x-1 \right)\,\,\vdots \,\,7\Leftrightarrow \left( 7+x-1 \right)\,\,\vdots \,\,7\) .

Suy ra x chia 7 dư 1. Vậy x có dạng \(x=7.k+1;k\in \mathbb{N}\).

Chọn C

Phương pháp giải:

Phương pháp: Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó

Lời giải chi tiết:

Cách giải: Vì \(n\vdots n\) nên để \(\left( n+3 \right)\vdots n\) thì \(3\vdots n\) . Từ đó suy ra \(n\in \left\{ 1;3 \right\}\)

Chọn C

Phương pháp giải:

Phương pháp: Nhân \(a+4b\) với 10, biến đổi rồi chứng minh dựa vào TC1:  Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó

Lời giải chi tiết:

Cách giải: Xét \(10.\left( a+4.b \right)=10.a+40.b=\left( 10.a+b \right)+39.b\) .

Vì \(\left( 10.a+b \right)\,\,\vdots \,\,13\) và \(39b\,\,\vdots \,\,13\) nên \(10.\left( a+4.b \right)\,\,\vdots \,\,13\) .

Do 10 không chia hết cho 13 nên suy ra \(\left( a+4.b \right)\,\,\vdots \,\,13\) .

Vậy nếu \(10a+b\) chia hết cho 13 thì \(a+4b\) chia hết cho 13.

Phương pháp giải:

Phương pháp: TC1:  Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó

Lời giải chi tiết:

Cách giải:

a)     Vì \(12\,\,\vdots \,\,3;\,\,15\,\,\vdots \,\,3;\,\,36\,\,\vdots \,\,3\Rightarrow \left( 12+15+36 \right)\,\,\vdots \,\,3\) nên để \(A\,\,\vdots \,\,3\) thì \(x\vdots 3\).

b)     Ta có: \(A=\left( 12+15 \right)+36+x\) . Vì \(12+15=27\,\,\vdots \,\,9\) và \(36\,\,\vdots \,\,9\Rightarrow \left( 12+15+36 \right)=\left( 27+36 \right)\,\,\vdots \,\,9\) nên để A không chia hết cho 9 thì x không chia hết cho 9.

Phương pháp giải:

Phương pháp: TC1:  Nếu số hạng của một hiệu đều chia hết cho cùng một số thì hiệu chia hết cho số đó

Lời giải chi tiết:

Cách giải:

Vì \(\left( n+3 \right)\vdots \left( n+3 \right)\) nên theo tính chất 1 để \(\left( n+8 \right)\vdots \left( n+3 \right)\) thì \(\left[ \left( n+8 \right)-\left( n+3 \right) \right]\vdots \left( n+3 \right)\) hay \(5\vdots \left( n+3 \right)\) .

Suy ra \(\left( n+3 \right)\in \left\{ 1;5 \right\}\) .

Vì \(n+3\ge 3\) nên \(n+3=5\Rightarrow n=5-3=2.\)

Vậy \(n=2.\)

Phương pháp giải:

- Thực hiện phép chia: \(275:8\). Thương tìm được chính là số túi sầu riêng và số dư là số trái sầu riêng còn dư.

- Lấy số túi sầu riêng tìm được ở trên chia cho \(8\). Thương tìm được chính là số thùng carton sầu riêng và số dư là số túi sầu riêng còn dư.

Lời giải chi tiết:

Ta có: \(275:8 = 34\) dư \(3\).

Do đó, gia đình bạn Nguyễn đóng gói được \(34\) túi và còn dư \(3\) trái sầu riêng.

Lại có: \(34:8 = 4\) dư \(2\).

Do đó, gia đình bạn Nguyễn đóng gói được \(4\) thùng carton và còn dư \(3\) túi sầu riêng sầu riêng.

Vậy gia đình bạn Nguyễn cần dùng  \(4\) thùng carton, \(34\) túi và còn dư \(3\) trái sầu riêng.

Chọn B.

Phương pháp giải:

Tổng B có 102 số hạng nên nhóm ba số hạng liền nhau , biến đổi để chứng minh dựa vào tính chất : \(a\vdots m\Rightarrow a.k\vdots m;k\in \mathbb{N}\)

Lời giải chi tiết:

\(B=5+{{5}^{3}}+{{5}^{5}}+...+{{5}^{201}}+{{5}^{203}}\) có 102 số hạng, có \(102\,\,\vdots \,\,3\) .

Ghép ba số hạng của dãy số thành 1 nhóm ta được \(102:3=34\) nhóm như sau:

\(\begin{array}{l}B = 5 + {5^3} + {5^5} + ... + {5^{201}} + {5^{203}}\\\,\,\,\,\, = \left( {5 + {5^3} + {5^5}} \right) + \left( {{5^7} + {5^9} + {5^{11}}} \right) + ... + \left( {{5^{199}} + {5^{201}} + {5^{203}}} \right)\\\,\,\,\,\, = 5.\left( {1 + {5^3} + {5^4}} \right) + {5^7}.\left( {1 + {5^3} + {5^4}} \right) + ... + {5^{199}}.\left( {1 + {5^3} + {5^4}} \right)\\\,\,\,\,\, = 5.651 + {5^7}.651 + ... + {5^{199}}.651\\\,\,\,\,\, = \left( {5 + {5^7} + ... + {5^{199}}} \right).651\\\,\,\,\,\, = \left( {5 + {5^7} + ... + {5^{199}}} \right).21.31\,\, \vdots \,\,31\end{array}\)

Vậy \(B=5+{{5}^{3}}+{{5}^{5}}+...+{{5}^{201}}+{{5}^{203}}\) chia hết cho 31.

Phương pháp giải:

Áp dụng tính chất chia hết của một tổng.

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}\left( {a + 5b} \right)\,\, \vdots \,\,7\,\,\,\,\,(a,\,b \in N)\\ \Rightarrow 10.(a + 5b)\,\, \vdots \,\,7\\ \Rightarrow \left( {10a + 50b} \right)\,\,\, \vdots \,\,7\\ \Rightarrow \left( {10a + b + 49b} \right)\,\,\, \vdots \,\,7\\ \Rightarrow \left[ {(10a + b) + 49b} \right]\,\,\, \vdots \,\,7\end{array}\)

Mà \(49b\,\,\, \vdots \,\,7\) nên suy ra \(\left( {10a + b} \right)\,\,\, \vdots \,\,7\).

Vậy  \(\left( {a + 5b\,} \right)\, \vdots \,\,7\,\,(a,\,b \in N)\) thì \(\left( {10a + b} \right)\,\, \vdots \,\,7.\)

Phương pháp giải:

Sử dụng tính chất chia hết. \(M = \left( {9a + 11b} \right)\left( {5b + 11a} \right) \vdots 19\,\,\,\,\,\left( {a,b \in {N^*}} \right)\) thì nó cũng chia hết cho \(361\) ta cần chỉ ra, một trong hai số chia hết cho \(19\) thì số còn lại cũng chia hết cho \(19.\)

Lưu ý: \(361 = 19 \times 19.\)

Xét: \(m\left( {9a + 11b} \right) + n\left( {5b + 11a} \right) \vdots 19\) với \(m,\, n\) nguyên tố cùng nhau.

Lời giải chi tiết:

Ta có: với \(a,\,\,b \in {\mathbb{N}^*} \Rightarrow 9a + 11b\) và \(5b + 11a\) cùng là các số tự nhiên khác \(0.\)

Khi đó \(M = \left( {9a + 11b} \right)\left( {5b + 11a} \right)\,\, \vdots \,\,19\) thì \(\left[ \begin{array}{l}9a + 11b\,\, \vdots \,\,19\\5b + 11a\,\, \vdots \,\,19\end{array} \right..\)

TH1: Xét \(9a + 11b\,\, \vdots \,\,19\)

\( \Rightarrow \) Để chứng minh \(M\,\, \vdots \,\,361,\) ta cần chứng minh \(5b + 11a\,\, \vdots \,\,19.\)

Ta có: \(38\,\, \vdots \,\,19 \Rightarrow 38\left( {a + b} \right)\,\, \vdots \,\,19\)

\(\begin{array}{l}38\left( {a + b} \right) = 38a + 38b = 11a + 27a + 5b + 33b\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {27a + 33b} \right) + 11a + 5b = 3\left( {9a + 11b} \right) + \left( {11a + 5b} \right).\end{array}\)

Vì \(9a + 11b\,\, \vdots \,\,19 \Rightarrow 3\left( {9a + 11b} \right)\,\, \vdots \,\,19\) và \(38\left( {a + b} \right)\,\,\, \vdots \,\,19\)

  \(\begin{array}{l} \Rightarrow 11a + 5b\,\, \vdots \,\,19.\\ \Rightarrow M = \left( {9a + 11b} \right)\left( {5b + 11a} \right)\,\, \vdots \,\,361.\end{array}\)

TH2: Xét \(5b + 11a\,\, \vdots \,\,19\)

\( \Rightarrow \) Để chứng minh \(M\,\, \vdots \,\,361,\) ta cần chứng minh \(9a + 11b\,\, \vdots \,\,19.\)

Ta có: \(38\,\, \vdots \,\,19 \Rightarrow 38\left( {a + b} \right)\,\, \vdots \,\,19\)

\(\begin{array}{l}38\left( {a + b} \right) = 38a + 38b = 11a + 27a + 5b + 33b\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {27a + 33b} \right) + 11a + 5b = 3\left( {9a + 11b} \right) + \left( {11a + 5b} \right).\end{array}\)

Vì \(38\left( {a + b} \right)\,\, \vdots \,\,19\) và \(11a + 5b\,\,\, \vdots \,\,19\)

\(\begin{array}{l} \Rightarrow 3\left( {9a + 11b} \right)\,\, \vdots \,\,19 \Rightarrow 9a + 11b\,\, \vdots \,\,19.\\ \Rightarrow M = \left( {9a + 11b} \right)\left( {5b + 11a} \right)\,\, \vdots \,\,361.\end{array}\)

Vậy khi \(M = \left( {9a + 11b} \right)\left( {5b + 11a} \right)\,\, \vdots \,\,19\) thì \(M\,\, \vdots \,\,361.\)

Phương pháp giải:

Chứng minh \(a \vdots 2018\) Rồi suy ra \(b \vdots 2018\). Lưu ý : \(a \vdots b \Rightarrow k.a \vdots b\,\,\left( {k \in Z} \right)\)

Lời giải chi tiết:

Ta có :

\(\begin{array}{l}(5a + 3b) \vdots 2018 \Rightarrow 8.(5a + 3b) \vdots 2018\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\left( {13a + 8b} \right) \vdots 2018 \Rightarrow 3.\left( {13a + 8b} \right) \vdots 2018\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\\ \Rightarrow 8.(5a + 3b) - 3.\left( {13a + 8b} \right)\,\,\,\,\,\,\,\,\, \vdots 2018\\ \Rightarrow \,\,\,\,\,\,40a + 24b - 39a - 24b\,\,\,\,\,\,\,\,\,\, \vdots 2018\\ \Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots 2018\end{array}\)

Mà \(5a + 3b \vdots 2018 \Rightarrow \,\,\,\,\,\,3b \vdots 2018\) (trong đó \(\left( {3;\,2018} \right) = 1\))

\( \Rightarrow b \vdots 2018\)

Vậy \(5a + 3b\) và \(13a + 8b\) cùng chia hết cho 2018 thì a và b cũng chia hết cho 2018.

Phương pháp giải:

Viết \(A\) dưới dạng tổng của các nhóm thích hợp.

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}A = 3 + {3^2} + {3^3} + {3^4} + ... + {3^{25}}\\A = 3 + \left( {{3^2} + {3^3} + {3^4} + {3^5}} \right) + \left( {{3^6} + {3^7} + {3^8} + {3^9}} \right) + ... + \left( {{3^{22}} + {3^{23}} + {3^{24}} + {3^{25}}} \right)\\\,\,\,\,\, = 3 + {3^2}.\left( {1 + 3 + {3^2} + {3^3}} \right) + {3^6}.\left( {1 + 3 + {3^2} + {3^3}} \right) + ... + {3^{22}}.\left( {1 + 3 + {3^2} + {3^3}} \right)\\\,\,\,\,\, = 3 + {3^2}.40 + {3^6}.40 + ... + {3^{22}}.40\\\,\,\,\,\, = 3 + 40.\left( {{3^2} + {3^6} + ... + {3^{22}}} \right)\end{array}\).

Mà \(40.\left( {{3^2} + {3^6} + ... + {3^{22}}} \right)\,\, \vdots \,\,40\)

Vậy số dư khi chia \(A\) cho \(40\) là \(3\).

Chọn D.