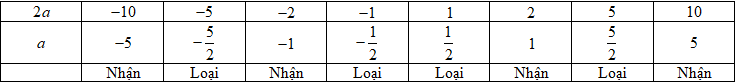20 bài tập tổng hợp Bội và ước của một số nguyên
Làm đề thiCâu hỏi 1 :
Các bội của 5 là:
- A \(-5;\,\ 5;\ \,0;\,\ 23;\,-23\)
- B \(212;\,-212;\ \,15\)
- C \(-1;\,\ 1;\,\ 5;\,-5\)
- D \(0;\ \,5;\,-5;\ \,10;\,-10;\,...\)
Đáp án: D
Phương pháp giải:
Sử dụng khái niệm bội và ước của một số nguyên:
Nếu \(a,b,x\in Z\) và \(a=b.x\) thì \(a\vdots b\)và a là một bội của b; b là một ước của a
Lời giải chi tiết:
Bội của 5 là số 0 và những số nguyên có hàng đơn vị là 0 và 5.
Các bội của 5 là: \(0;\ \,5;\,-5;\,\ 10;\,-10;\,...\)
Chọn D
Câu hỏi 2 :
Tập hợp các ước của -6 là:
- A \(A=\left\{ 1;\,-1;\,\ 2;\,-2;\,\ 3;\,-3;\,\ 6;\,-6 \right\}\)
- B \(A=\left\{ 1;\ \,2;\,\ 3;\ \,6;\,\ 12;\,... \right\}\)
- C \(A=\left\{ 0;\ \,6;\,-6;\,\ 12;\,-12;\,... \right\}\)
- D \(A=\left\{ 16;\,-16;\,\ 26;\,-26;\,... \right\}\)
Đáp án: A
Phương pháp giải:
Sử dụng khái niệm bội và ước của một số nguyên:
Nếu \(a,b,x\in Z\) và \(a=b.x\) thì \(a\vdots b\)và a là một bội của b; b là một ước của a
Lời giải chi tiết:
Ta có: \(-6=-1.6=1.\left( -6 \right)=-2.3=2.\left( -3 \right).\)
Tập hợp các ước của -6 là: \(A=\left\{ 1;\,-1;\ \,2;\,-2;\,\ 3;\,-3;\,\ 6;\,-6 \right\}\)
Chọn A
Câu hỏi 3 :
Cho \(x\in \mathbb{Z}\) và \(\left( -258+x \right)\vdots 3\) thì:
- A x chia 3 dư 1
- B \(x\vdots 3\)
- C x chia 3 dư 2
- D x không chia hết cho 3
Đáp án: B
Phương pháp giải:
Sử dụng tính chất chia hết trong tập hợp các số nguyên: \(a\vdots m;b\vdots m\Rightarrow (a+b)\vdots m\)
Lời giải chi tiết:
Vì \(-258\) có tổng các chữ số là \(2+5+8=15\vdots 3\) nên \(-258\vdots 3\) .
Do đó để \(\left( -258+x \right)\vdots 3\) thì \(x\vdots 3\).
Chọn B
Câu hỏi 4 :
Tìm tất cả các ước chung của -12 và 30
- A \(\left\{ \pm 1;\,\pm 2;\,\pm 4;\,\,\pm 6 \right\}\)
- B \(\left\{ \pm 1;\,\pm 2;\,\pm 3;\,\,\pm 6 \right\}\)
- C \(\left\{ \pm 1;\,\pm 2;\,\pm 3;\,\,\pm 5 \right\}\)
- D \(\left\{ \pm 1;\,\pm 2;\,\pm 3;\,\,\pm 7 \right\}\)
Đáp án: B
Phương pháp giải:
+ Sử dụng khái niệm bội và ước của số nguyên để tìm ước của -12 và ước của 30
+ Sử dụng tính chất sau để tìm ước chung của chúng:
Nếu c vừa là ước của a vừa là ước của b thì c cũng được gọi là ước chung của a và b.
Lời giải chi tiết:
Tập hợp các ước của -12 và 30 là:
\(\begin{align} & U\left( -12 \right)=\left\{ \pm 1;\,\ \pm 2;\ \,\pm 3;\,\ \pm 4;\ \,\pm 6;\ \,\pm 12 \right\} \\ & U\left( 30 \right)=\left\{ \pm 1;\,\ \pm 2;\ \,\pm 3;\,\ \pm 5;\,\ \pm 6;\,\ \pm 10;\,\ \pm 15;\ \,\pm 30 \right\} \\ \end{align}\)
Suy ra tập hợp các ước chung của -12 và 30 là: \(UC\left( -12;\,30 \right)=\left\{ \pm 1;\,\pm 2;\,\pm 3;\,\,\pm 6 \right\}\)
Chọn B
Câu hỏi 5 :
Tập hợp các ước của \( - 8\) là:
- A \(\left\{ \pm 1;\pm 2;\pm 4 \right\}\)
- B \(\left\{ \pm 1;\pm 2;\pm 4;\pm 8 \right\}\)
- C \(\left\{ \pm 2;\pm 4;\pm 8 \right\}\)
- D \(\left\{ \pm 1;\pm 4;\pm 8 \right\}\)
Đáp án: B
Phương pháp giải:
Áp dụng định nghĩa ước của một số: Nếu \(a \vdots b\) thì b là ước của a.
Lời giải chi tiết:
\(U(8)= \left\{ { \pm 1; \pm 2; \pm 4; \pm 8} \right\}\)
Chọn B.
Câu hỏi 6 :
Tìm tất cả các ước chung của \( - 24\) và \(30\).
- A \(\left\{ { \pm 1; \pm 2; \pm 3; \pm 6} \right\}\)
- B \(\left\{ { \pm 1; \pm 2; \pm 3; \pm 4 \pm 6} \right\}\)
- C \(\left\{ { \pm 1; \pm 2; \pm 3; \pm 4} \right\}\)
- D \(\left\{ { \pm 1; \pm 2; \pm 4; \pm 6} \right\}\)
Đáp án: A
Phương pháp giải:
Xác định ước chung thông qua UCLN (Đưa về số nguyên dương)
Lời giải chi tiết:
Ước chung của \( - 24\) và \(30\) là ước của \(UCLN\left( {24;\,\,30} \right) = 6\).
\( \Rightarrow UC\left( { - 24;30} \right) = U\left( 6 \right) = \left\{ { \pm 1;\,\, \pm 2;\,\, \pm 3;\,\, \pm 6} \right\}\)
Chọn A.
Câu hỏi 7 :
Tìm các số nguyên \(a\), biết:
Câu 1:
\(a + 2\) là ước của \(7.\)
- A \(a \in \left\{ { - 7; - 1;1;7} \right\}\)
- B \(a \in \left\{ { - 9; - 3; - 1;5} \right\}\)
- C \(a \in \left\{ { - 7; - 3; - 1;5} \right\}\)
- D \(a \in \left\{ { - 3; - 1;1;5} \right\}\)
Đáp án: B
Phương pháp giải:
+) Liệt kê để tìm được ước của các số.
Lời giải chi tiết:
Theo bài ra có, \(a + 2 \in U\left( 7 \right) = \left\{ { \pm 1; \pm 7} \right\}\). Ta có bảng sau:
Vậy \(a \in \left\{ { - 9; - 3; - 1;5} \right\}\).
Chọn B.
Câu 2:
\(2a\) là ước của \( - 10.\)
- A \(a \in \left\{ { - 10; - 2;2;10} \right\}.\)
- B \(a \in \left\{ { - 5; - 2;2;5} \right\}.\)
- C \(a \in \left\{ { - 10; - 2;2;10} \right\}.\)
- D \(a \in \left\{ { - 5; - 1;1;5} \right\}.\)
Đáp án: D
Phương pháp giải:
+) Liệt kê để tìm được ước của các số.
Lời giải chi tiết:
Theo bài ra có \(2a \in U\left( { - 10} \right) = \left\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\). Ta có bảng sau:
Vậy \(a \in \left\{ { - 5; - 1;1;5} \right\}.\)
Chọn D.
Câu hỏi 8 :
Cho \(x\in \mathbb{Z}\) và \(x+9\) là ước của 7 thì:
- A \(x=-2;\,-8\)
- B \(x=-8;\,-10;\,-2;\,-16\)
- C \(x=10;\,\ 8;\,\ 17;\ \,3\)
- D \(x=1;\,-1;\,\ 7;\,-7\)
Đáp án: B
Phương pháp giải:
+ Sử dụng khái niệm bội và ước của một số nguyên để tìm các ước của 7
+ Lập bảng giá trị để tìm x
Lời giải chi tiết:
Ta có:\(\left( x+9 \right)\in U\left( 7 \right)\Rightarrow \left( x+9 \right)\in \left\{ -7;\,-1;\,7;\,1 \right\}\)
Xét bảng:
Vậy \(x\in \left\{ -16;\,-10;\,-8;\,-2 \right\}\) .
Chọn B
Câu hỏi 9 :
Cho \(x,\,y\in \mathbb{Z}\) và \(x.y=-3\) thì các cặp giá trị \(\left( x;\,y \right)\) là:
- A \(\left( 1;\,-3 \right);\,\left( -3;\,1 \right)\)
- B \(\left( -1;\,3 \right);\,\left( 3;\,-1 \right)\)
- C \(\left( 1;-3 \right);\,\left( -3;\,1 \right);\,\left( -1;\,3 \right);\,\left( 3;\,-1 \right)\)
- D \(\left( 3;\,-1 \right);\,\left( 1;\,-3 \right)\)
Đáp án: C
Phương pháp giải:
+ Sử dụng khái niệm bội và ước của một số nguyên để tìm các ước của -3
+ Lập bảng giá trị để tìm cặp giá trị \(\left( x;\,y \right)\)
Lời giải chi tiết:
Ta có: \(x.y=-3\)
Mà \(x,\,y\in \mathbb{Z}\) nên \(x;\,y\in U\left( -3 \right)=\left\{ -3;\,-1;\,\ 1;\,\ 3 \right\}\) .
Xét bảng:
Vậy ta có các cặp giá trị \(\left( x;\,y \right)\) là: \(\left( 1;-3 \right);\,\left( -3;\,1 \right);\,\left( -1;\,3 \right);\,\left( 3;\,-1 \right)\)
Chọn C
Câu hỏi 10 :
Chứng minh rằng nếu a là bội của b thì:
a) \(-a\) là bội của b
b) \(-b\) là ước của a
Phương pháp giải:
Sử dụng khái niệm bội và ước của một số nguyên để chứng minh:
Nếu \(a,b,x\in Z\) và \(a=b.x\) thì \(a\vdots b\) và a là một bội của b; b là một ước của a
Lời giải chi tiết:
a) Vì a là bội của b nên \(a=b.x,\,\left( x\in \mathbb{Z} \right)\) .
Suy ra \(-a=-\left( b.x \right)=b.\left( -x \right)\) .
Mà \(x\in \mathbb{Z}\) suy ra \(-x\in \mathbb{Z}\) , suy ra \(\left( -a \right)\vdots b\) hay \(-a\) là bội của b.
b) Vì b là ước của a nên \(a=b.x,\,\left( x\in \mathbb{Z} \right)\).
Suy ra \(a=\left( -b \right).\left( -x \right)\) .
Mà \(x\in \mathbb{Z}\) suy ra \(-x\in \mathbb{Z}\) , suy ra \(a\vdots \left( -b \right)\) hay –b là ước của a.
Câu hỏi 11 :
Tìm \(x;\,y\in \mathbb{Z}\) sao cho:
a) \(x-5\) là bội của \(x+2\)
b) \(\left( 2x+1 \right)\left( y-3 \right)=-10\)
- A a) \(x\in \left\{ -9;\,-3;\,-1;\,5 \right\}\)
b) \(\left( -1;\,13 \right);\left( 0;\,-7 \right);\left( 3;\,5 \right);\left( 12;\,1 \right)\)
- B a) \(x\in \left\{ -9;\,-3;\,-1;\,5 \right\}\)
b) \(\left( -1;\,3 \right);\left( 0;\,-7 \right);\left( -3;\,5 \right);\left( 2;\,1 \right)\)
- C a) \(x\in \left\{ -9;\,-3;\,-2;\,5 \right\}\)
b) \(\left( -1;\,13 \right);\left( 0;\,-7 \right);\left( -3;\,5 \right);\left( 2;\,1 \right)\)
- D a) \(x\in \left\{ -9;\,-3;\,-1;\,5 \right\}\)
b) \(\left( -1;\,13 \right);\left( 0;\,-7 \right);\left( -3;\,5 \right);\left( 2;\,1 \right)\)
Đáp án: D
Phương pháp giải:
a) + Tách \(x-5=\left( x+2 \right)-7\), sử dụng tính chất chia hết của một tổng suy ra x+2 thuộc ước của 7
+ Tìm ước của 7 rồi lập bảng ta tính được giá trị của x
b) + Sử dụng khái niệm bội và ước của số nguyên để suy ra 2x+1 và y-3 là ước của -10
+ Tìm ước của -10
+ Sử dụng tính chất chia hết để loại bớt các trường hợp
+ Lập bảng giá trị để tìm các cặp giá trị \(\left( x;\,y \right)\)
Lời giải chi tiết:
a) \(x-5\) là bội của \(x+2\)
Ta có: \(\left( x+2 \right)\ \vdots \ \left( x+2 \right).\)
Lại có: \(x-5=\left( x+2 \right)-7\)
\(\begin{align} & \Rightarrow \left( x-5 \right)\ \vdots \ \left( x+2 \right)\Leftrightarrow 7\ \vdots \ \left( x+2 \right). \\ & \Rightarrow \left( x+2 \right)\in \ U\left( 7 \right)\Leftrightarrow \left( x+2 \right)\in \left\{ \pm 1;\ \pm 7 \right\}. \\ \end{align}\)
Ta có bảng sau:
Vậy \(x\in \left\{ -9;\,-3;\,-1;\,5 \right\}\)
b)\(\left( 2x+1 \right)\left( y-3 \right)=-10\)
Vì \(x;\,y\in \mathbb{Z}\Rightarrow \left( 2x+1 \right);\,\left( y-3 \right)\in \mathbb{Z}\) mà \(\left( 2x+1 \right)\left( y-3 \right)=-10\)
\(\Rightarrow \left( 2x+1 \right);\left( y-3 \right)\in U\left( -10 \right)\)
Mà \(U\left( -10 \right)=\left\{ \pm 1;\ \pm 2;\,\pm 5;\,\pm 10 \right\}\)
Ta có: \(2x\ \vdots \ 2\Rightarrow \left( 2x+1 \right)\ \) không chia hết cho \(2\Rightarrow \left( 2x+1 \right)\in \left\{ \pm 1;\ \pm 5 \right\}.\)
Ta có bảng:

Vậy ta có các cặp giá trị \(\left( x;\,y \right)\) là: \(\left( -1;\,13 \right);\left( 0;\,-7 \right);\left( -3;\,5 \right);\left( 2;\,1 \right)\)
Chọn D
Câu hỏi 12 :
Cho x là số nguyên và \(x+1\) là ước của 5 thì giá trị của x là:
- A \(0;\,-2;\,\ 4;\,-6\)
- B \(0;\,-2;\ \,4;\ \,6\)
- C \(0;\,\ 1;\ \,3;\,\ 6\)
- D \(2;\,-4;\,-6;\,\ 7\)
Đáp án: A
Phương pháp giải:
+ Sử dụng khái niệm bội và ước của một số nguyên để tìm các ước của 5.
+ Lập bảng giá trị để tìm x.
Lời giải chi tiết:
Ta có: \(\left( x+1 \right)\in U\left( 5 \right)\Rightarrow \left( x+1 \right)\in \left\{ -5;\,-1;\ \,1;\,\ 5 \right\}.\)
Xét bảng:
Vậy \(x\in \left\{ 0;\,4;\,-2;\,-6 \right\}\) .
Chọn A
Câu hỏi 13 :
Chứng minh rằng nếu \(a \in \mathbb{Z}\) thì:
a) \(M = a\left( {a + 2} \right) - a\left( {a - 5} \right) - 7\) là bội của \(7.\)
b) \(N = \left( {a - 2} \right)\left( {a + 3} \right) - \left( {a - 3} \right)\left( {a + 2} \right)\) là số chẵn.
Phương pháp giải:
Ta thực hiện theo 2 bước sau:
Bước 1: Rút gọn biểu thức
Bước 2: Áp dụng \(a \vdots b \Rightarrow ka \vdots b\,\)(với \(\forall k \in \mathbb{Z}\))
Lời giải chi tiết:
a) Với \(a \in \mathbb{Z}\) ta có:
\(M = a\left( {a + 2} \right) - a\left( {a - 5} \right) - 7\)
\(\,\,\,\,\,\,\, = \left( {a.a + a.2} \right) - \left( {a.a - a.5} \right) - 7\)
\(\,\,\,\,\,\,\, = \left( {{a^2} + 2a} \right) - \left( {{a^2} - 5a} \right) - 7\)
\(\,\,\,\,\,\,\, = {a^2} + 2a - {a^2} + 5a - 7\)
\(\,\,\,\,\,\,\, = \left( {{a^2} - {a^2}} \right) + \left( {2a + 5a} \right) - 7\)
\(\,\,\,\,\,\,\, = 7a - 7\)
\(\,\,\,\,\,\,\, = 7\left( {a - 1} \right)\)
Vì \(7 \vdots 7 \Rightarrow 7\left( {a - 1} \right) \vdots 7 \Rightarrow M \vdots 7 \Rightarrow M\)là bội của \(7\).
b) Để chứng minh \(N = \left( {a - 2} \right)\left( {a + 3} \right) - \left( {a - 3} \right)\left( {a + 2} \right)\) là số chẵn, ta chứng minh \(N \vdots 2\) với \(a \in \mathbb{Z}\).
\(N = \left( {a - 2} \right)\left( {a + 3} \right) - \left( {a - 3} \right)\left( {a + 2} \right)\)
\(\,\,\,\,\,\, = \left[ {a\left( {a + 3} \right) - 2\left( {a + 3} \right)} \right] - \left[ {a\left( {a + 2} \right) - 3\left( {a + 2} \right)} \right]\)
\(\,\,\,\,\,\, = \left[ {\left( {{a^2} + 3a} \right) - \left( {2a + 6} \right)} \right] - \left[ {\left( {{a^2} + 2a} \right) - \left( {3a + 6} \right)} \right]\)
\(\,\,\,\,\,\, = \left( {{a^2} + 3a - 2a - 6} \right) - \left( {{a^2} + 2a - 3a - 6} \right)\)
\(\,\,\,\,\,\, = {a^2} + 3a - 2a - 6 - {a^2} - 2a + 3a + 6\)
\(\,\,\,\,\,\, = \left( {{a^2} - {a^2}} \right) + \left( {3a - 2a - 2a + 3a} \right) + \left( {6 - 6} \right)\)
\(\,\,\,\,\,\, = 2a\)
Vì \(2 \vdots 2 \Rightarrow 2a \vdots 2 \Rightarrow N \vdots 2\) suy ra \(N\) là số chẵn.
Câu hỏi 14 :
Tìm \(x \in \mathbb{Z}\) sao cho:
Câu 1:
\({x^2} + 2\) là bội của \(x + 2.\)
- A \(x \in \left\{ { - 8;\,\, - 5;\,\, - 4;\, - 1;\,\,0;\,\,1;\,\,2} \right\}\)
- B \(x \in \left\{ { - 8;\,\, - 5;\,\, - 4;\,\, - 2;\, - 1;\,\,0;\,\,1;\,\,2} \right\}\)
- C \(x \in \left\{ { - 8;\,\, - 5;\,\, - 4;\,\, - 3;\, - 1;\,\,0;\,\,1;\,\,2} \right\}\)
- D \(x \in \left\{ { - 8;\,\, - 6;\,\, - 4;\,\, - 2;\, - 1;\,\,0;\,\,1;\,\,2} \right\}\)
Đáp án: C
Phương pháp giải:
Thêm bớt hạng tử, sau đó áp dụng quan hệ chia hết trong tập số nguyên.
Lời giải chi tiết:
Vì \({x^2} + 2\) là bội của \(x + 2\) nên \({x^2} + 2\,\, \vdots \,\,x + 2\).
\(\left. \begin{array}{l}{x^2} + 2\,\, \vdots \,\,x + 2\\x + 2\,\, \vdots \,\,x + 2\end{array} \right\} \Rightarrow \left. \begin{array}{l}{x^2} + 2x - 2x + 2\,\, \vdots \,\,x + 2\\x + 2\,\, \vdots \,\,x + 2\end{array} \right\}\)
\( \Rightarrow \left. \begin{array}{l}x\left( {x + 2} \right) - 2x + 2\,\, \vdots \,\,x + 2\\x + 2\,\, \vdots \,\,x + 2\end{array} \right\} \Rightarrow \left. \begin{array}{l} - 2x + 2\,\, \vdots \,\,x + 2\\x + 2\,\, \vdots \,\,x + 2\end{array} \right\} \Rightarrow \left\{ \begin{array}{l} - 2x + 2\,\, \vdots \,\,x + 2\\ - 2x - 4\,\, \vdots \,\,x + 2\end{array} \right. \Rightarrow 6\,\, \vdots \,\,x + 2\)
\( \Rightarrow x + 2 \in U\left( 6 \right) = \,\left\{ { \pm 1;\,\, \pm 2;\,\, \pm 3;\,\, \pm 6} \right\}\)
\( \Rightarrow x + 2 \in \left\{ { - 6;\,\, - 3;\,\, - 2;\,\, - 1;\,\,1;\,\,2;\,\,3;\,\,4} \right\}\)
\( \Rightarrow x \in \left\{ { - 8;\,\, - 5;\,\, - 4;\,\, - 3;\, - 1;\,\,0;\,\,1;\,\,2} \right\}\)
Chọn C.
Câu 2:
\(x - 1\) là ước của \({x^2} - 2x + 3.\)
- A \( x \in \left\{ { - 1;\,\, - 2;\,\,1;\,\,2} \right\}\)
- B \( x \in \left\{ { - 1;\,\, - 2;\,\,2;\,\,3} \right\}\)
- C \( x \in \left\{ { - 3;\,\, - 2;\,\,2;\,\,3} \right\}\)
- D \( x \in \left\{ { - 3;\,\, - 1;\,\,2;\,\,3} \right\}\)
Đáp án: B
Phương pháp giải:
Thêm bớt hạng tử, sau đó áp dụng quan hệ chia hết trong tập số nguyên.
Lời giải chi tiết:
Vì \(x - 1\) là ước của \({x^2} - 2x + 3\) nên \({x^2} - 2x + 3\,\, \vdots \,\,\left( {x - 1} \right) \Rightarrow {x^2} - x - x + 3\,\, \vdots \,\,\left( {x - 1} \right)\)
\( \Rightarrow x\left( {x - 1} \right) - x + 3\,\, \vdots \,\,\left( {x - 1} \right)\)
\( \Rightarrow - x + 3\,\, \vdots \,\,x - 1\)
Ta có: \(\left. \begin{array}{l} - x + 3\,\, \vdots \,\,x - 1\\x - 1\,\, \vdots \,\,x - 1\end{array} \right\} \Rightarrow 2\,\, \vdots \,\,x - 1 \Rightarrow x - 1 \in U\left( 2 \right) = \left\{ { - 2;\,\, - 1;\,\,1;\,\,2} \right\}\)
\( \Rightarrow x \in \left\{ { - 1;\,\, - 2;\,\,2;\,\,3} \right\}\).
Chọn B.
Câu hỏi 15 :
Tìm \(x,y \in \mathbb{Z}\), biết:
Câu 1:
\(\left( {2x - 1} \right)\left( {y - 4} \right) = - 13\)
- A \(\left( {x;\,y} \right) \in \left\{ {\left( { - 9;\,\,5} \right);\left( { - 1;\,\,17} \right);\left( {0;\,\, - 6} \right);\left( {7;\,\,3} \right)} \right\}.\)
- B \(\left( {x;\,y} \right) \in \left\{ {\left( { - 6;\,\,5} \right);\left( { - 1;\,\,17} \right);\left( {0;\,\, - 9} \right);\left( {7;\,\,3} \right)} \right\}.\)
- C \(\left( {x;\,y} \right) \in \left\{ {\left( { - 9;\,\,5} \right);\left( { - 1;\,\,15} \right);\left( {0;\,\, - 6} \right);\left( {5;\,\,3} \right)} \right\}.\)
- D \(\left( {x;\,y} \right) \in \left\{ {\left( { - 6;\,\,5} \right);\left( { - 1;\,\,15} \right);\left( {0;\,\, - 9} \right);\left( {5;\,\,3} \right)} \right\}.\)
Đáp án: B
Phương pháp giải:
+) Xác định ước.
+) Lập bảng.
Lời giải chi tiết:
\(x,\,\,y \in \mathbb{Z}\) và \(\left( {2x - 1} \right)\left( {y - 4} \right) = - 13\) suy ra \(\left( {2x - 1} \right)\)và \(\left( {y - 4} \right)\) là ước của \( - 13.\)
Ta có bảng sau:
Vậy \(\left( {x;\,y} \right) \in \left\{ {\left( { - 6;\,\,5} \right);\left( { - 1;\,\,17} \right);\left( {0;\,\, - 9} \right);\left( {7;\,\,3} \right)} \right\}.\)
Chọn B.
Câu 2:
\(\left( {5x + 1} \right)\left( {y - 1} \right) = 4.\)
- A \(\left( {x;\,y} \right) \in \left\{ {\left( { - 1;\,0} \right);\left( {1; - \,4} \right)} \right\}\)
- B \(\left( {x;\,y} \right) \in \left\{ {\left( { - 1;\,0} \right);\left( {1;\,4} \right)} \right\}\)
- C \(\left( {x;\,y} \right) \in \left\{ {\left( {1;\,0} \right);\left( { - 1;\,4} \right)} \right\}\)
- D \(\left( {x;\,y} \right) \in \left\{ {\left( {1;\,0} \right);\left( {1; - \,4} \right)} \right\}\)
Đáp án: C
Phương pháp giải:
+) Xác định ước.
+) Lập bảng.
Lời giải chi tiết:
\(x,\,\,y \in \mathbb{Z}\) và \(\left( {5x + 1} \right)\left( {y - 1} \right) = 4\) nên ta có bảng sau:
Vậy \(\left( {x;\,y} \right) \in \left\{ {\left( { - 1;\,0} \right);\left( {1;\,4} \right)} \right\}\).
Chọn C.
Câu hỏi 16 :
Tìm các giá trị nguyên của \(x\) để phân số \(\frac{{2x + 1}}{{3x - 1}}\) có giá trị nguyên.
- A \(x = 0\)
- B \(x = 1\)
- C \(x = - 1\)
- D \(x = 2\)
Đáp án: A
Phương pháp giải:
Điều kiện để phân số \(\frac{A}{B}\) là số nguyên là \(A\,\, \vdots \,\,B\).
Lời giải chi tiết:
Để phân số \(\frac{{2x + 1}}{{3x - 1}}\) có giá trị nguyên thì \(\left( {3x - 1} \right)\) là ước của \(\left( {2x + 1} \right)\) tức là \(\left( {2x + 1} \right)\,\, \vdots \,\,\left( {3x - 1} \right)\).
Ta có: \(\left. \begin{array}{l}2x + 1\,\, \vdots \,\,3x - 1\\3x - 1\,\, \vdots \,\,3x - 1\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}3.\left( {2x + 1} \right)\,\, \vdots \,\,3x - 1\\2.\left( {3x - 1} \right)\,\, \vdots \,\,3x - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}6x + 3\,\, \vdots \,\,3x - 1\\6x - 2\,\, \vdots \,\,3x - 1\end{array} \right.\)
\( \Rightarrow \left( {6x + 3} \right) - \left( {6x - 2} \right)\,\, \vdots \,\,3x - 1\)
\( \Rightarrow 6x + 3 - 6x + 2\,\, \vdots \,\,3x - 1\)
\( \Rightarrow 5\,\, \vdots \,\,3x - 1\)
\( \Rightarrow 3x - 1 \in U\left( 5 \right) = \left\{ { - 5;\,\, - 1;\,\,1;\,\,5} \right\}\)
\( \Rightarrow 3x \in \left\{ { - 4;\,\,0;\,\,2;\,\,4} \right\}\)\( \Rightarrow x \in \left\{ {\frac{{ - 4}}{3};\,\,0;\,\,\frac{2}{3};\,\,4} \right\}\)
Mà \(x \in \mathbb{Z}\) nên \(x = 0\) (thỏa mãn)
Vậy \(x = 0\).
Chọn A.
Câu hỏi 17 :
Cho \(A = 1 + 2 - 3 - 4 + 5 + 6 \ldots - 99 - 100\).
a) \(A\) có chia hết cho \(2\), cho \(3\), cho \(5\) hay không?
b) \(A\) có bao nhiêu ước là số nguyên, số tự nhiên?
Phương pháp giải:
- Rút gọn biểu thức
- Tìm số ước:
+ Phân tích ra thừa só nguyên tố \(A = {a^x}.{b^y}.{c^z}...\)
+ Số ước là\(\left( {x + 1} \right)\left( {y + 1} \right)\left( {z + 1} \right)...\)
Lời giải chi tiết:
a) Ta có:
\(A = 1 + 2 - 3 - 4 + 5 + 6 \ldots - 99 - 100\)
\(\,\,\,\,\, = \left( {1 + 2 - 3 - 4} \right) + \left( {4 + 6 - 7 - 8} \right) + \ldots + \left( {97 + 98 - 99 - 100} \right)\)
\(\,\,\,\,\, = \left( { - 4} \right) + \left( { - 4} \right) + \ldots + \left( { - 4} \right)\)
\(\,\,\,\,\, = 25.\left( { - 4} \right)\)
\(\,\,\,\,\, = - 100\)
Suy ra, \(A\) chia hết cho \(2\) và \(5\) nhưng không chia hết cho \(3\).
b) Xét \(100 = {2^2}{.5^2} \Rightarrow \)\(100\) có tất cả \(\left( {2 + 1} \right)\left( {2 + 1} \right) = 9\) ước.
\( \Rightarrow \)\(A\) có \(9\) ước tự nhiên và \(18\) ước nguyên.
Câu hỏi 18 :
Tìm các số nguyên \(n\) sao cho:
Câu 1:
\(2n - 1\) là ước của \(15\)
- A \(n \in \left\{ { - 3;\,\, - 2;\,\, - 1;\,\,0;\,\,1;\,\,2;\,\,3} \right\}\)
- B \(n \in \left\{ { - 7;\,\, - 3;\,\, - 2;\,\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,7} \right\}\)
- C \(n \in \left\{ { - 8;\,\, - 3;\,\, - 2;\,\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,8} \right\}\)
- D \(n \in \left\{ { - 7;\,\, - 2;\,\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,8} \right\}\)
Đáp án: D
Phương pháp giải:
+) Phân tích giá tri tuyệt đối của số đó ra thừa số nguyên tố rồi tìm các ước của chúng (Ước là các số tự nhiên và số đối của chúng)
+) Áp dụng:
\(\left. \begin{array}{l}a\,\, \vdots \,\,c\\b\,\, \vdots \,\,c\end{array} \right\} \Leftrightarrow a \pm b\,\, \vdots \,\,c\)
\(a\,\, \vdots \,\,c \Rightarrow ka\,\, \vdots \,\,c\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết:
Vì \(2n - 1\) là ước của \(15\) nên \(2n - 1 \in U\left( {15} \right) = \left\{ { \pm 15;\,\, \pm 5;\,\, \pm 3;\,\, \pm 1} \right\}\)

Vậy \(n \in \left\{ { - 7;\,\, - 2;\,\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,8} \right\}\).
Chọn D.
Câu 2:
\(3n + 4\) chia hết cho \(n - 3\)
- A \(n \in \left\{ { - 10; - 1;2;16} \right\}\)
- B \(n \in \left\{ { - 10; - 2;4;16} \right\}\)
- C \(n \in \left\{ { - 8; - 1;2;12} \right\}\)
- D \(n \in \left\{ { - 8; - 2;4;12} \right\}\)
Đáp án: B
Phương pháp giải:
+) Phân tích giá tri tuyệt đối của số đó ra thừa số nguyên tố rồi tìm các ước của chúng (Ước là các số tự nhiên và số đối của chúng)
+) Áp dụng:
\(\left. \begin{array}{l}a\,\, \vdots \,\,c\\b\,\, \vdots \,\,c\end{array} \right\} \Leftrightarrow a \pm b\,\, \vdots \,\,c\)
\(a\,\, \vdots \,\,c \Rightarrow ka\,\, \vdots \,\,c\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}3n + 4\,\, \vdots \,\,n - 3\\n - 3\,\, \vdots \,\,n - 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}3n + 4\,\, \vdots \,\,n - 3\\3n - 9\,\, \vdots \,\,n - 3\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \left( {3n + 4} \right) - \left( {3n - 9} \right)\,\, \vdots \,\,n - 3 \Rightarrow 13\,\, \vdots \,\,n - 3.\\ \Rightarrow n - 3 \in U\left( {13} \right) = \left\{ { - 13; - 1;\,\,1;\,\,13} \right\}.\end{array}\)
\( \Rightarrow \left[ \begin{array}{l}n - 3 = - 13\\n - 3 = - 1\\n - 3 = 1\\n - 3 = 13\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 13 + 3\\n = - 1 + 3\\n = 1 + 3\\n = 13 + 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}n = - 10\\n = 2\\n = 4\\n = 16\end{array} \right..\)
Vậy \(n \in \left\{ { - 10; - 2;\,\,4;\,\,16} \right\}.\)
Chọn B.
Câu 3:
\(n + 1\) là ước của \({n^2} + 7\)
- A \(n \in \left\{ { - 7; - 5; - 3; - 2;0;2;3;7} \right\}\)
- B \(n \in \left\{ { - 9; - 5; - 3; - 2;0;1;3;7} \right\}\)
- C \(n \in \left\{ { - 9; - 5; - 3; - 2;0;1;2;9} \right\}\)
- D \(n \in \left\{ { - 9; - 7; - 3; - 2;0;1;2;3;7} \right\}\)
Đáp án: B
Phương pháp giải:
+) Phân tích giá tri tuyệt đối của số đó ra thừa số nguyên tố rồi tìm các ước của chúng (Ước là các số tự nhiên và số đối của chúng)
+) Áp dụng:
\(\left. \begin{array}{l}a\,\, \vdots \,\,c\\b\,\, \vdots \,\,c\end{array} \right\} \Leftrightarrow a \pm b\,\, \vdots \,\,c\)
\(a\,\, \vdots \,\,c \Rightarrow ka\,\, \vdots \,\,c\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết:
a) Ta có: \({n^2} + 7\,\, \vdots \,\,n + 1 \Rightarrow {n^2} + n - n - 1 + 8\,\, \vdots \,\,n + 1\)
\(\begin{array}{l} \Rightarrow n\left( {n + 1} \right) - \left( {n + 1} \right) + 8\,\, \vdots \,\,n + 1\\ \Rightarrow \left( {n - 1} \right)\left( {n + 1} \right) + 8\,\, \vdots \,\,n + 1\end{array}\)
Vì \(n + 1\,\,\, \vdots \,\,n + 1\,\,\forall n \Rightarrow \left( {n + 1} \right)\left( {n - 1} \right)\,\, \vdots \,\,\,n + 1\)
\(\begin{array}{l} \Rightarrow 8\,\, \vdots \,\,\,n + 1\\ \Rightarrow n + 1 \in U\left( 8 \right) = \left\{ { - 8; - 4; - 2; - 1;\,\,1;\,\,2;\,\,4;\,\,8} \right\}\end{array}\)
Ta có bảng giá trị:

Vậy \(n \in \left\{ { - 9; - 5; - 3; - 2;\,\,0;\,\,1;\,\,3;\,\,7} \right\}.\)
Chọn B.
Câu hỏi 19 :
Cho \(x;\,y\in \mathbb{Z}\). Chứng minh rằng:
Nếu \(5x+47y\) chia hết cho 17 thì \(x+6y\) cũng chia hết cho 17.
Phương pháp giải:
+ Biến đổi để tách \(5x+47y\) thành tổng của hai số, trong đó một số chia hết cho 17 và một số chứa nhân tử \(x+6y\).
+ Sử dụng tính chất chia hết trên tập hơp các số nguyên để chứng minh.
Lời giải chi tiết:
Ta có:
\(\begin{align} & 5x+47y=5x+30y+17y \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\left( 5x+30y \right)+17y \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=5\left( x+6y \right)+17y \\ \end{align}\)
Vì \(5x+47y\) chia hết cho 17 và 17y chia hết cho 17 nên suy ra \(5\left( x+6y \right)\) chia hết cho 17.
Mà 5 không chia hết cho 17 nên suy ra \(x+6y\) chia hết cho 17.
Vậy nếu \(5x+47y\) chia hết cho 17 thì \(x+6y\) cũng chia hết cho 17.
Câu hỏi 20 :
Cho \(x,\,\,y \in \mathbb{Z}\). Chứng minh rằng: \(6x + 11y\) là bội của \(31\) khi và chỉ khi \(x + 7y\) là bội của \(31\).
Phương pháp giải:
Áp dụng các công thức:
+) \(a \pm b \vdots d \Leftrightarrow \left\{ \begin{array}{l}a + b \vdots d\\a - b \vdots d\end{array} \right.\)
+) \({\rm{a}}\, \vdots \,{\rm{b}} \Rightarrow {\rm{k}}{\rm{.a}}\, \vdots \,{\rm{b}}\)
Lời giải chi tiết:
Ta có: \(\left( {6x + 11y} \right) - 6\left( {x + 7y} \right) = 6x + 11y - 6x - 42y = \left( {6x - 6x} \right) + \left( {11y - 42y} \right) = - 31y\)
Vì \( - 31\,\, \vdots \,\,31 \Rightarrow - 31y\,\, \vdots \,\,31 \Rightarrow \left( {6x + 11y} \right) - 6\left( {x + 7y} \right)\,\, \vdots \,\,31\)
Suy ra, \(\left( {6x + 11y} \right)\) chia hết cho \(31\) khi và chỉ khi \(\left( {x + 7y} \right)\) chia hết cho \(31\).
Vậy \(6x + 11y\) là bội của \(31\) khi và chỉ khi \(x + 7y\) là bội của \(31\).
>> Học trực tuyến lớp 6 chương trình mới trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 6 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |