25 bài tập hai mặt phẳng song song mức độ vận dụng, vận dụng cao
Làm đề thiCâu hỏi 1 :
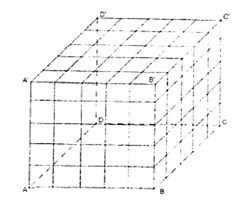
Cho khối lập phương \(ABCD.{{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}}.\) Người ta dùng 12 mặt phẳng phân biệt (trong đó, 4 mặt song song với (ABCD), 4 mặt song song với \(\left( A{{A}^{'}}{{B}^{'}}B \right)\) và 4 mặt song song với \(\left(A{{A}^{'}}{{D}^{'}}D \right)\), chia khối lập phương nhỏ rời nhau và bằng nhau. Biết rằng tổng diện tích tất cả các khối lập phương nhỏ bằng 480. Tính độ dài a của khối lập phương \(ABCD.{{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}}.\)
- A \(a=2\).
- B \(a=2\sqrt{3}.\)
- C \(a=2\sqrt{5}.\)
- D \(a=4.\)
Đáp án: D
Lời giải chi tiết:
Phương pháp:
Diện tích toàn phần của hình lập phương cạnh a là \({{S}_{tp}}=6{{a}^{2}}\).
Cách giải
Khi dùng các mặt phẳng như đề bài cho để chia khối lập phương ABCD.A’B’C’D’ ta được 125 khối lập phương nhỏ bằng nhau.
Do đó diện tích toàn phần của 1 khối lập phương nhỏ là \(\frac{480}{125}=\frac{96}{25}\)
Gọi cạnh hình lập phương ABCD.A’B’C’D’ bằng a thì độ dài cạnh hình lập phương nhỏ bằng \(\frac{a}{5}\).
Suy ra diện tích toàn phần của 1 hình lập phương nhỏ là:\(6{{\left( \frac{a}{5} \right)}^{2}}=\frac{96}{25}\Leftrightarrow a=4\)
Chọn D.
Câu hỏi 2 :
Cho tứ diện ABCD có có tất cả các cạnh đều bằng a. Gọi M là trung điểm của AB. Mp(P) qua M và song song với BC và CD cắt tứ diện theo 1 thiết diện là:
- A Một tam giác cân
- B Một tam giác đều
- C Một hình bình hành
- D Một tứ giác
Đáp án: B
Phương pháp giải:
- Dựng thiết diện dựa vào các yếu tố song song.
- Dựa vào tính chất đường trung bình của tam giác để tính các cạnh của thiết diện.
Lời giải chi tiết:
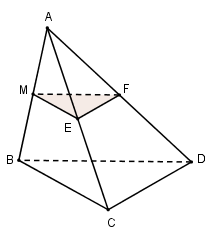
Gọi E và E lần lượt là trung điểm của AC và AD ta có ME // BC, EF // CD
\(\begin{array}{l}\left\{ \begin{array}{l}M \in \left( P \right) \cap \left( {ABC} \right)\\\left( P \right)\parallel BC \subset \left( {ABC} \right)\\ME\parallel {\rm{BC}}\end{array} \right. \Rightarrow \left( P \right) \cap \left( {ABC} \right) = ME\pi \\\left\{ \begin{array}{l}E \in \left( P \right) \cap \left( {ACD} \right)\\\left( P \right)\parallel CD \subset \left( {ACD} \right)\\{\rm{EF}}\parallel CD\end{array} \right. \Rightarrow \left( P \right) \cap \left( {ACD} \right) = EF\\\left( P \right) \cap \left( {ABD} \right) = MF\end{array}\)
Khi đó thiết diện tạo bởi mp(P) và hình chóp là tam giác MEF.
Ta có: \(ME = \frac{1}{2}BC = \frac{1}{2}a,EF = \frac{1}{2}CD = \frac{1}{2}a,MF = \frac{1}{2}BD = \frac{1}{2}a \Rightarrow ME = EF = MF = \frac{a}{2}\)
Vậy thiết diện là một tam giác đều.
Chọn B.
Câu hỏi 3 :
Cho tứ diện ABCD có BCD là tam giác đều cạnh a. Gọi I là trung điểm của AB. Mp(P) qua I song song với (BCD). Thiết diện của tứ diện cắt bởi mp(P) có diện tích là:
- A \(\frac{{{a}^{2}}\sqrt{3}}{4}\)
- B \(\frac{{{a}^{2}}\sqrt{3}}{8}\)
- C \(\frac{{{a}^{2}}\sqrt{3}}{12}\)
- D \(\frac{{{a}^{2}}\sqrt{3}}{16}\)
Đáp án: D
Phương pháp giải:
- Dựng thiết diện khi biết các yếu tố song song.
- Chứng minh thiết diện vừa dựng được là tam giác đều
- Tính diện tích tam giác đều bằng công thức tính nhanh: Diện tích tam giác đều cạnh a là \(S=\frac{{{a}^{2}}\sqrt{3}}{4}\).
Lời giải chi tiết:
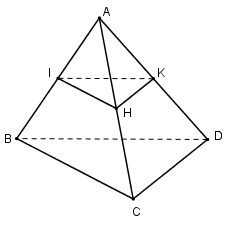
Gọi H và K lần lượt là trung điểm của AC và AD ta có:
\(\left\{ \begin{array}{l}I \in \left( {ABC} \right) \cap \left( \alpha \right)\\\left( \alpha \right)\parallel BC \subset \left( {ABC} \right)\\IH\parallel BC\end{array} \right. \Rightarrow \left( {ABC} \right) \cap \left( \alpha \right) = IH\)
Tương tự ta chứng minh được \(\left( \alpha \right)\cap \left( ACD \right)=HK\,\,;\,\,\left( \alpha \right)\cap \left( ABD \right)=IK\)
Vậy thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) qua I và song song với (BCD) là tam giác IHK.
Ta có: IH, HK, IK lần lượt là đường trung bình của các tam giác ABC, ACD, ABD.
\(IH=\frac{1}{2}BC=\frac{1}{2}a,HK=\frac{1}{2}CD=\frac{1}{2}a,IK=\frac{1}{2}BD=\frac{1}{2}a\Rightarrow IH=HK=IK=\frac{a}{2}\Rightarrow \Delta IHK\(đều cạnh \(\frac{a}{2}.\)
Vậy \({{S}_{\Delta IHK}}={{\left( \frac{a}{2} \right)}^{2}}\frac{\sqrt{3}}{4}=\frac{{{a}^{2}}\sqrt{3}}{16}.\)
Chọn D.
Câu hỏi 4 :
Cho đường thẳng a và mp(P). Trong các mệnh đề sau mệnh đề nào đúng ?
- A \(b\subset \left( P \right),b\parallel a\Rightarrow a\parallel \left( P \right)\)
- B Giả sử a // (P), khi đó nếu b // (P) thì a // b.
- C a // (P)\(\Rightarrow \) a // b, \(\forall b\subset \left( P \right).\)
- D Nếu a // (P) thì tồn tại duy nhất một (Q) qua a // (P).
Đáp án: D
Phương pháp giải:
Suy ra trực tiếp từ các đáp án. Sử dụng quan hệ song song của đường thẳng và mặt phẳng.
Lời giải chi tiết:
A sai vì a có thể nằm trong (P).
B sai vì a và b có thể cắt nhau và cùng nằm trong một mặt phẳng song song với (P)
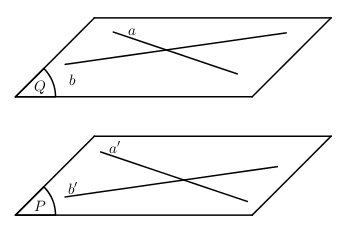
Ta thấy
\(\begin{array}{l}a\parallel a' \subset \left( P \right) \Rightarrow a\parallel \left( P \right)\,\,\,\left( {a \not\subset \left( P \right)} \right)\\b\parallel b' \subset \left( P \right) \Rightarrow b\parallel \left( P \right)\,\,\,\left( {b \not\subset \left( P \right)} \right)\end{array}\)
Tuy nhiên a và b không song song với nhau.
C sai. Dựa vào hình vẽ trên ta thấy a // (P) thì \(a\parallel a'\subset \left( P \right)\,\,;\,\,ab'\subset \left( P \right)\).
Chọn D.
Câu hỏi 5 :
Trong không gian cho đường thẳng \(a\subset \left( \alpha \right),b\subset \left( \beta \right),\left( \alpha \right)\parallel \left( \beta \right).\) Kết quả nào sau đây đúng?
- A \(a\parallel b\)
- B a chéo b
- C a cắt b
- D a,b không có điểm chung.
Đáp án: D
Phương pháp giải:
Suy ra trực tiếp từ các đáp án, vẽ hình minh họa để nhìn rõ hơn.
Lời giải chi tiết:
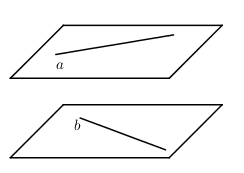
Khi 2 đường thẳng a và b lần lượt thuộc 2 mặt phẳng song song ta chưa thể kết luận chúng song song hay chéo nhau nhưng chắc chắn chúng không có điểm chung.
Chọn D.
Câu hỏi 6 :
Cho tứ diện đều ABCD có các cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó diện tích của thiết diện của hình tứ diện khi cắt bởi mp\(\left( \alpha \right)\)đi qua M và song song với (ACD) là:
- A \(\frac{{{\left( a+m \right)}^{2}}\sqrt{3}}{4}\)
- B \(\frac{{{\left( a-m \right)}^{2}}\sqrt{3}}{4}\)
- C \(\frac{{{\left( a-m \right)}^{2}}\sqrt{2}}{2}\)
- D \(\frac{{{m}^{2}}\sqrt{3}}{4}\)
Đáp án: B
Phương pháp giải:
- Tìm thiết diện dựa vào các yếu tố song song.
- Sử dụng định lí Ta-let đảo.
- Chứng minh thiết diện là tam giác đều và sử dụng công thức tính diện tích tam giác đều cạnh a là: \(S=\frac{{{a}^{2}}\sqrt{3}}{4}.\)
Lời giải chi tiết:
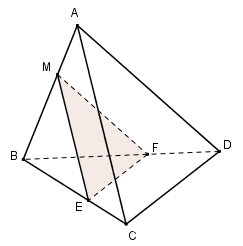
Trong (ABC) qua M kẻ đường thẳng song song với AC cắt BC tại E \(\Rightarrow \left( \alpha \right)\cap \left( ABC \right)=ME\).
Trong (ABD) qua M kẻ đường thẳng song song với AD cắt BD tại F \(\Rightarrow \left( \alpha \right)\cap \left( ABD \right)=MF.\)
\(\Rightarrow \left( \alpha \right)\cap \left( BCD \right)=EF.\)
Vậy thiết diện cần tìm là tam giác MEF.
Ta có: \(ME\parallel CD\Rightarrow \frac{ME}{CD}=\frac{BM}{AB}\Leftrightarrow \frac{ME}{a}=\frac{a-m}{a}\Leftrightarrow ME=a-m.\)
\(\text{EF}\parallel CD\Rightarrow\frac{EF}{CD}=\frac{BE}{BC}=\frac{ME}{AC}\Leftrightarrow \frac{EF}{a}=\frac{a-m}{a}\Rightarrow EF=a-m\).
Chứng minh tương tự ta có MF = a – m.. Suy ra tam giác MEF đều cạnh a – m.
Vậy \({{S}_{MEF}}=\frac{{{\left( a-m \right)}^{2}}\sqrt{3}}{4}.\)
Chọn B.
Câu hỏi 7 :
Cho hình chóp S.ABCD có đáy là hình bình hành. Mặt phẳng \(\left( \alpha \right)\) cắt SA, SB, SC, SD theo thứ tự lần lượt tại A’, B’, C’, D’ (không đồng thời trùng với các đầu mút). \(A'B'C'D'\) là hình bình hành khi và chỉ khi:
- A \(\left( \alpha \right)//\left( {ABCD} \right)\)
- B \(\left( \alpha \right)\) và (ABCD) cắt nhau.
- C \(\left( \alpha \right)\) và (ABCD) trùng nhau.
- D \(\left( \alpha \right)\) đi qua trung điểm của các đoạn SA, SB, SC, SD.
Đáp án: A
Phương pháp giải:
Suy luận từng đáp án.
Lời giải chi tiết:
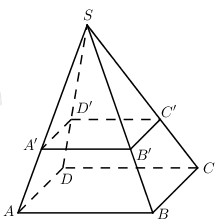
Do A’, B’, C’, D’ không đồng thời trùng với các đầu mút nên loại đáp án C.
Gọi a là đường thẳng qua S và song song với AB, b là đường thẳng qua S và song song với AD.
A’B’C’D’ là hình bình hành khi và chỉ khi \(\left\{ \begin{array}{l}A'B'//C'D'\\A'B' = C'D'\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}a = \left( {ABC} \right) \cap \left( {SCD} \right)\\A'B'//C'D'\\A'B' \subset \left( {ABC} \right),\,\,C'D' \subset \left( {SCD} \right)\end{array} \right. \Rightarrow A'B'//a\)
Suy ra A’B’ // AB (1)
Tương tự ta có: \(\left\{ \begin{array}{l}b = \left( {ABD} \right) \cap \left( {SBC} \right)\\A'D'//B'C'\\A'D' \subset \left( {ABD} \right),\,\,C'B' \subset \left( {SBC} \right)\end{array} \right. \Rightarrow A'D'//b\)
Suy ra A’D’ // AD (2).
Từ (1) và (2) \( \Rightarrow \left( {A'B'C'D'} \right)//\left( {ABCD} \right)\) hay \(\left( \alpha \right)//\left( {ABCD} \right)\).
Chọn A.
Câu hỏi 8 :
Cho hai hình vuông có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Trên các đường chéo AC và BF ta lấy các điểm M, N sao cho AM = BN. Mặt phẳng (P) chứa MN và song song với AB cắt AD và AF lần lượt tại M’, N’. Khẳng định nào sau đây là đúng?
- A AC, BF cắt nhau
- B Tứ giác MNM’N’ là hình bình hành
- C MN song song với (DEF)
- D MN cắt (DEF)
Đáp án: C
Phương pháp giải:
+) Trong (ABCD) qua M kẻ MM’ // AB \(\left( {M' \in AD} \right)\)
Trong (ABEF) qua N kẻ NN’ // AB \(\left( {N' \in AF} \right)\)
+) Dựa vào phương pháp chứng minh hai mặt phẳng song song: Hai đường thẳng cắt nhau trong mặt phẳng này lần lượt song song với hai đường thẳng trong mặt phẳng kia thì hai mặt phẳng đó song song
và tính chất: Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này song song với mặt phẳng kia.
Lời giải chi tiết:
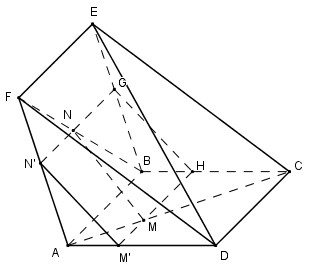
Trong (ABCD) qua M kẻ MM’ // AB \(\left( {M' \in AD} \right)\)
Trong (ABEF) qua N kẻ NN’ // AB \(\left( {N' \in AF} \right)\)
Ta có:
\(\left\{ \matrix{ {{AM'} \over {AD}} = {{AM} \over {AC}} \hfill \cr {{AN'} \over {AF}} = {{BN} \over {BF}} \hfill \cr AM = BN;AC = BF \hfill \cr} \right. \Rightarrow {{AM'} \over {AD}} = {{AN'} \over {AF}} \Rightarrow M'N'//DF\)
Lại có NN’ // AB // EF \( \Rightarrow \left( {MM'N'N} \right)//\left( {DEF} \right)\)
Mà \(MN \subset \left( {MM'N'N} \right) \Rightarrow MN//\left( {DEF} \right)\)
Chọn C.
Câu hỏi 9 :
Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 4, \(\widehat {BAC} = {30^0}\). Mặt phẳng (P) song song với (ABC) cắt đoạn SA tại M sao cho SM = 2MA. Biện tích thiết diện của (P) và hình chóp S.ABC bằng bao nhiêu?
- A \({{16} \over 9}\)
- B \({{14} \over 9}\)
- C \({{25} \over 9}\)
- D 1
Đáp án: A
Phương pháp giải:
Qua M kẻ các đường thẳng song song với AB và AC. Xác định mặt phẳng (P) và thiết diện của (P) với hình chóp là tam giác MNP.
Chứng minh thiết diện là tam giác đồng dạng với tam giác ABC theo tỉ số k nào đó \( \Rightarrow {{{S_{MNP}}} \over {{S_{ABC}}}} = {k^2}\).
Tính diện tích tam giác ABC từ đó suy ra diện tích tam giác MNP.
Lời giải chi tiết:
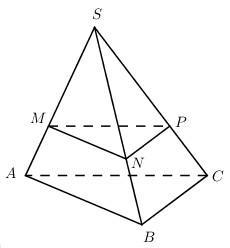
Trong (SAB) qua M kẻ MN // AB, trong (SAC) kẻ MP // AC. Khi đó ta có (MNP) // (ABC).
\( \Rightarrow \left( {MNP} \right) \equiv \left( P \right)\).
Thiết diện của (P) và hình chóp là tam giác MNP đồng dạng với tam giác ABC theo tỉ số \({{MN} \over {AB}} = {{SM} \over {SA}} = {2 \over 3}\)
\( \Rightarrow {{{S_{MNP}}} \over {{S_{ABC}}}} = {\left( {{2 \over 3}} \right)^2} = {4 \over 9} \Rightarrow {S_{MNP}} = {4 \over 9}{S_{ABC}}\)
Ta có \({S_{ABC}} = {1 \over 2}AB.AC.\sin \widehat {BAC} = {1 \over 2}.4.4.\sin {30^0} = 4\)
\( \Rightarrow {S_{MNP}} = {4 \over 9}.4 = {{16} \over 9}\)
Chọn A.
Câu hỏi 10 :
Cho hình chóp S.ABCD có đáy ABCD là hình thang có các đáy AD và BC. Gọi M là trọng tâm tam giác SAD, N là điểm thuộc AC sao cho \(NA = {{NC} \over 2}\), P là điểm thuộc đoạn CD sao cho \(PD = {{PC} \over 2}\). Khi đó mệnh đề nào sau đây là đúng?
- A MN // (SBC) và (MNP) // (SBC).
- B MN cắt (SBC)
- C Giao tuyến của hai mặt phẳng (SBC) và (MNP) là đường thẳng song song với BC.
- D (MNP) // (SAD)
Đáp án: A
Phương pháp giải:
Dựa vào phương pháp chứng minh hai mặt phẳng song song: Hai đường thẳng cắt nhau trong mặt phẳng này lần lượt song song với hai đường thẳng trong mặt phẳng kia thì hai mặt phẳng đó song song và tính chất: Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này song song với mặt phẳng kia.
Lời giải chi tiết:
Gọi \(H \in SD\) sao cho \(HD = {1 \over 2}SH\)
Ta có: \({{SM} \over {SE}} = {{SH} \over {SD}} = {2 \over 3} \Rightarrow MH//AD//NP \Rightarrow M,H,P,N\) đồng phẳng.
Ta có:
\(\eqalign{ & {{AN} \over {AC}} = {{DP} \over {DC}} = {1 \over 3} \Rightarrow NP//AD;\,\,{{DH} \over {DS}} = {{DP} \over {DC}} = {1 \over 3} \Rightarrow HP//SC \cr & \left\{ \matrix{ NP//AD//BC \hfill \cr HP//SC \hfill \cr} \right. \Rightarrow \left( {MHPN} \right)//\left( {SBC} \right) \Rightarrow \left( {MNP} \right)//\left( {SBC} \right) \cr & MN \subset \left( {MNP} \right) \Rightarrow MN//\left( {SBC} \right) \cr} \)
Chọn A.
Câu hỏi 11 :
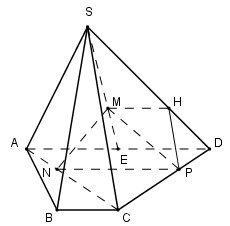
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, SD. Gọi P, Q, R lần lượt là trung điểm của AB, ON, SB. Chọn mệnh đề sai trong các mệnh đề sau:
- A PQ cắt (SBC)
- B (MOR) // (SCD)
- C (MON) // (SBC)
- D PQ // (SBC)
Đáp án: A
Phương pháp giải:
Dựa vào phương pháp chứng minh hai mặt phẳng song song: Hai đường thẳng cắt nhau trong mặt phẳng này lần lượt song song với hai đường thẳng trong mặt phẳng kia thì hai mặt phẳng đó song song và tính chất: Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này song song với mặt phẳng kia.
Lời giải chi tiết:
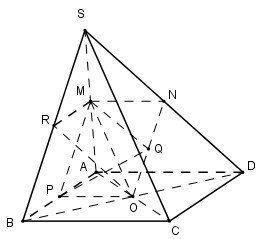
\(\left\{ \matrix{ MR//AB//CD \hfill \cr OR//SD \hfill \cr} \right. \Rightarrow \left( {MOR} \right)//\left( {SCD} \right) \Rightarrow B\) đúng.
\(\left\{ \matrix{ MN//AD//BC \hfill \cr ON//SB \hfill \cr} \right. \Rightarrow \left( {MON} \right)//\left( {SBC} \right) \Rightarrow C\) đúng.
Ta có:
\(\left\{ \matrix{ MP//SB \hfill \cr OP//BC \hfill \cr} \right. \Rightarrow \left( {MNOP} \right)//\left( {SBC} \right);\,\,PQ \subset \left( {MNOP} \right) \Rightarrow PQ//\left( {SBC} \right) \Rightarrow D\) đúng.
Vậy A sai.
Chọn A.
Câu hỏi 12 :
Cho tứ diện ABCD, gọi \({G_1};{G_2};{G_3}\) lần lượt là trọng tâm các tam giác ABC, ACD, ADB. Diện tích thiết diện tạo bởi mặt phẳng \(\left( {{G_1}{G_2}{G_3}} \right)\) bằng k lần diện tích tam giác BCD, khi đó k bằng
- A \({4 \over 9}\)
- B \({2 \over 3}\)
- C \({3 \over 4}\)
- D \({1 \over 2}\)
Đáp án: A
Phương pháp giải:
+) Chứng minh \(\left( {{G_1}{G_2}{G_2}} \right)//\left( {MNP} \right) \Rightarrow \) Cách dựng thiết diện.
+) Chứng minh thiết diện vừa dựng được là tam giác đồng dạng với tam giác BCD.
+) Sử dụng tính chất: Tỉ số diện tích bằng bình phương tỉ số đồng dạng.
Lời giải chi tiết:
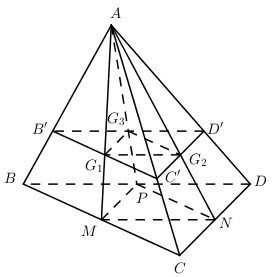
Gọi M, N, P lần lượt là trung điểm của BC, CD, BD. Ta có:
\(\eqalign{ & {{A{G_1}} \over {AM}} = {{A{G_2}} \over {AN}} = {{A{G_3}} \over {AP}} = {2 \over 3} \cr & \Rightarrow {G_1}{G_2}//MN,\,\,{G_2}{G_3}//NP \Rightarrow \left( {{G_1}{G_2}{G_2}} \right)//\left( {MNP} \right) \cr} \)
Qua \({G_1}\) kẻ \(B'C'//BC\,\,\left( {B' \in AB,C' \in AC} \right)\)
Qua \({G_2}\) kẻ \(C'D'//DC\,\,\left( {D' \in AD} \right)\)
Khi đó thiết diện của hình chóp cắt bởi \(\left( {{G_1}{G_2}{G_3}} \right)\) là \(\Delta B'C'D'\)
Ta có: \({{B'C'} \over {BC}} = {{A{G_1}} \over {AM}} = {2 \over 3} \Rightarrow \Delta B'C'D'\) đồng dạng với \(\Delta BCD\) theo tỉ số \({2 \over 3}\).
\( \Rightarrow {{{S_{\Delta B'C'D'}}} \over {{S_{\Delta BCD}}}} = {\left( {{2 \over 3}} \right)^2} = {4 \over 9}\).
Chọn A.
Câu hỏi 13 :
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành tâm \(O\) và có \(AC = a, BD = b\). Tam giác \(SBD\) là tam giác đều. Một mặt phẳng \((P)\) di động song song với \((SBD)\) đi qua \(I\) trên đoạn \(OC\). Đặt \(AI = x\,\,\left( {{a \over 2} < x < a} \right)\). Khi đó diện tích thiết diện của hình chóp với mặt phẳng \((P)\) là:
- A \({{{b^2}{{\left( {a - x} \right)}^2}\sqrt 2 } \over {{a^2}}}\)
- B \({{{b^2}{{\left( {a + x} \right)}^2}\sqrt 3 } \over {{a^2}}}\)
- C \({{{b^2}{{\left( {a + x} \right)}^2}} \over {{a^2}\sqrt 3 }}\)
- D \({{{b^2}{{\left( {a - x} \right)}^2}\sqrt 3 } \over {{a^2}}}\)
Đáp án: D
Phương pháp giải:
Dựng mặt phẳng qua I và song song với (SBD), dựng thiết diện.
Chứng minh thiết diện là tam giác đều và tính diện tích tam giác đều đó.
Lời giải chi tiết:
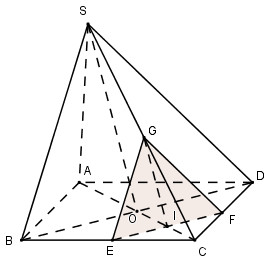
Trong (ABCD) qua I kẻ EF // BD \(\left( {E \in BC;F \in CD} \right)\)
Trong (SAC) qua I kẻ IG // SO \(\left( {G \in SC} \right)\)
\( \Rightarrow \left( {GEF} \right)\) qua I và song song với (SBD) \( \Rightarrow \left( P \right) \equiv \left( {GEF} \right)\)
Ta có: \(\left\{ \matrix{ \left( {GEF} \right) \cap \left( {SBC} \right) = GE \hfill \cr \left( {SBD} \right) \cap \left( {SBC} \right) = SB \hfill \cr \left( {GEF} \right)//\left( {SBD} \right) \hfill \cr} \right. \Rightarrow GE//SB\)
Tương tự ta chứng minh được GF // SD.
Ta có:
\(\left\{ \matrix{ {{IC} \over {OC}} = {{FE} \over {BD}} = {{GC} \over {SC}} = {{GE} \over {SB}} = {{GF} \over {SD}} \hfill \cr BD = SB = SD \hfill \cr} \right. \Rightarrow GE = GF = EF \Rightarrow \Delta GEF\) đều và \({{IC} \over {OC}} = {{EF} \over {BD}} \Rightarrow EF = {{IC} \over {OC}}.BD = {{2(a - x)} \over a}.b\)
\( \Rightarrow \Delta GEF\) đều cạnh \({{2(a - x)} \over a}.b\), do đó \({S_{\Delta GEF}} = {{{{4\left( {{{a - x} \over a}} \right)}^2}.{b^2}\sqrt 3 } \over 4} = {{{b^2}{{\left( {a - x} \right)}^2}\sqrt 3 } \over {{a^2}}}\)
Chọn D.
Câu hỏi 14 :
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB = 3a, AD = CD = a. Mặt bên (SAB) là tam giác cân tại S, SA = 2a. Mặt bên \(\left( \alpha \right)\) di động và song song với (SAB) đồng thời cắt các cạnh AD, BC, SC, SD theo thứ tự M, N, P, Q. Biết tứ giác MNPQ ngoại tiếp một đường tròn bán kính r. Tính r?
- A \(r = {{a\sqrt 7 } \over 6}\)
- B \(r = {{a\sqrt 7 } \over 3}\)
- C \(r = {{a\sqrt 7 } \over 2}\)
- D \(r = {{2a\sqrt 7 } \over 3}\)
Đáp án: A
Phương pháp giải:
Dựng mặt phẳng \(\left( \alpha \right)\) thỏa mãn yêu cầu bài toán, chứng minh thiết diện MNPQ là hình thang cân.
Chứng minh để MNPQ ngoại tiếp được đường tròn thì MN + PQ = MQ + NP (*).
Đặt AM = x. Tính các cạnh của hình thang MNPQ theo x rồi thay vào (*) để tìm x.
Tính bán kính mặt cầu nội tiếp hình thang cân MNPQ.
Lời giải chi tiết:
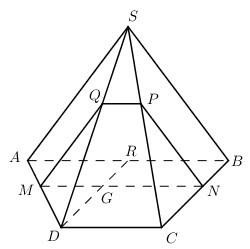
Lấy điểm \(M \in AD,\) trong (ABCD) qua M kẻ MN // AB \(\left( {N \in BC} \right)\). Trong (SAD) qua M kẻ MQ // SA, trong (SBC) qua N kẻ NP // SB.
\( \Rightarrow \left( {MNPQ} \right)//\left( {SAB} \right)\).
Ta có: \(\left\{ \matrix{ \left( {MNPQ} \right) \cap \left( {ABCD} \right) = MN \hfill \cr \left( {MNPQ} \right) \cap \left( {SCD} \right) = PQ \hfill \cr \left( {ABCD} \right) \cap \left( {SCD} \right) = CD \hfill \cr} \right. \Rightarrow MN//PQ//CD \Rightarrow \) MNPQ là hình thang.
Lại có \(\left\{ \matrix{ \widehat {QMN} = \widehat {\left( {MN;MQ} \right)} = \widehat {\left( {AB;AS} \right)} = \widehat {SAB} \hfill \cr \widehat {PNM} = \widehat {\left( {NM;NP} \right)} = \widehat {\left( {BA;BS} \right)} = \widehat {SBA} \hfill \cr} \right. \Rightarrow \widehat {QMN} = \widehat {PNM}\)
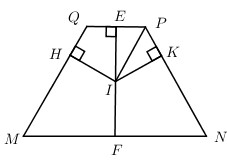
Do đó MNPQ là hình thang cân.
Giả sử MNPQ ngoại tiếp được đường tròn tâm I, gọi E và F lần lượt là trung điểm của PQ và MN.
Do MNPQ là hình thang cân nên \(I \in EF\).
Kẻ \(IH \bot MQ;\,\,IK \bot NP\).
Ta có: \(IE = IF = IH = IK\), xét tam giác vuông IPE và IPK có IC chung, IE = IK \( \Rightarrow \Delta IPE = \Delta IPK\,\,\left( {ch - cgv} \right) \Rightarrow EP = KP\)
Chứng minh tương tự ta có: \(QE = QH,\,\,NK = NF,\,\,MH = MF\)
\( \Rightarrow MN + PQ = MQ + NP = 2MQ\,\,\,\left( * \right)\)
Đặt AM = x (0 < x < a). Theo định lí Ta-let ta có: \({{DM} \over {DA}} = {{MQ} \over {SA}} \Rightarrow MQ = {{DM.SA} \over {DA}} = {{\left( {a - x} \right).2a} \over a} = 2\left( {a - x} \right)\)
Ta có : \({{PQ} \over {CD}} = {{SQ} \over {SD}} = {{AM} \over {AD}} \Rightarrow {{PQ} \over a} = {x \over a} \Rightarrow PQ = x\).
Kẻ DR // BC, gọi \(G = DR \cap MN\), dễ thấy RB = GN = CD = a.
\({{MG} \over {AR}} = {{DM} \over {DA}} \Rightarrow MG = {{AR.DM} \over {DA}} = {{2a.\left( {a - x} \right)} \over a} = 2\left( {a - x} \right) \Rightarrow MN = MG + GN = 3a - 2x\)
Thay vào (*) ta có : \(3a - 2x + x = 4\left( {a - x} \right) \Leftrightarrow 3a - x = 4a - 4x \Leftrightarrow 3x = a \Leftrightarrow x = {a \over 3}\).
\( \Rightarrow MN = {{7a} \over 3},\,\,MQ = {{4a} \over 3};\,\,PQ = {a \over 3}\)
Ta có : \(EF = \sqrt {M{Q^2} - {{\left( {{{MN - PQ} \over 2}} \right)}^2}} = {{a\sqrt 7 } \over 3} \Rightarrow r = {1 \over 2}EF = {{a\sqrt 7 } \over 6}.\)
Chọn A.
Câu hỏi 15 :
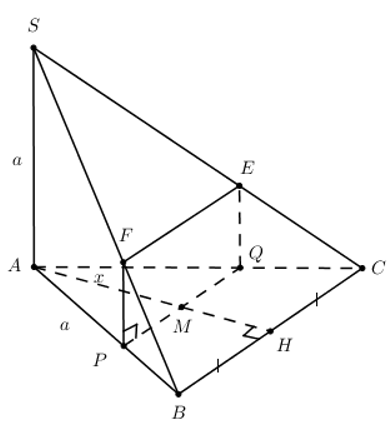
Chóp SABC. SA = a. \(SA\bot BC.\) Tam giác ABC đều. AB = a. H là trung điểm của BC. \(M\in AH\) để AM = x \(\left( 0<x<\frac{a\sqrt{3}}{2} \right).\) Mặt phẳng (P) đi qua M và song song với SA, BC. Dựng (P). Tìm thiết diện của mp (P) với hình chóp và tính diện tích thiết diện.
Lời giải chi tiết:
Dựng (P)
+) Qua M dựng \(PQ\parallel BC\)
+) Qua Q dựng \(QE\parallel SA\,\,\Rightarrow \left( P \right)\equiv \left( PQE \right)\)
Tìm thiết diện.
+) Ta có \(\left\{ \begin{align} & \left( PQE \right)\cap \left( ABC \right)=PQ \\ & \left( PQE \right)\cap \left( SAC \right)=QE \\\end{align} \right.\)
\(\begin{array}{l}
\left\{ \begin{array}{l}
E \in \left( {PQE} \right),\,E \in \left( {SBC} \right)\\
PQ\parallel BC
\end{array} \right.\\
\Rightarrow \left( {PQE} \right) \cap \left( {SBC} \right) = EF\parallel PQ\parallel BC\\
\Rightarrow \left( {PQE} \right) \cap \left( {SAB} \right) = PF
\end{array}\)
\(\Rightarrow\) Thiết diện là tứ giác PQEF.
\(+)\,\,\,SA\bot BC\Rightarrow PQ\bot QE\Rightarrow \) Thiết diện là hình chữ nhật.
Tính diện tích thiết diện
\(\begin{align} & +)\,\,PQ\parallel BC\Rightarrow \frac{PQ}{BC}=\frac{AM}{AH}\Rightarrow PQ=\frac{a.x}{\frac{a\sqrt{3}}{2}}=\frac{2x}{\sqrt{3}} \\ & +)\,\,QE\parallel SA\Rightarrow \frac{QE}{SA}=\frac{CQ}{CA}=\frac{HM}{HA}\Rightarrow QE=\frac{a.\left( \frac{a\sqrt{3}}{2}-x \right)}{\frac{a\sqrt{3}}{2}}=\frac{a\sqrt{3}-2x}{\sqrt{3}} \\ & +)\,{{S}_{TD}}={{S}_{EFPQ}}=PQ.QE=\frac{2x}{\sqrt{3}}.\frac{a\sqrt{3}-2x}{\sqrt{3}}=\frac{2}{3}x\left( a\sqrt{3}-2x \right) \\\end{align}\)
Câu hỏi 16 :
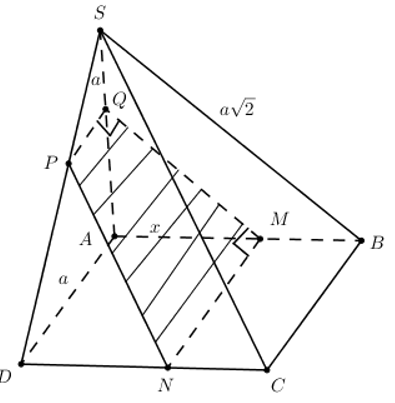
Chóp S.ABCD. SA = a. ABCD là hình vuông. AB = a. \(SB=a\sqrt{2},\,\widehat{SBC}={{90}^{o}}.\,M\in AB\,\) để AM = x (0< x < a). Mặt phẳng (P) qua M và song song với (SBC). Dựng mặt phẳng (P). Tìm thiết diện của mp (P) với hình chóp và tính diện tích thiết diện.
Lời giải chi tiết:
Dựng (P)
+) Qua M dựng \(MN\parallel BC\)
+) Qua M dựng \(MQ\parallel SB\)
\(\Rightarrow \left( P \right)\equiv \left( QMN \right)\)
Tìm thiết diện.
+) Ta có: \(\left\{ \begin{align} & \left( QMN \right)\cap \left( ABCD \right)=MN \\ & \left( QMN \right)\cap \left( SAB \right)=MQ \\\end{align} \right.\)
+) \(\left\{ \begin{align} & Q\in \left( QMN \right),\,Q\in \left( SAD \right) \\ & MN\parallel AD \\\end{align} \right.\)
\(\Rightarrow \left( QMN \right)\cap \left( SAD \right)=QP\parallel AD\parallel MN\)
\(\Rightarrow \left( QMN \right)\cap \left( SCD \right)=PN\Rightarrow \) Thiết diện là tứ giác MNPQ
Tính diện tích thiết diện
+) \(\widehat{SBC}={{90}^{o}}\Rightarrow \widehat{QMN}={{90}^{o}}\Rightarrow \) Thiết diện là hình thang vuông ở M, Q có MN = a.
\(\begin{align} & +)\,\,QM\parallel SB\Rightarrow \frac{QM}{SB}=\frac{AM}{AB}\Rightarrow QM=\frac{a\sqrt{2}.x}{a}=x\sqrt{2} \\ & +)\,\,PQ\parallel AD\Rightarrow \frac{PQ}{AD}=\frac{SQ}{SA}=\frac{BM}{BA}\Rightarrow PQ=\frac{\left( a-x \right)a}{a}=a-x \\ & +)\,{{S}_{TD}}=\frac{\left( MN+PQ \right).QM}{2}=\frac{\sqrt{2}x\left( 2a-x \right)}{2} \\\end{align}\)
Câu hỏi 17 :
Cho hai mặt phẳng song song \(\left( P \right),\left( Q \right)\) và đường thẳng \(\Delta \). Mệnh đề nào sau đây sai?
- A Nếu \(\Delta \) song song với \(\left( P \right)\) thì \(\Delta \) song song với \(\left( Q \right)\).
- B Nếu \(\Delta \) nằm trên \(\left( P \right)\) thì \(\Delta \) song song với \(\left( Q \right)\).
- C Nếu \(\Delta \) nằm trên \(\left( Q \right)\) thì \(\Delta \) song song với \(\left( P \right)\).
- D Nếu \(\Delta \) cắt \(\left( P \right)\) thì \(\Delta \) cắt \(\left( Q \right)\).
Đáp án: A
Phương pháp giải:
Nhận xét tính đúng sai của từng đáp án, sử dụng tính chất đường thẳng và mặt phẳng song song.
Chú ý chỉ ra phản ví dụ cho mệnh đề sai.
Lời giải chi tiết:
Đáp án A: sai vì nếu \(\Delta //\left( P \right)\) thì vẫn có thể xảy ra trường hợp \(\Delta \subset \left( Q \right)\) chứ chưa chắc đã song song.
Đáp án B, C: đúng theo tính chất hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này đều song song mặt phẳng kia.
Đáp án D: hiển nhiên đúng.
Chọn A.
Câu hỏi 18 :
Cho lăng trụ \(ABCD.A'B'C'D'\) có hai đáy là các hình bình hành. Các điểm \(M,N,P\) lần lượt là trung điểm của cạnh \(AD,BC,CC'\) (tham khảo hình vẽ). Xét các khẳng định sau:
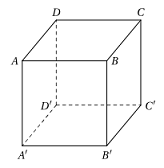
I) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(A'D'\)
II) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại trung điểm của \(DD'\)
III) Mặt phẳng \(\left( {MNP} \right)\) song song với mặt phẳng \(\left( {ABC'D'} \right)\)
Trong các khẳng định trên, số khẳng định đúng là
- A \(3\)
- B \(1\)
- C \(4\)
- D \(2\)
Đáp án: D
Phương pháp giải:
Sử dụng cách tìm giao điểm của đường thẳng và mặt phẳng
Chứng minh hai mặt phẳng \(\left( P \right),\left( Q \right)\) song song dựa vào \(\left\{ \begin{array}{l}a//b\\c//d\\a,c \subset \left( P \right),a \cap c\\b,d \subset \left( Q \right),b \cap d\end{array} \right. \Rightarrow \left( P \right)//\left( Q \right)\)
Lời giải chi tiết:
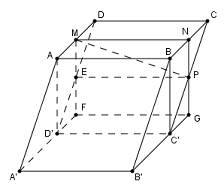
+ Lấy \(E\) là trung điểm \(DD' \Rightarrow EP//CD//MN\) suy ra \(\left( {MNP} \right) \equiv \left( {MNPE} \right)\)
Do đó \(\left( {MNP} \right) \cap DD' = E\) với \(E\) là trung điểm \(DD'\) nên II) đúng.
+ Trong \(\left( {ADD'A'} \right)\) có \(ME\) cắt tia \(A'D'\) tại \(F\) suy ra \(\left( {MNPE} \right) \cap A'D' = \left\{ F \right\}\)
Ta có \(AMFD'\) là hình bình hành (do \(MF//AD';AM//D'F\) ) nên \(AM = D'F = \dfrac{1}{2}A'D' \Rightarrow A'F = \dfrac{3}{2}A'D\)
Nên \(F\) không thuộc cạnh \(A'D'\) do đó I) sai.
+ Ta có \(ME//AD'\)(do \(ME\) là đường trung bình \(\Delta DAD'\)) và \(MN//AB\) nên \(\left( {MNP} \right)//\left( {ABC'D'} \right)\) do đó III) đúng.
Chọn D
Câu hỏi 19 :
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, \(M\) là điểm bất kì nằm trong đoạn thẳng \(SC\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\) và song song với mặt phẳng \(\left( {SAB} \right)\). Thiết diện của hình chóp \(S.ABCD\) cắt bởi mặt phẳng \(\left( \alpha \right)\) là hình gì
- A Hình bình hành
- B Hình thang
- C Hình tam giác cân
- D Hình ngũ giác
Đáp án: B
Phương pháp giải:
Dựng các đường thẳng qua \(M\) và song song với các cạnh của tam giác \(SAB\) ta được mặt phẳng \(\left( \alpha \right)\) cần dựng
Từ đó ta xác định thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\)
Lời giải chi tiết:
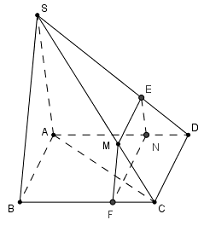
+ Trong mặt phẳng \(\left( {SBC} \right)\)kẻ \(MF//SB\left( {F \in BC} \right)\)
+ Trong mặt phẳng \(\left( {ABCD} \right)\)kẻ \(FN//BA\left( {N \in AD} \right)\)
Từ đó ta có \(\left( {MNF} \right)//\left( {SAB} \right)\)
Trong \(\left( {SCD} \right)\) kẻ \(ME//CD\left( {E \in SD} \right) \Rightarrow ME//CD//FN//AB\) hay \(\left( {MNF} \right) \equiv \left( {MFNE} \right)\)
Suy ra \(\left( \alpha \right) \equiv \left( {MFNE} \right)\)
Ta có \(\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SBC} \right) = MF\\\left( \alpha \right) \cap \left( {SDC} \right) = ME\\\left( \alpha \right) \cap \left( {SAD} \right) = NE\\\left( \alpha \right) \cap \left( {ABCD} \right) = NF\end{array} \right.\) nên thiết diện cắt bởi \(\left( \alpha \right)\) là tứ giác \(MENF\)
Mà \(ME//FN \Rightarrow MENF\) là hình thang.
Chọn B
Câu hỏi 20 :
Cho chóp tứ giác \(S.ABCD\) có đáy là hình bình hành (tham khảo hình vẽ). Gọi \(I,J,K\) lần lượt là trung điểm các cạnh \(SA,SB,SC\). Mệnh đề nào sau đây là mệnh đề sai?
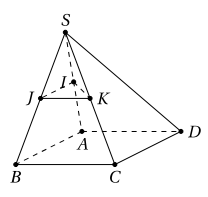
- A \(IJ//CD\)
- B \(SD \cap \left( {IJK} \right) = \emptyset \)
- C \(\left( {IJK} \right) \cap \left( {ACD} \right) = \emptyset \)
- D \(IK//AC\)
Đáp án: B
Phương pháp giải:
Sử dụng tính chất hình bình hành, tính chất đường trung bình của tam giác
Sử dụng cách tìm giao tuyến của hai mặt phẳng, tìm giao điểm của đường thẳng và mặt phẳng.
Lời giải chi tiết:
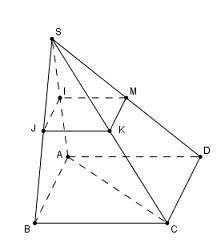
Vì \(ABCD\) là hình bình hành nên \(AB//CD\), lại có \(IJ//AB\) (do \(IJ\) là đường trung bình của tam giác \(SAB\)) nên \(IJ//CD\) hay A đúng.
Lấy \(M\) là trung điểm của \(SD \Rightarrow IJKM\) là hình bình hành nên \(\left( {IJK} \right) \cap SD = \left\{ M \right\}\), do đó B sai.
Vì \(\left\{ \begin{array}{l}IJ//AB\\JK//BC\end{array} \right. \Rightarrow \left( {IJK} \right)//\left( {ACD} \right)\) nên \(\left( {IJK} \right) \cap \left( {ACD} \right) = \emptyset \), do đó C đúng.
+ \(IK//AC\) do \(IK\) là đường trung bình tam giác \(SAC\) nên D đúng.
Chọn B
Câu hỏi 21 :
Cho hình chóp \(S.ABCD\) đáy \(ABCD\) là hình vuông, biết \(AB = a,\,\,\angle SAD = {90^0}\) và tam giác \(SAB\) là tam giác đều. Gọi \(Dt\) là đường thẳng đi qua \(D\) và song song với \(SC,\,\,I\) là giao điểm của \(Dt\) và mặt phẳng\(\left( {SAB} \right)\). Thiết diện của hình chóp \(S.ABCD\) với mặt phẳng \(\left( {AIC} \right)\) có diện tích là:
- A \(\dfrac{{{a^2}\sqrt 5 }}{{16}}\)
- B \(\dfrac{{{a^2}\sqrt 2 }}{4}\)
- C \(\dfrac{{{a^2}\sqrt 7 }}{8}\)
- D \(\dfrac{{11{a^2}}}{{32}}\)
Đáp án: C
Phương pháp giải:
+ Xác định điểm \(I\).
+ Xác định thiết diện.
+ Sử dụng công thức He-rong để tính diện tích tam giác: \({S_{\Delta AEC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \).
Lời giải chi tiết:
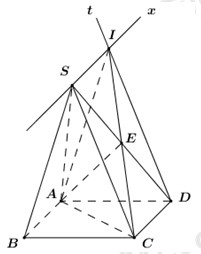
Trong \(\left( {SCD} \right)\) kẻ \(Dt\parallel SC\).
Ta có \(\left\{ \begin{array}{l}S \in \left( {SAB} \right) \cap \left( {SCD} \right)\\\left( {SAB} \right) \supset AB,\,\,\left( {SCD} \right) \supset CD\\AB\parallel CD\,\,\left( {gt} \right)\end{array} \right. \Rightarrow \) Giao tuyến của \(\left( {SAB} \right),\,\,\left( {SCD} \right)\) là đường thẳng đi qua \(S\) và song song với \(AB,\,\,CD\). Trong \(\left( {SAB} \right)\) kẻ \(Sx\parallel AB \Rightarrow \left( {SAB} \right) \cap \left( {SCD} \right) = Sx\).
Trong \(\left( {SCD} \right)\) gọi \(I = Dt \cap Sx\) ta có: \(\left\{ \begin{array}{l}I \in Dt\\I \in Sx \subset \left( {SAB} \right) \Rightarrow I \in \left( {SAB} \right)\end{array} \right. \Rightarrow I = Dt \cap \left( {SAB} \right)\).
Trong \(\left( {SCD} \right)\) gọi \(E = CI \cap SD\), khi đó thiết diện của chóp cắt bởi \(\left( {AIC} \right)\) là tam giác \(AEC\).
\(ABCD\) là hình vuông cạnh \(a \Rightarrow AC = a\sqrt 2 \).
Dễ dàng chứng minh được \(SBAI,\,\,SCDI\) là hình bình hành \( \Rightarrow AI = SB = a,\,\,E\) là trung điểm của \(SD,\,\,IC\).
Tam giác \(SAD\) có \(SA = AD = a,\,\,\angle SAD = {90^0} \Rightarrow \Delta SAD\) vuông cân tại \(A \Rightarrow SD = SA\sqrt 2 = a\sqrt 2 \).
\( \Rightarrow AE = \dfrac{1}{2}SD = \dfrac{{a\sqrt 2 }}{2}\).
Xét tam giác \(IAC\) có:
\(\begin{array}{l}A{E^2} = \dfrac{{A{I^2} + A{C^2}}}{2} - \dfrac{{I{C^2}}}{4} \Leftrightarrow \dfrac{{{a^2}}}{2} = \dfrac{{{a^2} + 2{a^2}}}{2} - \dfrac{{I{C^2}}}{4}\\ \Rightarrow \dfrac{{I{C^2}}}{4} = {a^2} \Leftrightarrow I{C^2} = 4{a^2} \Leftrightarrow IC = 2a \Rightarrow EC = \dfrac{1}{2}IC = a\end{array}\)
Khi đó áp dụng công thức Hê-rông ta có: \({S_{\Delta AEC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \dfrac{{{a^2}\sqrt 7 }}{8}\).
Chọn C.
Câu hỏi 22 :
Cho hai hình bình hành \(ABCD,\,\,ABEF\) nằm trên hai mặt phẳng phân biệt. Gọi M,N lần lượt thuộc đoạn \(AC,\,\,BF\) sao cho \(\dfrac{{AM}}{{AC}} = \dfrac{{BN}}{{BF}}\)( Tham khảo hình vẽ). Đường thẳng \(MN\) song song với mặt phẳng nào sau đây?
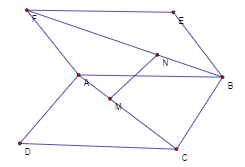
- A \(\left( {ADF} \right)\).
- B \(\left( {DCF} \right)\).
- C \(\left( {ADE} \right)\).
- D \(\left( {BCE} \right)\).
Đáp án: B
Phương pháp giải:
Chứng minh hai mặt phẳng song song rồi suy ra tính chất song song của đường thẳng và mặt phẳng.
Lời giải chi tiết:
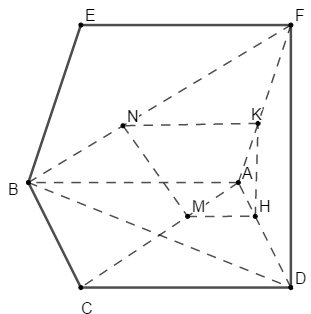
Lấy \(H,\,\,K\) lần lượt trên \(AD,\,\,AF\) sao cho\(\dfrac{{AH}}{{AP}} = \dfrac{{AK}}{{FA}} = \dfrac{{AM}}{{AC}} = \dfrac{{BN}}{{BF}}\).
Tam giác \(AFP\) có \(\dfrac{{AH}}{{AP}} = \dfrac{{AK}}{{FA}}\), áp dụng định lí Ta-lét đảo ta có\(HK\parallel PF\).
Tương tự ta có \(KN\parallel FE\)
Do đó \(\left( {HKN} \right)\parallel \left( {DFE} \right) \Rightarrow \left( {MNKH} \right)\parallel \left( {DFEC} \right) \Rightarrow MN\parallel \left( {DCF} \right)\)
Chọn B.
Câu hỏi 23 :
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh bằng 6cm. Lấy điểm \(M\) trên cạnh \(SA\) sao cho \(SM = 2MA\). Diện tích của hình tứ diện khi cắt bởi mặt phẳng qua \(M\) và song song với \(mp\left( {ABC} \right)\) là:
- A \(4\sqrt 3 c{m^2}.\)
- B \(8\sqrt 3 c{m^2}.\)
- C \(\sqrt 3 c{m^2}.\)
- D
\(16\sqrt 3 c{m^2}.\)
Đáp án: A
Phương pháp giải:
Sử dụng tỉ số và định lí Ta-lét.
Lời giải chi tiết:
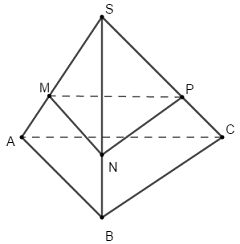
Gọi \(N,\,P\) lần lượt thuộc \(SB,\,\,SC\) sao cho \(\dfrac{{SN}}{{SB}} = \dfrac{{SP}}{{SC}} = \dfrac{{SM}}{{SA}}\).
Khi đó thiết diện của mặt phẳng qua \(M\) song song với \(\left( {ABC} \right)\) là tam giác \(MNP\).
Áp dụng định lí ta-lét trong tam giác SAB có:\(\dfrac{{MN}}{{AB}} = \dfrac{{SM}}{{SA}} = \dfrac{2}{3} = 4\,\,\,\left( {SM = 2MA;SA = 6} \right)\)
Tương tự ta có \(NP = MP = 4cm.\)
Do đó tam giác\(MNP\) là tam giác đều cạnh 4cm.
\( \Rightarrow {S_{MNP}} = \dfrac{{\sqrt 3 }}{4}{.4^2} = 4\sqrt 3 c{m^2}\)
Chọn A.
Câu hỏi 24 :
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Gọi \(O,{O_1}\) lần lượt là tâm của \(ABCD,\,ABEF.\) Lấy \(M\) là trung điểm của \(CD.\) Hỏi khẳng định nào sau đây sai ?
- A \(M{O_1}\) cắt \(\left( {BEC} \right).\)
- B \(O{O_1}//\left( {EFM} \right).\)
- C \(O{O_1}//\left( {BEC} \right).\)
- D \(O{O_1}//\left( {AFD} \right).\)
Đáp án: A
Phương pháp giải:
Sử dụng phương pháp loại đáp án, xét các đáp án đúng, từ đó suy ra đáp án sai.
Lời giải chi tiết:
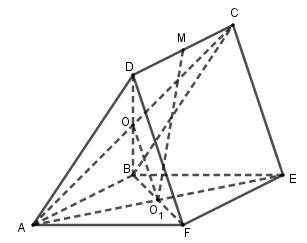
Đáp án B: Dễ thấy \(O{O_1}//DF \subset \left( {EFM} \right)\) nên B đúng.
Đáp án C: \(O{O_1}//CE \subset \left( {BEC} \right)\) nên C đúng.
Đáp án D: \(O{O_1}//DF \subset \left( {AFD} \right)\) nên D đúng.
Ngoài ra A sai vì \(M{O_1}//\left( {BEC} \right)\), thật vậy,
\(O{O_1}//CE\), \(OM//BC\) nên \(\left( {O{O_1}M} \right)//\left( {BCE} \right)\) \( \Rightarrow M{O_1}//\left( {BCE} \right)\).
Chọn A.
Câu hỏi 25 :
Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD,\,\,\,AB//CD,\,\,AB = 2CD.\,\,M\) là một điểm thuộc cạnh \(AD,\,\,\left( \alpha \right)\) là mặt phẳng qua \(M\) và song song với mặt phẳng \(\left( {SAB} \right).\) Biết diện tích thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) bằng \(\dfrac{2}{3}\) diện tích tam giác \(SAB.\) Tính tỉ số \(x = \dfrac{{MA}}{{MD}}.\)
- A \(x = \dfrac{1}{2}.\)
- B \(x = 1.\)
- C \(x = \dfrac{3}{2}.\)
- D \(x = \dfrac{2}{3}.\)
Đáp án: A
Phương pháp giải:
Bước 1. Đặt \(CD = a,\,d\left( {S,AB} \right) = b.\) Sử dụng tính chất của hai đường song song để thiết lập hệ thức giữa độ dài các cạnh.
Bước 2. Tính diện tích của MNPQ, SAB qua \(a,b,x.\)
Bước 3. Sử dụng giả thiết \({S_{MNPQ}} = \dfrac{2}{3}{S_{SAB}}\)để tìm \(x.\)
Lời giải chi tiết:
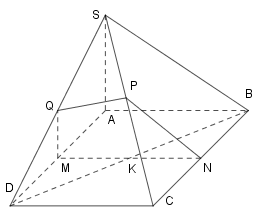
Đặt \(CD = a \Rightarrow AB = 2a.\) Giả sử \(d\left( {S,AB} \right) = b.\)
Ta có thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) là \(MNPQ\,\,\left( {N \in BC,\,P \in SC,\,Q \in SD} \right).\) \( \Rightarrow QP//CD\)
Vì \(MQ//SA\) nên \(\dfrac{{QS}}{{QD}} = \dfrac{{MA}}{{MD}} = x = \dfrac{x}{1} \Rightarrow \dfrac{{QS}}{{QS + QD}} = \dfrac{x}{{x + 1}} = \dfrac{{QS}}{{SD}}.\)
Vì \(QP//DC\) nên \(\dfrac{{QP}}{{DC}} = \dfrac{{QS}}{{SD}} = \dfrac{x}{{x + 1}} \Rightarrow QP = \dfrac{{ax}}{{x + 1}}.\)
Vì \(MN//AD//DC\) nên
\(\begin{array}{l}\,\,\,\,\,\,\dfrac{{MK}}{{AB}} = \dfrac{{MD}}{{AD}} = \dfrac{1}{{x + 1}},\,\,\dfrac{{NK}}{{DC}} = \dfrac{{BN}}{{BC}} = \dfrac{{MA}}{{AD}} \Rightarrow \dfrac{{NK}}{{AB}} = \dfrac{{MA}}{{2AD}} = \dfrac{{xMD}}{{2AD}} = \dfrac{x}{{2\left( {x + 1} \right)}}\\ \Rightarrow \dfrac{{MN}}{{AB}} = \dfrac{{MK + NK}}{{AB}} = \dfrac{{2 + x}}{{2\left( {x + 1} \right)}} \Rightarrow MN = \dfrac{{a\left( {2 + x} \right)}}{{x + 1}}.\end{array}\)
Hơn nữa \(\dfrac{{d\left( {Q,MN} \right)}}{{d\left( {S,AB} \right)}} = \dfrac{{MD}}{{AD}} = \dfrac{1}{{x + 1}} \Rightarrow d\left( {Q,MN} \right) = \dfrac{b}{{x + 1}}.\)
Ta lại có \({S_{SAB}} = \dfrac{1}{2}d\left( {S,AB} \right).AB = ab\) và
\({S_{MNPQ}} = \dfrac{{QP + MN}}{2}d\left( {Q,MN} \right) = \dfrac{1}{2}\left( {\dfrac{{{\rm{ax}}}}{{x + 1}} + \dfrac{{a\left( {x + 2} \right)}}{{x + 1}}} \right)\dfrac{b}{{x + 1}} = \dfrac{{\left( {ax + a} \right)b}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{{a\left( {x + 1} \right)b}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{{ab}}{{x + 1}}.\)
Vì \({S_{MNPQ}} = \dfrac{2}{3}{S_{SAB}} \Rightarrow \dfrac{{ab}}{{x + 1}} = \dfrac{2}{3}ab \Rightarrow 2\left( {x + 1} \right) = 3 \Rightarrow x = \dfrac{1}{2}.\)
Chọn A.
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |