Đề thi giữa kì 2 Toán 6 - Đề số 2 - Cánh diều

Đề bài

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1: Cho 5 điểm trong đó không có ba điểm nào thẳng hàng. Qua hai điểm vẽ được một đường thẳng. Số đường thẳng vẽ được là:

     A. 10                                  B. 9                                    C. 12                                  D. 13

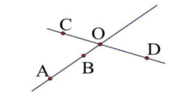
Câu 2: Cho hình vẽ. Trong các khẳng định sau, khẳng định nào là sai?      

     A. Điểm O là giao điểm của hai đường thẳng AB và CD.

     B. Điểm O thuộc đoạn thẳng CD.

     C. Điểm O thuộc đường thẳng AB.

     D. Điểm O thuộc đoạn thẳng AB.

Câu 3: Minh đã khảo sát về địa điểm làm bài tập ở nhà với một số bạn học sinh khối 6 với phiếu hỏi và thu được kết quả như sau:

Chọn biểu đồ thích hợp để biểu diễn số liệu trên.

     A. Biểu đồ cột kép             B. Biểu đồ cột                        C. Biểu đồ hình quạt              D. Biểu đồ tranh

Câu 4: Phân số nào sau đây bằng phân số \(\dfrac{{ - 2}}{5}\)?

     A. \(\dfrac{6}{{ - 15}}\)        B. \( - \dfrac{2}{{10}}\)        C. \(\dfrac{4}{{10}}\)          D. \( - \dfrac{5}{2}\)

Phần II. Tự luận (8 điểm):

Bài 1: (2 điểm) Thực hiện các phép tính:

a) \(\left( {\dfrac{7}{{16}} + \dfrac{{ - 1}}{8} + \dfrac{9}{{32}}} \right):\dfrac{5}{4}\)

b) \(10\dfrac{2}{9} + 2\dfrac{3}{5} - 6\dfrac{2}{9}\)

c) \(\dfrac{{ - 25}}{{30}}.\dfrac{{37}}{{44}} + \dfrac{{ - 25}}{{30}}.\dfrac{{13}}{{44}} + \dfrac{{ - 25}}{{30}}.\dfrac{{ - 6}}{{44}}\)

Bài 2: (1,5 điểm) Tìm x biết:

     a) \( - x - \dfrac{3}{5} =  - \dfrac{1}{{10}}\)                       b) \(\dfrac{2}{3}:x = 2,4 - \dfrac{4}{5}\)        c) \(\dfrac{5}{4}\left( {x - \dfrac{3}{5}} \right) = \dfrac{{ - 1}}{8}\)

Bài 3 (1,5 điểm) Biểu đồ cột kép dưới đây biểu diễn số học sinh giỏi hai môn Toán và Khoa học tự nhiên của các lớp 6A, 6B, 6C, 6D và 6E.

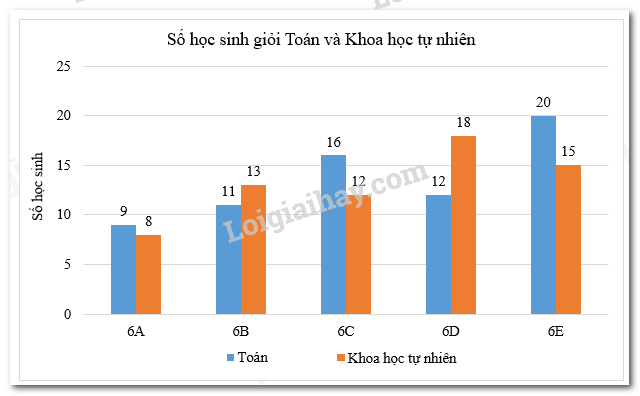
a) Số học sinh giỏi môn Toán của lớp 6D chiếm bao nhiêu phần trăm trong tổng số học sinh giỏi môn Toán của cả 5 lớp?

b) Số học sinh giỏi môn Khoa học tự nhiên của lớp 6A chiếm bao nhiêu phần trăm trong tổng số học sinh giỏi môn Khoa học tự nhiên của cả 5 lớp?

c) Bạn An nói lớp 6E có sĩ số là 35 học sinh. Theo em, bạn An nói có đúng không? Vì sao?

Bài 4: (2,5 điểm) Vẽ đường thẳng xy. Lấy điểm O trên đường thẳng xy, điểm A thuộc tia Ox, điểm B thuộc tia Oy (A và B khác điểm O).

     1. Trong 3 điểm A, O, B điểm nào nằm giữa hai điểm còn lại?

     2. Lấy điểm M nằm giữa hai điểm O và A. Điểm O có nằm giữa hai điểm B và M không?

     3. Nếu OA = 3cm, AB = 6cm thì điểm O có là trung điểm của đoạn thẳng AB không?

Bài 5: (0,5 điểm) Tìm các số nguyên n để biểu thức sau nhận giá trị là số nguyên: \(A = \dfrac{{3n - 4}}{{3 - n}}\).

Lời giải

Phần I: Trắc nghiệm

Câu 1

Phương pháp:

Cứ qua 2 điểm ta vẽ 1 đường thẳng nên với \(n\) điểm không thẳng hàng có tất cả: \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) (đường thẳng)

Cách giải:

Qua 5 điểm trong đó không có 3 điểm nào thẳng hàng ta vẽ được: \(\dfrac{{4.5}}{2} = 10\) (đường thẳng)

Chọn A.

Câu 2

Phương pháp:

Quan sát hình vẽ.

Cách giải:

Điểm O nằm ngoài đoạn thẳng AB.

Vậy D sai.

Chọn D.

Câu 3

Phương pháp:

Sử dụng lý thuyết biểu đồ cột, biểu đồ cột kép.

Cách giải:

Để biểu diễn số liệu trên sử dụng biểu đồ cột.

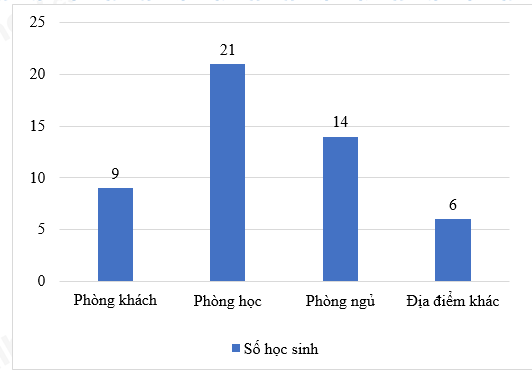
Chọn B.

Câu 4

Kiểm tra tích \(a.d\)và \(b.c\) có bằng nhau hay không.

Cách giải:

Ta có: \(6.5 = \left( { - 2} \right).\left( { - 15} \right)\) nên \(\dfrac{{ - 2}}{5} = \dfrac{6}{{ - 15}}\)

Chọn A.

Phần II: Tự luận

Bài 1

Phương pháp

a) Thực hiện phép tính trong ngoặc trước, ngoài ngoặc sau.

b) Nhóm hai hỗn số có phần phân số giống nhau, sau đó cộng với hỗn số còn lại.

c) Áp dụng tính chất phân phối của phép nhân và phép cộng.

Cách giải:

a) \(\left( {\dfrac{7}{{16}} + \dfrac{{ - 1}}{8} + \dfrac{9}{{32}}} \right):\dfrac{5}{4} = \left( {\dfrac{7}{{16}} + \dfrac{{ - 2}}{{16}} + \dfrac{9}{{32}}} \right):\dfrac{5}{4} = \left( {\dfrac{5}{{16}} + \dfrac{9}{{32}}} \right):\dfrac{5}{4} = \left( {\dfrac{{10}}{{32}} + \dfrac{9}{{32}}} \right):\dfrac{5}{4} = \dfrac{{19}}{{32}}:\dfrac{5}{4} = \dfrac{{19}}{{40}}\)

b) \(10\dfrac{2}{9} + 2\dfrac{3}{5} - 6\dfrac{2}{9} = \left( {10\dfrac{2}{9} - 6\dfrac{2}{9}} \right) + 2\dfrac{3}{5} = 4 + \dfrac{{13}}{5} = \dfrac{{33}}{5}\)

c) \(\dfrac{{ - 25}}{{30}}.\dfrac{{37}}{{44}} + \dfrac{{ - 25}}{{30}}.\dfrac{{13}}{{44}} + \dfrac{{ - 25}}{{30}}.\dfrac{{ - 6}}{{44}} = \dfrac{{ - 25}}{{30}}.\left( {\dfrac{{37}}{{44}} + \dfrac{{13}}{{44}} + \dfrac{{ - 6}}{{44}}} \right) = \dfrac{{ - 5}}{6}.\dfrac{{44}}{{44}} = \dfrac{{ - 5}}{6}\)

Bài 2

Phương pháp

Thực hiện bài toán thứ tự thực hiện phép tính ngược để tìm x.

Cách giải:

a) \( - x - \dfrac{3}{5} =  - \dfrac{1}{{10}}\)

\(\begin{array}{l}x = \dfrac{1}{{10}} - \dfrac{3}{5}\\x = \dfrac{1}{{10}} - \dfrac{6}{{10}}\\x =  - \dfrac{5}{{10}}\\x =  - \dfrac{1}{2}\end{array}\)

Vậy \(x = \dfrac{{ - 1}}{2}.\)

b) \(\dfrac{2}{3}:x = 2,4 - \dfrac{4}{5}\)

\(\begin{array}{l}\dfrac{2}{3}:x = \dfrac{{12}}{5} - \dfrac{4}{5}\\\dfrac{2}{3}:x = \dfrac{8}{5}\\\,\,\,\,\,\,\,x = \dfrac{2}{3}:\dfrac{8}{5}\\\,\,\,\,\,\,\,x = \dfrac{5}{{12}}\end{array}\)

Vậy \(x = \dfrac{5}{{12}}.\)

c) \(\dfrac{5}{4}\left( {x - \dfrac{3}{5}} \right) = \dfrac{{ - 1}}{8}\)

\(\begin{array}{l}x - \dfrac{3}{5} = \dfrac{{ - 1}}{8}:\dfrac{5}{4}\\x - \dfrac{3}{5} = \dfrac{{ - 1}}{{10}}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{{10}} + \dfrac{3}{5}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{{10}} + \dfrac{6}{{10}}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{10}} = \dfrac{1}{2}\end{array}\)

Vậy \(x = \dfrac{1}{2}.\)

Bài 3

Phương pháp:

Sử dụng lý thuyết biểu đồ cột kép.

Cách giải:

a) Tổng số học sinh giỏi môn Toán của cả 5 lớp là:

\(9 + 11 + 16 + 12 + 20 = 68\) (học sinh)

Lớp 6D có \(12\) học sinh giỏi môn Toán chiếm tỉ lệ \(\dfrac{{12}}{{68}} \cdot 100\%  \approx 17,6\% \).

b) Tổng số học sinh giỏi môn Khoa học tự nhiên của cả 5 lớp là:

\(8 + 13 + 12 + 18 + 15 = 66\) (học sinh)

Lớp 6A có \(8\) học sinh giỏi môn Khoa học tự nhiên chiếm tỉ lệ \(\dfrac{8}{{66}} \cdot 100\%  \approx 12,1\% \).

c) An nói chưa chắc đã đúng vì trong lớp còn có thể có những học sinh không phải học sinh giỏi môn Toán, Khoa học tự nhiên và có thể có học sinh vừa là học sinh giỏi môn Toán, vừa là học sinh giỏi môn Khoa học tự nhiên.

Bài 4

Phương pháp:

1. 2. Sử dụng hai tia đối nhau.

3. Chứng minh thêm OA = OB, hết hợp O nằm giữa A và B đã chứng minh ở ý 1.

Cách giải:

1. Vì A thuộc tia Ox, B thuộc tia Oy.

Mà Ox và Oy là hai tia đối nhau nên O nằm giữa A và B.

2. Vì M nằm giữa O và A nên OM cũng chính là tia OA.

Mà OA và OB là hai tia đối nhau nên OM và OB cũng là hai tia đối nhau.

Suy ra O nằm giữa B và M.

3. Vì O nằm giữa A và B nên AO + OB = AB

                                          Hay 3 + OB = 6.

Suy ra OB = 6 – 3 = 3 (cm)

Vì OA = OB (=3cm) và O nằm giữa A và B nên O là trung điểm của AB.

Bài 5

Phương pháp

Phân tích \(A = a + \dfrac{b}{{3 - n}}\), với \(a,\,\,b \in \mathbb{Z}\).

Để \(A \in \mathbb{Z}\) thì \(3 - n \in U\left( b \right)\).

Cách giải:

\(\begin{array}{l}A = \dfrac{{3n - 4}}{{3 - n}} = \dfrac{{3n - 9 + 5}}{{ - n + 3}}\\\,\,\,\,\, = \dfrac{{3n - 9}}{{ - n + 3}} + \dfrac{5}{{ - n + 3}}\\\,\,\,\,\, = \dfrac{{ - 3\left( { - n + 3} \right)}}{{ - n + 3}} + \dfrac{5}{{ - n + 3}}\\\,\,\,\,\, =  - 3 + \dfrac{5}{{ - n + 3}}\end{array}\)

Để A nhận giá trị nguyên thì \( - 3 + \dfrac{5}{{ - n + 3}} \in \mathbb{Z} \Rightarrow \dfrac{5}{{ - n + 3}} \in \mathbb{Z}\)\( \Rightarrow  - n + 3 \in \left\{ { \pm 1; \pm 5} \right\}\)

Ta có bảng giá trị sau:

Vậy \(n \in \left\{ {2;4; - 2;8} \right\}\).