Đề thi, đề kiểm tra Toán lớp 6 - Kết nối tri thức Đề thi học kì 1 Toán 6 Kết nối tri thức

Đề thi học kì 1 Toán 6 - Đề số 16

Tải về

Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên...

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Đề bài

Xem đáp án

Làm đề thi

Tải về

Đề bài

I. Trắc nghiệm

Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1 :

Trong các tập hợp sau, tập hợp nào là tập hợp \({\mathbb{N}^*}\) các số tự nhiên khác 0?

A.

\(\left\{ {1; - 1;2; - 2;3; - 3;...} \right\}\).
B.

\(\left\{ {1;2;3;4;...} \right\}\).
C.

\(\left\{ {0;1;2;3;4;...} \right\}\).
D.

\(\left\{ {0;1;2;3;4;5;6;7;8;9} \right\}\).

Câu 2 :

Trong các số nguyên sau: -2024; -2025; 0; 11. Số nào là số nguyên dương?

A.

-2024.
B.

-2025.
C.

0.
D.

11.

Câu 3 :

Trong các số nguyên sau: -2024; -2025; 0; 11. Số nào là số nguyên lớn nhất?

A.

-2024.
B.

-2025.
C.

0.
D.

11.

Câu 4 :

Khẳng định nào sau đây là sai?

A.

Số đối của -11 là 11.
B.

Số đối của 2024 là -2024.
C.

Số đối của 0 là 0.
D.

Số đối của 100 là +100.

Câu 5 :

Đặc điểm nào sau đây không phải là của hình chữ nhật?

A.

Bốn cạnh bằng nhau.
B.

Hai đường chéo bằng nhau.
C.

Hai cạnh đối song song.
D.

Bốn góc ở bốn đỉnh là góc vuông.

Câu 6 :

Trong các khẳng định sau, khằng định sai là?

A.

(-22) < (-10).
B.

15 < (-4).
C.

(24) > (-25).
D.

(-15) < 0.

Câu 7 :

Thế vận hội đầu tiên diễn ra năm 776 trước Công nguyên. Số âm biểu thị năm diễn ra Thế vận hội đầu tiên là:

A.

776.
B.

767.
C.

-776.
D.

-767.

Câu 8 :

Trong các khẳng định sau, khẳng định nào sai?

A.

Tổng của hai số nguyên dương là một số nguyên dương.
B.

Tích của hai số nguyên khác dấu là một số nguyên âm.
C.

Tổng của hai số nguyên khác dấu là một số nguyên âm.
D.

Kết quả phép trừ số nguyên âm cho số nguyên dương là một số nguyên âm.

Câu 9 :

Dãy nào sau đây chỉ gồm các số nguyên dương:

A.

0; 1; 2; 3; 4; 5.
B.

-1; -4; -5; 2; 4; 5; 0.
C.

-11; 5; -5; 0; -6.
D.

1; 5; 12; 13; 10.

Câu 10 :

Trong các biển báo giao thông sau, biển báo nào có tâm đối xứng?

A.

Biển báo 1.
B.

Biển báo 2.
C.

Biển báo 3.
D.

Biển báo 4.

Câu 11 :

Trong các hình sau đây, hình nào là hình vuông?

A.

Hình (1).
B.

Hình (2).
C.

Hình (3).
D.

Hình (4).

Câu 12 :

Trong các biển báo giao thông sau, biển báo nào có trục đối xứng?

A.

Biển 110a.
B.

Biển 102.
C.

Biển 112.
D.

Biển 123.

II. Tự luận

Câu 1 :

Thực hiện phép tính (tính hợp lí nếu có thể)

a) \(\left( { - 2025} \right) + 2024\)

b) \({5^2}.\left( { - 25} \right) + {5^2}.21\)

c) \(\left( {52 - 41 + 36} \right) - \left( {36 + 52} \right)\)

Câu 2 :

Tìm x, biết:

a) \(x + 6 = 20\)

b) \(54 - \left( {2x + {2^6}} \right) = - 4\)

c) \(x\) là số nguyên và \(29 \vdots x\).

Câu 3 :

Một trường THCS có số học sinh trong khoảng từ 1300 đến 1500 học sinh. Khi tập trung có thể xếp mỗi hàng 40 học sinh hoặc 50 học sinh thì đều vừa đủ hàng. Tính số học sinh của trường đó.

Câu 4 :

a) Vẽ hình thoi ABCD. Tính chu vi của hình thoi có độ dài cạnh là 6cm.

b) Một bức tường hình chữ nhật dài 6m và cao 4m. Biết giá tiền để sơn \(1{m^2}\) tường là 360 000 đồng. Tính số tiền cần phải trả khi sơn bức tường trên.

Câu 5 :

a) Cho 41 số nguyên, trong đó tổng của 5 số bất kì luôn là một số nguyên âm. Chứng tỏ rằng tổng của 41 số đó là một số nguyên âm.

b) Một hộp giấy đựng bỏng ngô gồm bốn mặt xung quanh và một mặt đáy. Biết mỗi mặt xung quanh của hộp có dạng một hình thang cân với độ dài các cạnh đáy lần lượt là 14cm và 12cm, chiều cao là 20cm; đáy hộp có hình vuông cạnh dài 12cm. Hỏi cần bao nhiêu cen-ti-mét vuông giấy bìa để làm một chiếc hộp đựng bỏng ngô đó? (không tính diện tích các mép dán).

Lời giải và đáp án

I. Trắc nghiệm

Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1 :

Trong các tập hợp sau, tập hợp nào là tập hợp \({\mathbb{N}^*}\) các số tự nhiên khác 0?

A.

\(\left\{ {1; - 1;2; - 2;3; - 3;...} \right\}\).
B.

\(\left\{ {1;2;3;4;...} \right\}\).
C.

\(\left\{ {0;1;2;3;4;...} \right\}\).
D.

\(\left\{ {0;1;2;3;4;5;6;7;8;9} \right\}\).

Đáp án : B

Phương pháp giải :

Tập hợp \({\mathbb{N}^*}\) là tập hợp các số tự nhiên khác 0.

Lời giải chi tiết :

Tập hợp \({\mathbb{N}^*}\) là \(\left\{ {1;2;3;4;...} \right\}\).

Đáp án B

Câu 2 :

Trong các số nguyên sau: -2024; -2025; 0; 11. Số nào là số nguyên dương?

A.

-2024.
B.

-2025.
C.

0.
D.

11.

Đáp án : D

Phương pháp giải :

Số nguyên dương là các số tự nhiên lớn hơn 0.

Lời giải chi tiết :

Trong các số trên, chỉ có 11 là số nguyên dương.

Đáp án D

Câu 3 :

Trong các số nguyên sau: -2024; -2025; 0; 11. Số nào là số nguyên lớn nhất?

A.

-2024.
B.

-2025.
C.

0.
D.

11.

Đáp án : D

Phương pháp giải :

So sánh các số để xác định số lớn nhất.

Lời giải chi tiết :

Chỉ có số 11 là số nguyên dương nên 11 là số nguyên lớn nhất.

Đáp án D

Câu 4 :

Khẳng định nào sau đây là sai?

A.

Số đối của -11 là 11.
B.

Số đối của 2024 là -2024.
C.

Số đối của 0 là 0.
D.

Số đối của 100 là +100.

Đáp án : D

Phương pháp giải :

Số đối của số a là –a.

Số đối của 0 là 0.

Lời giải chi tiết :

- Số đối của – 11 là 11 nên A đúng.

- Số đối của 2024 là – 2024 nên B đúng.

- Số đối của 0 là 0 nên C đúng.

- Số đối của 100 là – 100 nên D sai.

Đáp án D

Câu 5 :

Đặc điểm nào sau đây không phải là của hình chữ nhật?

A.

Bốn cạnh bằng nhau.
B.

Hai đường chéo bằng nhau.
C.

Hai cạnh đối song song.
D.

Bốn góc ở bốn đỉnh là góc vuông.

Đáp án : A

Phương pháp giải :

Kiểm tra đặc điểm của hình chữ nhật.

Lời giải chi tiết :

Hình chữ nhật có hai đường chéo bằng nhau, hai cạnh đối song song và bốn góc ở bốn đỉnh là góc vuông.

Bốn cạnh bằng nhau không phải đặc điểm của hình chữ nhật.

Đáp án A

Câu 6 :

Trong các khẳng định sau, khằng định sai là?

A.

(-22) < (-10).
B.

15 < (-4).
C.

(24) > (-25).
D.

(-15) < 0.

Đáp án : B

Phương pháp giải :

- Mọi số nguyên âm đều nhỏ hơn 0.

- Mọi số nguyên âm đều nhỏ hơn số nguyên dương.

- Mọi số nguyên dương đều lớn hơn 0.

- Nếu a, b là hai số nguyên dương và a > b thì − a < − b (Thêm dấu “-” thì đổi dấu “>” thành dấu “<”)

- Nếu a, b là hai số nguyên dương và a < b thì − a > − b

Lời giải chi tiết :

Vì 22 > 10 nên –22 < -10 (A đúng).

Vì 15 là số nguyên dương, -4 là số nguyên âm nên 15 > -4 (B sai).

Vì 24 là số nguyên dương, -25 là số nguyên âm nên 24 > -25 (C đúng).

Vì -15 là số nguyên âm nên -15 < 0 (D đúng).

Đáp án B

Câu 7 :

Thế vận hội đầu tiên diễn ra năm 776 trước Công nguyên. Số âm biểu thị năm diễn ra Thế vận hội đầu tiên là:

A.

776.
B.

767.
C.

-776.
D.

-767.

Đáp án : C

Phương pháp giải :

Đối với năm trước Công nguyên, ta thêm dấu “-“ trước số năm.

Lời giải chi tiết :

Số âm biểu thị năm diễn ra Thế vận hội đầu tiên là: -776.

Đáp án C

Câu 8 :

Trong các khẳng định sau, khẳng định nào sai?

A.

Tổng của hai số nguyên dương là một số nguyên dương.
B.

Tích của hai số nguyên khác dấu là một số nguyên âm.
C.

Tổng của hai số nguyên khác dấu là một số nguyên âm.
D.

Kết quả phép trừ số nguyên âm cho số nguyên dương là một số nguyên âm.

Đáp án : C

Phương pháp giải :

Dựa vào kết quả của phép tính với số nguyên.

Lời giải chi tiết :

- Tổng của hai số nguyên dương là số nguyên dương nên A đúng.

- Tich của hai số nguyên khác dấu là một số nguyên âm (vì dấu “-”. dấu “+” = “-”) nên B đúng.

- Tổng của hai số nguyên khác dấu là một số nguyên âm là khẳng định sai (ví dụ: -2 + 5 = 3 là số nguyên dương) nên C sai.

- Kết quả phép trừ số nguyên âm cho số nguyên dương là một số nguyên âm nên D đúng.

Đáp án C

Câu 9 :

Dãy nào sau đây chỉ gồm các số nguyên dương:

A.

0; 1; 2; 3; 4; 5.
B.

-1; -4; -5; 2; 4; 5; 0.
C.

-11; 5; -5; 0; -6.
D.

1; 5; 12; 13; 10.

Đáp án : D

Phương pháp giải :

Các số nguyên dương là các số lớn hơn 0.

Lời giải chi tiết :

Dãy bao gồm các số nguyên dương là 1; 5; 12; 13; 10.

Đáp án D

Câu 10 :

Trong các biển báo giao thông sau, biển báo nào có tâm đối xứng?

A.

Biển báo 1.
B.

Biển báo 2.
C.

Biển báo 3.
D.

Biển báo 4.

Đáp án : B

Phương pháp giải :

Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.

Lời giải chi tiết :

Hình có tâm đối xứng là Biển báo 2.

Đáp án B

Câu 11 :

Trong các hình sau đây, hình nào là hình vuông?

A.

Hình (1).
B.

Hình (2).
C.

Hình (3).
D.

Hình (4).

Đáp án : A

Phương pháp giải :

Hình vuông là hình có 4 cạnh bằng nhau, 4 góc bằng nhau và bằng \(90^\circ \).

Lời giải chi tiết :

Hình (1) là hình vuông.

Đáp án A

Câu 12 :

Trong các biển báo giao thông sau, biển báo nào có trục đối xứng?

A.

Biển 110a.
B.

Biển 102.
C.

Biển 112.
D.

Biển 123.

Đáp án : B

Phương pháp giải :

Có một đường thẳng d chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau.

Lời giải chi tiết :

Biển 102 có trục đối xứng.

Đáp án B

II. Tự luận

Câu 1 :

Thực hiện phép tính (tính hợp lí nếu có thể)

a) \(\left( { - 2025} \right) + 2024\)

b) \({5^2}.\left( { - 25} \right) + {5^2}.21\)

c) \(\left( {52 - 41 + 36} \right) - \left( {36 + 52} \right)\)

Phương pháp giải :

a) Sử dụng quy tắc cộng hai số nguyên khác dấu.

Để cộng hai số nguyên khác dấu, ta làm như sau:

Bước 1: Bỏ dấu “-” trước số nguyên âm, giữ nguyên số còn lại.

Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn.

Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2, ta có tổng cần tìm.

b) Tính lũy thừa, áp dụng tính chất phân phối của phép nhân với phép cộng để tính.

c) Phá ngoặc sau đó sử dụng tính chất của kết hợp của phép cộng để nhóm.

Lời giải chi tiết :

a) \(\left( { - 2025} \right) + 2024\)

\(\begin{array}{l} = - \left( {2025 - 2024} \right)\\ = - 1\end{array}\)

b) \({5^2}.\left( { - 25} \right) + {5^2}.21\)

\(\begin{array}{l} = 25.\left( { - 25} \right) + 25.21\\ = 25.\left( { - 25 + 21} \right)\\ = 25.\left( { - 4} \right)\\ = - 100\end{array}\)

c) \(\left( {52 - 41 + 36} \right) - \left( {36 + 52} \right)\)

\(\begin{array}{l} = 52 - 41 + 36 - 36 - 52\\ = \left( {52 - 52} \right) + \left( {36 - 36} \right) - 41\\ = 0 + 0 - 41\\ = - 41\end{array}\)

Câu 2 :

Tìm x, biết:

a) \(x + 6 = 20\)

b) \(54 - \left( {2x + {2^6}} \right) = - 4\)

c) \(x\) là số nguyên và \(29 \vdots x\).

Phương pháp giải :

a) Muốn tìm một số hạng trong một tổng ta lấy tổng trừ đi số hạng còn lại.

b) Áp dụng quy tắc chuyển vế để tìm x.

c) \(29 \vdots x\) nên \(x \in \) Ư(29).

Lời giải chi tiết :

a) \(x + 6 = 20\)

\(\begin{array}{l}x = 20 - 6\\x = 14\end{array}\)

Vậy \(x = 14\).

b) \(54 - \left( {2x + {2^6}} \right) = - 4\)

\(\begin{array}{l}54 - \left( {2x + 64} \right) = - 4\\2x + 64 = 54 - \left( { - 4} \right)\\2x + 64 = 58\\2x = 58 - 64\\2x = - 6\\x = \left( { - 6} \right):2\\x = - 3\end{array}\)

Vậy \(x = - 3\).

c) \(x\) là số nguyên và \(29 \vdots x\).

Vì \(29 \vdots x\) nên x là ước của 29.

Mà x là số nguyên nên \(x \in \left\{ { - 29; - 1;1;29} \right\}\).

Câu 3 :

Phương pháp giải :

Gọi số học sinh của trường đó là a (học sinh) \(\left( {a \in {\mathbb{N}^*},1300 \le a \le 1500} \right)\).

Phân tích các số 40, 50 ra thừa số nguyên tố.

Từ đó tìm BCNN(40;50) suy ra BC(40;50).

Kết hợp điều kiện của a để tìm a.

Lời giải chi tiết :

Gọi số học sinh của trường đó là a (học sinh) \(\left( {a \in {\mathbb{N}^*},1300 \le a \le 1500} \right)\).

Vì khi xếp mỗi hàng 40 học sinh hoặc 50 học sinh thì đều vừa đủ hàng nên số học sinh là BC(40;50).

Ta có: \(40 = {2^3}.5\); \(50 = {2.5^2}\).

Suy ra BCNN(40;50) = \({2^3}{.5^2} = 200\), suy ra BC(40;50) = {200; 400;…;1200; 1400; 1600;…}

Mà \(1300 \le a \le 1500\) nên a = 1400.

Vậy trường có 1400 học sinh.

Câu 4 :

a) Vẽ hình thoi ABCD. Tính chu vi của hình thoi có độ dài cạnh là 6cm.

Phương pháp giải :

a) - Thực hiện vẽ hình thoi khi biết độ dài cạnh.

- Sử dụng công thức tính chu vi của hình thoi: 4.cạnh.

b) Tính diện tích bức tường = chiều dài.chiều cao.

Số tiền cần phải trả = giá tiền sơn \(1{m^2}\).diện tích bức tường.

Lời giải chi tiết :

a) * Ta có thể vẽ hình thoi bằng thước và compa như sau:

- Bước 1. Vẽ đoạn thẳng AB = 6cm.

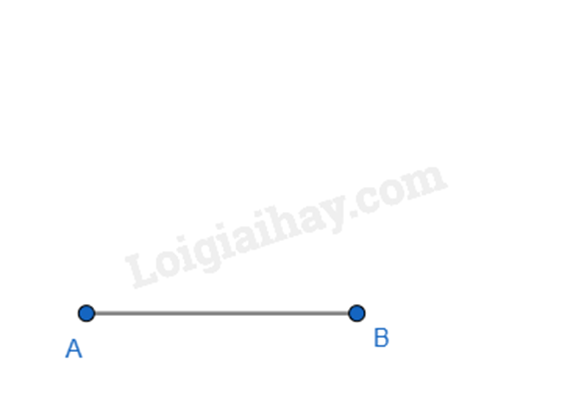
- Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn bán kính AB. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi D là giao điểm của hai đường tròn này.

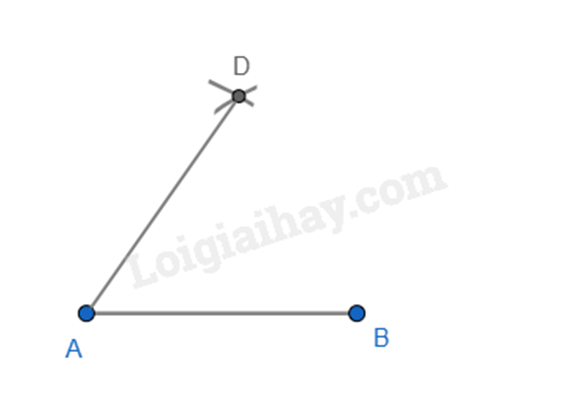
- Bước 3. Lấy D làm tâm, dùng compa vẽ một phần đường tròn bán kính AD. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai đường tròn này.

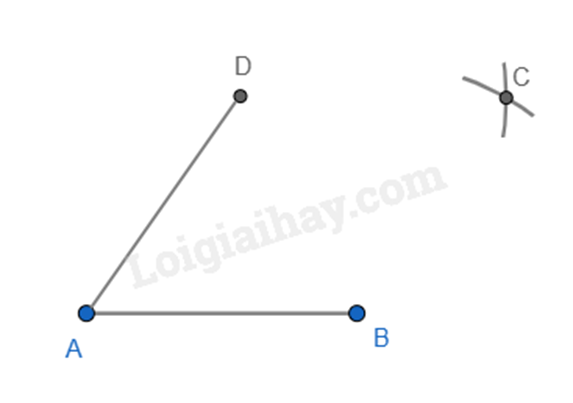
- Bước 4. Dùng thước vẽ các đoạn thẳng BC và CD. Ta được hình thoi ABCD.

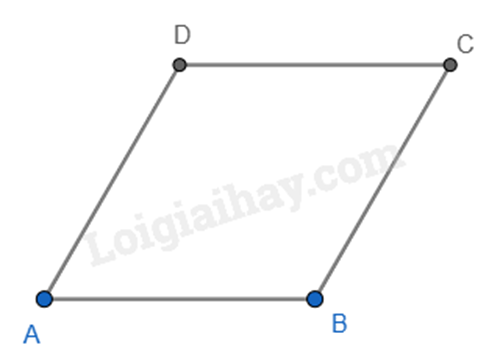
* Chu vi của hình thoi là: 4.6 = 24 (cm).

b) Diện tích bức tường cần sơn là: 6.4 = 24 (\(c{m^2}\))

Số tiền phải trả khi sơn bức tường là: \(360\,000.24 = 8\,640\,000\) (đồng).

Vậy số tiền phải trả khi sơn bức tường là 8 640 000 đồng.

Câu 5 :

a) Cho 41 số nguyên, trong đó tổng của 5 số bất kì luôn là một số nguyên âm. Chứng tỏ rằng tổng của 41 số đó là một số nguyên âm.

Phương pháp giải :

a) Chỉ ra trong 41 số đã cho có ít nhất 1 số nguyên âm.

Chia tổng 40 số còn lại thành 8 nhóm, mỗi nhóm 5 số thì ta được tổng của 8 số nguyên âm là một số nguyên âm. Suy ra tổng của 41 số đã cho là một số nguyên âm.

b) Tính diện tích hình vuông (mặt đáy) và diện tích hình thang cân (bốn mặt xung quanh).

Diện tích hình vuông = cạnh . cạnh.

Diện tích hình thang = \(\frac{1}{2}\) tổng hai đáy . chiều cao.

Diện tích giấy bìa bằng tổng diện tích 4 mặt xung quanh và mặt đáy.

Lời giải chi tiết :

a) Vì trong 41 số nguyên, ta có tổng 5 số nguyên bất kì là một số nguyên âm nên có ít nhất 1 số nguyên âm trong 41 số nguyên.

Gọi số nguyên âm đó là x (x < 0).

Chia tổng 40 số còn lại thành 8 nhóm, mỗi nhóm có 5 số bất kì.

Mà tổng 5 số nguyên bất kì là một số nguyên âm nên tổng mỗi nhóm đều là số nguyên âm. Do đó tổng 8 nhóm là số nguyên âm.

Khi đó tổng của 8 nhóm và số x cũng là số nguyên âm.

Vậy tổng của 41 số nguyên này là số nguyên âm.

b) Diện tích một mặt bên là: \(\frac{1}{2}.\left( {14 + 12} \right).20 = 260\left( {c{m^2}} \right)\)

Diện tích mặt đáy là: \(12.12 = 144\left( {c{m^2}} \right)\)

Diện tích giấy bìa để làm một chiếc hộp đựng bỏng ngô là:

\(144 + 260.4 = 1184\left( {c{m^2}} \right)\)

Vậy cần 1184\(c{m^2}\) giấy bìa để làm một chiếc hộp đựng bỏng ngô.

Đề thi học kì 1 Toán 6 - Đề số 17

Phần trắc nghiệm (2 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 18

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 15 - Kết nối tri thức

Phần trắc nghiệm (3 điểm) Câu 1: Tập hợp các số tự nhiên khác 0 không vượt quá 4 là :

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 14

Phần trắc nghiệm (3 điểm) Câu 1: Cho hình bình hành ABCD có AB = 5 cm, BC = 8 cm thì:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 13 - Kết nối tri thức

Phần trắc nghiệm (3 điểm) Câu 1: Cho tập hợp A = {1; 3; 9; 0; 4; 2}, số phần tử trong tập hợp A là:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 12 - Kết nối tri thức

Phần trắc nghiệm (3 điểm) Câu 1: Cho tập hợp

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 11 - Kết nối tri thức

Phần trắc nghiệm (3 điểm) Câu 1: Tập hợp số tự nhiên được kí hiệu là:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 10

Phần I: Trắc nghiệm (5 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 9

Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 8

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 7