Đề thi, đề kiểm tra Toán lớp 6 - Kết nối tri thức Đề thi giữa kì 2 Toán 6 Kết nối tri thức

Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 6

Tải về

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong cách viết sau, cách viết nào cho ta phân số?

Đề bài

I. Trắc nghiệm
Câu 1 :

Trong cách viết sau, cách viết nào cho ta phân số?

  • A.
    \(\frac{{0,25}}{{ - 3}}\).
  • B.
    \(\frac{5}{0}\).
  • C.
    \(\frac{{25}}{{ - 3}}\).
  • D.
    \(\frac{5}{{4,3}}\).
Câu 2 :

Số đối của phân số \(\frac{5}{{ - 3}}\) là:

  • A.
    \(\frac{5}{3}\).
  • B.
    \(\frac{{ - 5}}{3}\).
  • C.
    \(\frac{3}{{ - 5}}\).
  • D.
    \(\frac{3}{5}\).
Câu 3 :

Phân số \(\frac{{ - 6}}{{15}}\) bằng:

  • A.
    \(\frac{2}{5}\).
  • B.
    \(\frac{{ - 2}}{5}\).
  • C.
    \(\frac{{ - 2}}{{15}}\).
  • D.
    \(\frac{{ - 6}}{5}\).
Câu 4 :

Chọn kết quả đúng:

  • A.
    \(\frac{3}{{10}}\) < \(\frac{3}{7}\).
  • B.
    \(\frac{3}{{10}}\) > \(\frac{3}{7}\).
  • C.
    \(\frac{8}{{15}}\) > \(\frac{3}{5}\).
  • D.
    \(\frac{{ - 8}}{{10}}\) > \(\frac{3}{{74}}\).
Câu 5 :

Chữ số hàng phần trăm của số thập phân -7235,3461 là:

  • A.
    2.
  • B.
    3.
  • C.
    4.
  • D.
    6.
Câu 6 :

Làm tròn số 2315,2345 đến hàng phần trăm ta được số

  • A.
    2315,24.
  • B.
    2315,23.
  • C.
    2315.
  • D.
    2315,20.
Câu 7 :

Số đối của số -7235,346 là

  • A.
    -7235,346.
  • B.
    7235,346.
  • C.
    7235,35.
  • D.
    7235,34.
Câu 8 :

Sắp xếp các số thập phân 7,32; -15,7; -0,9; 6,29 theo thứ tự giảm dần.

  • A.
    7,32; 6,29; -0,9; -15,7.
  • B.
    7,32; 6,29; -15,7; -0,9.
  • C.
    -15,7; 7,32; 6,29; -0,9.
  • D.
    -0,9; -15,7; 6,29; 7,32.
Câu 9 :

Cho hình 1, chọn khẳng định đúng:

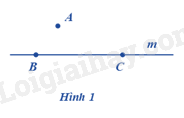
  • A.
    A \( \in \) m.
  • B.
    B \( \in \) m, C \( \in \) m.
  • C.
    A \( \in \) m, C \( \in \) m.
  • D.
    B \( \in \) m, A \( \in \) m.
Câu 10 :

Chọn câu đúng 

  • A.
     Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó không thẳng hàng. 
  • B.
     Nếu ba điểm không cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng.
  • C.
     Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng.
  • D.
     Cả ba đáp án trên đều sai.
Câu 11 :

Cho hình vẽ bên. Hình biểu diễn điểm M là trung điểm của đoạn thẳng AB là:

  • A.
    Hình 3.
  • B.
    Hình 2 và Hình 3.
  • C.
    Hình 1 và Hình 4.
  • D.
    Hình 1 và Hình 3.
Câu 12 :

Trong hình vẽ. Chọn khẳng định đúng

  • A.
    Trong hình có 2 đoạn thẳng.
  • B.
    Trong hình có 1 đoạn thẳng.
  • C.
    Trong hình có 4 đoạn thẳng.
  • D.
    Trong hình có 3 đoạn thẳng.
II. Tự luận
Câu 1 :

1. Sắp xếp dãy phân số \(\frac{1}{2};\frac{1}{4};\frac{1}{6};\;\frac{1}{5}\;\) theo thứ tự từ tăng dần.

2. Tìm x, biết:

a) \(x + 8,5 = 21,7\)

b) \(2,1 + x = - 5,3\)
Câu 2 :

Thực hiện phép tính (Tính hợp lí nếu có thể)

a) \(\frac{{10}}{{11}} + \frac{3}{{11}}:3 - \frac{1}{7}\)

b) \(\frac{{ - 3}}{7} + \frac{5}{{13}} + \frac{3}{7}\)

c) \(\frac{5}{3} \cdot \frac{7}{{25}} + \frac{5}{3} \cdot \frac{{21}}{{25}} - \frac{5}{3} \cdot \frac{7}{{25}}\)
Câu 3 :

Thắng ra siêu thị mua \(3,5\) kg quả bơ sáp, \(2\)kg táo. Giá (chưa tính thuế) của 1kg bơ sáp là \(40\,000\)đồng, 1kg táo là \(25\,000\)đồng

a) Tính tổng số tiền hàng.

b) Khi thanh toán Thắng phải trả thêm thuế VAT (thuế giá trị gia tăng) được tính bằng 10% tổng số tiền hàng. Tính số tiền Thắng phải thanh toán.
Câu 4 :

1. Quan sát hình vẽ và trả lời câu hỏi sau:

a) Kể tên các điểm thuộc đường thẳng a;

b) Điểm nào thuộc cả hai đường thẳng a và b.

2. Vẽ đoạn thẳng AB = 7cm. C là điểm nằm giữa A và B, AC = 3cm. M là trung điểm của BC. Tính BM.
Câu 5 :

So sánh hai phân số sau \({\rm{A}} = \frac{{{{10}^{2022}} + 1}}{{{{10}^{2023}} + 1}};{\rm{B}} = \frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}}\).

Lời giải và đáp án

I. Trắc nghiệm
Câu 1 :

Trong cách viết sau, cách viết nào cho ta phân số?

  • A.
    \(\frac{{0,25}}{{ - 3}}\).
  • B.
    \(\frac{5}{0}\).
  • C.
    \(\frac{{25}}{{ - 3}}\).
  • D.
    \(\frac{5}{{4,3}}\).

Đáp án : C

Phương pháp giải :

Dựa vào khái niệm về phân số.

Lời giải chi tiết :

\(\frac{{0,25}}{{ - 3}}\) không phải phân số vì \(0,25 \notin \mathbb{Z}\).

\(\frac{5}{0}\) không phải phân số vì 0 nằm ở mẫu.

\(\frac{5}{{4,3}}\) không phải phân số vì \(4,3 \notin \mathbb{Z}\).

\(\frac{{25}}{{ - 3}}\) là phân số vì \(25; - 3 \in \mathbb{Z}; - 3 \ne 0\).

Đáp án C.

Câu 2 :

Số đối của phân số \(\frac{5}{{ - 3}}\) là:

  • A.
    \(\frac{5}{3}\).
  • B.
    \(\frac{{ - 5}}{3}\).
  • C.
    \(\frac{3}{{ - 5}}\).
  • D.
    \(\frac{3}{5}\).

Đáp án : A

Phương pháp giải :

Số đối của phân số \(\frac{a}{b}\) là phân số \( - \frac{a}{b}\).

Lời giải chi tiết :

Số đối của phân số \(\frac{5}{{ - 3}}\) là \(\frac{5}{3}\).

Đáp án A.

Câu 3 :

Phân số \(\frac{{ - 6}}{{15}}\) bằng:

  • A.
    \(\frac{2}{5}\).
  • B.
    \(\frac{{ - 2}}{5}\).
  • C.
    \(\frac{{ - 2}}{{15}}\).
  • D.
    \(\frac{{ - 6}}{5}\).

Đáp án : B

Phương pháp giải :

Sử dụng quy tắc rút gọn phân số.

Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu – (nếu có)

Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất vừa tìm được, ta có phân số tối giản cần tìm

Lời giải chi tiết :

Ta có: \(\frac{{ - 6}}{{15}} = \frac{{ - 6:3}}{{15:3}} = \frac{{ - 2}}{5}\).

Đáp án B.

Câu 4 :

Chọn kết quả đúng:

  • A.
    \(\frac{3}{{10}}\) < \(\frac{3}{7}\).
  • B.
    \(\frac{3}{{10}}\) > \(\frac{3}{7}\).
  • C.
    \(\frac{8}{{15}}\) > \(\frac{3}{5}\).
  • D.
    \(\frac{{ - 8}}{{10}}\) > \(\frac{3}{{74}}\).

Đáp án : A

Phương pháp giải :

Dựa vào quy tắc so sánh phân số

Lời giải chi tiết :

So sánh \(\frac{3}{{10}}\) với \(\frac{3}{7}\): \(\frac{3}{{10}} = \frac{{3.7}}{{10.7}} = \frac{{21}}{{70}}\); \(\frac{3}{7} = \frac{{3.10}}{{7.10}} = \frac{{30}}{{70}}\). Vì \(21 < 30\) nên \(\frac{{21}}{{70}} < \frac{{30}}{{70}}\). Do đó \(\frac{3}{{10}} < \frac{3}{7}\).

Nên A đúng, B sai.

\(\frac{8}{{15}} < \frac{9}{{15}} = \frac{3}{5}\) nên C sai.

\(\frac{{ - 8}}{{10}} < 0 < \frac{3}{{74}}\) nên D sai.

Đáp án A.

Câu 5 :

Chữ số hàng phần trăm của số thập phân -7235,3461 là:

  • A.
    2.
  • B.
    3.
  • C.
    4.
  • D.
    6.

Đáp án : C

Phương pháp giải :

Dựa vào kiến thức về số thập phân.

Lời giải chi tiết :

Chữ số hàng phần trăm của số thập phân -7235,3461 là 4.

Đáp án C.

Câu 6 :

Làm tròn số 2315,2345 đến hàng phần trăm ta được số

  • A.
    2315,24.
  • B.
    2315,23.
  • C.
    2315.
  • D.
    2315,20.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về làm tròn số.

Lời giải chi tiết :

Làm tròn số 2315,2345 đến hàng phần trăm ta được số 2315,23.

Đáp án B.

Câu 7 :

Số đối của số -7235,346 là

  • A.
    -7235,346.
  • B.
    7235,346.
  • C.
    7235,35.
  • D.
    7235,34.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về số đối: Hai số đối nhau thì tổng của chúng bằng 0.

Lời giải chi tiết :

Số đối của số -7235,346 là 7235,346.

Đáp án B.

Câu 8 :

Sắp xếp các số thập phân 7,32; -15,7; -0,9; 6,29 theo thứ tự giảm dần.

  • A.
    7,32; 6,29; -0,9; -15,7.
  • B.
    7,32; 6,29; -15,7; -0,9.
  • C.
    -15,7; 7,32; 6,29; -0,9.
  • D.
    -0,9; -15,7; 6,29; 7,32.

Đáp án : A

Phương pháp giải :

Dựa vào quy tắc so sánh hai số thập phân.

Lời giải chi tiết :

Ta chia các số thập phân thành hai nhóm

+ Nhóm 1 (các số lớn hơn 0): 7,32; 6,29

Ta có: 7,32 > 6,29.

+ Nhóm 2 (các số nhỏ hơn 0): -15,7; -0,9.

Vì 0,9 < 15,7 nên – 0,9 > - 15,7.

Sắp xếp các số đó theo thứ tự giảm dần, ta được:

7,32; 6,29; -0,9; -15,7.

Đáp án A.

Câu 9 :

Cho hình 1, chọn khẳng định đúng:

  • A.
    A \( \in \) m.
  • B.
    B \( \in \) m, C \( \in \) m.
  • C.
    A \( \in \) m, C \( \in \) m.
  • D.
    B \( \in \) m, A \( \in \) m.

Đáp án : B

Phương pháp giải :

Quan sát hình vẽ để xác định.

Lời giải chi tiết :

Quan sát hình vẽ ta thấy điểm A không thuộc m, điểm B, C thuộc m nên ta có:

\(A \notin m;b \in m;c \in m\). Vậy đáp án đúng là B.

Đáp án B.

Câu 10 :

Chọn câu đúng 

  • A.
     Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó không thẳng hàng. 
  • B.
     Nếu ba điểm không cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng.
  • C.
     Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng.
  • D.
     Cả ba đáp án trên đều sai.

Đáp án : C

Phương pháp giải :

Dựa vào kiến thức về ba điểm thẳng hàng.

Lời giải chi tiết :

Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng nên C đúng.

Đáp án C.

Câu 11 :

Cho hình vẽ bên. Hình biểu diễn điểm M là trung điểm của đoạn thẳng AB là:

  • A.
    Hình 3.
  • B.
    Hình 2 và Hình 3.
  • C.
    Hình 1 và Hình 4.
  • D.
    Hình 1 và Hình 3.

Đáp án : D

Phương pháp giải :

Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu đoạn thẳng. Trung điểm của đoạn thẳng còn gọi là điểm chính giữa của đoạn thẳng.

Lời giải chi tiết :

Hình 1 và hình 3 biểu diễn điểm M là trung điểm của AB.

Đáp án D.

Câu 12 :

Trong hình vẽ. Chọn khẳng định đúng

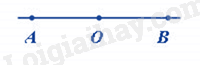
  • A.
    Trong hình có 2 đoạn thẳng.
  • B.
    Trong hình có 1 đoạn thẳng.
  • C.
    Trong hình có 4 đoạn thẳng.
  • D.
    Trong hình có 3 đoạn thẳng.

Đáp án : D

Phương pháp giải :

Dựa vào kiến thức về đoạn thẳng.

Lời giải chi tiết :

Hình vẽ có 3 đoạn thẳng, đó là: AO, OB, AB.

Đáp án D.

II. Tự luận
Câu 1 :

1. Sắp xếp dãy phân số \(\frac{1}{2};\frac{1}{4};\frac{1}{6};\;\frac{1}{5}\;\) theo thứ tự từ tăng dần.

2. Tìm x, biết:

a) \(x + 8,5 = 21,7\)

b) \(2,1 + x = - 5,3\)
Phương pháp giải :

1. Dựa vào quy tắc so sánh các phân số cùng tử số.

2. Sử dụng quy tắc tính với số thập phân để tìm x.

Lời giải chi tiết :

1. Vì 2 < 4 < 5 < 6 nên \(\frac{1}{2} > \frac{1}{4} > \frac{1}{5} > \;\frac{1}{6}\)

2. 

a) x + 8,5 = 21,7

x = 21,7 – 8,5

x = 13,2

Vậy x = 13,2.

b) \(2,1 + x = - 5,3\)

x = - 5,3 – 2,1

x = -7,4

Vậy x = -7,4.

Câu 2 :

Thực hiện phép tính (Tính hợp lí nếu có thể)

a) \(\frac{{10}}{{11}} + \frac{3}{{11}}:3 - \frac{1}{7}\)

b) \(\frac{{ - 3}}{7} + \frac{5}{{13}} + \frac{3}{7}\)

c) \(\frac{5}{3} \cdot \frac{7}{{25}} + \frac{5}{3} \cdot \frac{{21}}{{25}} - \frac{5}{3} \cdot \frac{7}{{25}}\)
Phương pháp giải :

Dựa vào quy tắc tính với phân số.

Lời giải chi tiết :

a) \(\frac{{10}}{{11}} + \frac{3}{{11}}:3 - \frac{1}{7}\)\( = \frac{{10}}{{11}} + \frac{1}{{11}} - \frac{1}{7}\)\( = \frac{{11}}{{11}} - \frac{1}{7}\)\( = 1 - \frac{1}{7}\)\( = \frac{6}{7}\)

b) \(\frac{{ - 3}}{7} + \frac{5}{{13}} + \frac{3}{7}\)\( = \left( {\frac{{ - 3}}{7} + \frac{3}{7}} \right) + \frac{5}{{13}}\)\( = 0 + \frac{5}{{13}}\)\( = \frac{5}{{13}}\)

c) \(\frac{5}{3} \cdot \frac{7}{{25}} + \frac{5}{3} \cdot \frac{{21}}{{25}} - \frac{5}{3} \cdot \frac{7}{{25}}\)\( = \frac{5}{3}.\left( {\frac{7}{{25}} + \frac{{21}}{{25}} - \frac{7}{{25}}} \right)\)\( = \frac{5}{3}.\frac{{21}}{{25}}\)\( = \frac{7}{5}\)

Câu 3 :

Thắng ra siêu thị mua \(3,5\) kg quả bơ sáp, \(2\)kg táo. Giá (chưa tính thuế) của 1kg bơ sáp là \(40\,000\)đồng, 1kg táo là \(25\,000\)đồng

a) Tính tổng số tiền hàng.

b) Khi thanh toán Thắng phải trả thêm thuế VAT (thuế giá trị gia tăng) được tính bằng 10% tổng số tiền hàng. Tính số tiền Thắng phải thanh toán.
Phương pháp giải :

a) Tính tổng số tiền hàng.

b) Tính số tiền thuế giá trị gia tăng.

Số tiền Thắng phải thanh toán bằng tổng số tiền hàng và tiền thuế VAT.

Lời giải chi tiết :

a) Tổng số tiền hàng Thắng đã mua là:

\(3,5.40\,000 + 2.25\,000 = 140\,000 + 50\,000 = 190000\) (đồng)

b) Số tiền thuế giá trị gia tăng VAT là:

\(190000.\frac{{10}}{{100}} = 19\,000\) (đồng)

Số tiền Thắng phải thanh toán là:

\(190\,000 + 19\,000 = 209\,000\) (đồng)

Vậy số tiền hàng là 190 000 đồng; số tiền Thắng phải thanh toán là 209 000 đồng.

Câu 4 :

1. Quan sát hình vẽ và trả lời câu hỏi sau:

a) Kể tên các điểm thuộc đường thẳng a;

b) Điểm nào thuộc cả hai đường thẳng a và b.

2. Vẽ đoạn thẳng AB = 7cm. C là điểm nằm giữa A và B, AC = 3cm. M là trung điểm của BC. Tính BM.
Phương pháp giải :

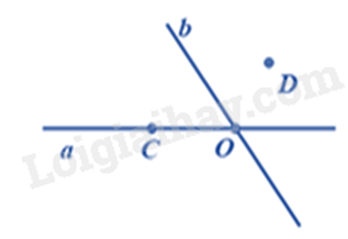
1. Quan sát hình vẽ để trả lời.

2. Sử dụng kiến thức về trung điểm của một đoạn thẳng.

Lời giải chi tiết :

1. 

a) Điểm C, O thuộc đường thẳng a.

b) Điểm O thuộc đường thẳng a và b.

2. 

Ta có \(C\) nằm giữa \(A\) và \(B\) nên \(AC + BC = AB\)

Hay \(BC = AB - AC = 7 - 3 = 4cm\).

Vì \(M\) là trung điểm \(BC\) nên \(BM = \frac{{BC}}{2} = \frac{4}{2} = 2(cm)\).

Vậy BM = 2cm.

Câu 5 :

So sánh hai phân số sau \({\rm{A}} = \frac{{{{10}^{2022}} + 1}}{{{{10}^{2023}} + 1}};{\rm{B}} = \frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}}\).
Phương pháp giải :

Lấy 1 – A; 1 – B.

So sánh 1 – A và 1 – B từ đó ta so sánh được A và B.

Lời giải chi tiết :

+) \(1 - A = 1 - \frac{{{{10}^{2022}} + 1}}{{{{10}^{2023}} + 1}} = \frac{{{{10}^{2023}} + 1}}{{{{10}^{2023}} + 1}} - \frac{{{{10}^{2022}} + 1}}{{{{10}^{2023}} + 1}} = \frac{{{{10}^{2023}} - {{10}^{2022}}}}{{{{10}^{2023}} + 1}} = \frac{{{{10}^{2022}}.9}}{{{{10}^{2023}} + 1}}\)

+) \(1 - B = 1 - \frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}} = \frac{{{{10}^{2022}} + 1}}{{{{10}^{2022}} + 1}} - \frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}} = \frac{{{{10}^{2022}} - {{10}^{2021}}}}{{{{10}^{2022}} + 1}} = \frac{{{{10}^{2021}}.9}}{{{{10}^{2022}} + 1}}\)

+) Để so sánh \(1 - A\) và \(1 - B\) ta so sánh \(\frac{{10}}{{{{10}^{2023}} + 1}}\) và \(\frac{1}{{{{10}^{2022}} + 1}}\)

\(\frac{1}{{{{10}^{2022}} + 1}} = \frac{{10}}{{{{10}^{2023}} + 10}} < \frac{{10}}{{{{10}^{2023}} + 1}}\)

Suy ra \(1 - B < 1 - A\)

Suy ra \(A < B\).

Vậy A < B.

 

Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 7

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong cách viết sau, cách viết nào cho ta phân số?

Xem chi tiết
Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 8

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong các cách viết sau, cách viết nào không phải là phân số?

Xem chi tiết
Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 9

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Phân số nghịch đảo của phân số \(\frac{1}{3}\) là

Xem chi tiết
Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 10

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Phân số nào dưới đây không biểu diễn phần tô màu cam trong hình bên:

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 5 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 4 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 3 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 2 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 1 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

>> Học trực tuyến lớp 6 chương trình mới trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 6 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store