Đề thi, đề kiểm tra Toán lớp 6 - Kết nối tri thức Đề thi giữa kì 2 Toán 6 Kết nối tri thức

Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 9

Tải về

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Phân số nghịch đảo của phân số \(\frac{1}{3}\) là

Đề bài

I. Trắc nghiệm
Câu 1 :

Phân số nghịch đảo của phân số \(\frac{1}{3}\) là

  • A.
    \(3\).
  • B.
    \( - \frac{1}{3}\).
  • C.
    \( - 3\).
  • D.
    \(1\).
Câu 2 :

Khẳng định nào sau đây đúng?

  • A.
    \( - \frac{2}{7} > \frac{1}{7}\).
  • B.
    \(\frac{2}{7} < \frac{1}{7}\).
  • C.
    \(\frac{2}{7} =  - \frac{1}{7}\).
  • D.
    \(\frac{2}{7} > \frac{1}{7}\).
Câu 3 :

Cho \(\frac{3}{4}x = 1\frac{2}{3}\). Kết quả giá trị x là:

  • A.
    \(\frac{{20}}{9}\).
  • B.
    \(\frac{5}{4}\).
  • C.
    \(\frac{{29}}{{12}}\).
  • D.
    \(\frac{{11}}{{12}}\).
Câu 4 :

Cho a, b, m là các số nguyên, m khác 0. Tổng \(\frac{a}{m} + \frac{b}{m}\) bằng

  • A.
    \(\frac{{a + b}}{{m + m}}\).
  • B.
    \(\frac{{a + b}}{{m.m}}\).
  • C.
    \(\frac{{a + b}}{m}\).
  • D.
    \(a + b\).
Câu 5 :

Trong các cách viết sau, cách viết nào cho ta một số thập phân âm?

  • A.
    \(2,37\).
  • B.
    \(\frac{2}{3}\).
  • C.
    \(1\frac{5}{{26}}\).
  • D.
    \( - 3,25\).
Câu 6 :

Số đối của số thập phân -3,7 là:

  • A.
    -3,7.
  • B.
    3,7.
  • C.
    -7,3.
  • D.
    7,3.
Câu 7 :

Làm tròn số 12,643 đến hàng đơn vị ta được số

  • A.
    12,6.
  • B.
    13.
  • C.
    12.
  • D.
    12,64.
Câu 8 :

Tỉ số phần trăm của 1 và 4 là

  • A.

    \(75\% .\)

  • B.
    \(50\% .\)
  • C.

    \(25\% .\)

  • D.
    \(14\% .\)
Câu 9 :

Cho hình vẽ: Điểm thuộc đường thẳng d là:

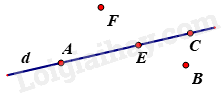
  • A.
    Điểm E và B.
  • B.
    Điểm C và F.
  • C.
    Điểm F và B.
  • D.
    Điểm A, E và C.
Câu 10 :

Cho hình vẽ, chọn khẳng định đúng trong các khẳng định sau:

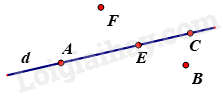
  • A.
    Ba điểm A, F, E thẳng hàng.
  • B.
    Ba điểm A, B, C thẳng hàng.
  • C.
    Ba điểm A, E, C thằng hàng.
  • D.
    Ba điểm E, B, C thẳng hàng.
Câu 11 :

Hình nào sau đây vẽ đoạn thẳng \(AB\)?

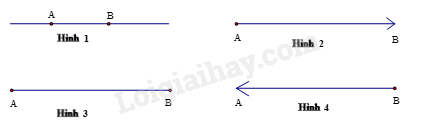
  • A.
    Hình 2.
  • B.
    Hình 3.
  • C.
    Hình 4.
  • D.
    Hình 1.
Câu 12 :

Cho \(I\) là trung điểm của đoạn thẳng \(AB\). Biết \(AB = 10cm\), số đo của đoạn thẳng \(IB\) là

  • A.
    4cm.
  • B.
    5cm.
  • C.
    6cm.
  • D.
    20cm.
II. Tự luận
Câu 1 :

Thực hiện các phép tính sau (tính hợp lý nếu có thể).

a) \(\frac{{ - 2}}{{11}} + \frac{{ - 9}}{{11}}\)

b) \(\frac{1}{2} - \frac{{ - 3}}{4}\)

c) \(\frac{{12}}{{11}} - \frac{{ - 7}}{{19}} + \frac{{12}}{{19}}\)

d) \(\frac{{ - 5}}{7} \cdot \frac{2}{{11}} + \frac{{ - 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7}\)
Câu 2 :

Tìm \(x\), biết:

a) \(2,5 + x = 3,75\)

b) \(6,72 - x = ( - 12,6) + 6,3\)
Câu 3 :

Lớp 6A có 42 học sinh xếp loại kết quả học tập trong học kỳ I  bao gồm ba loại: Tốt, khá và đạt. Số học sinh tốt chiếm \(\frac{1}{7}\) số học sinh cả lớp, số học sinh khá  bằng \(\frac{2}{3}\) số học sinh còn lại.

a) Tính số học sinh mỗi loại của lớp?

b) Tính tỉ số phần trăm của số học sinh tốt và khá so với số học sinh cả lớp?
Câu 4 :

Trên tia Bx lấy hai điểm A và C sao cho BA = 2cm , BC = 3cm

a) Trong ba điểm C, A, B điểm nào nằm giữa hai điểm còn lại? Tính AC?

b) Trên tia đối của tia Bx lấy điểm O sao cho BO = BC = B có phải là trung điểm của OC không? Vì sao?
Câu 5 :

Tính \(S = \left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)\left( {1 - \frac{1}{{{4^2}}}} \right)\left( {1 - \frac{1}{{{5^2}}}} \right)\left( {1 - \frac{1}{{{6^2}}}} \right)...\left( {1 - \frac{1}{{{{99}^2}}}} \right)\).

Lời giải và đáp án

I. Trắc nghiệm
Câu 1 :

Phân số nghịch đảo của phân số \(\frac{1}{3}\) là

  • A.
    \(3\).
  • B.
    \( - \frac{1}{3}\).
  • C.
    \( - 3\).
  • D.
    \(1\).

Đáp án : A

Phương pháp giải :

Phân số nghịch đảo của phân số \(\frac{a}{b}\) là \(\frac{b}{a}\) \(\left( {\frac{a}{b}.\frac{b}{a} = 1} \right)\)

Lời giải chi tiết :

Phân số nghịch đảo của phân số \(\frac{1}{3}\) là \(3\).

Đáp án A.

Câu 2 :

Khẳng định nào sau đây đúng?

  • A.
    \( - \frac{2}{7} > \frac{1}{7}\).
  • B.
    \(\frac{2}{7} < \frac{1}{7}\).
  • C.
    \(\frac{2}{7} =  - \frac{1}{7}\).
  • D.
    \(\frac{2}{7} > \frac{1}{7}\).

Đáp án : D

Phương pháp giải :

So sánh hai phân số cùng mẫu.

Lời giải chi tiết :

Ta có \( - 2 < 1\) nên \(\frac{{ - 2}}{7} < \frac{1}{7}\) (A sai).

\(2 > 1\) nên \(\frac{2}{7} > \frac{1}{7}\) (B sai).

\(2 \ne  - 1\) nên \(\frac{2}{7} \ne  - \frac{1}{7}\) (C sai)

\(2 > 1\) nên \(\frac{2}{7} > \frac{1}{7}\) (D đúng)

Đáp án D.

Câu 3 :

Cho \(\frac{3}{4}x = 1\frac{2}{3}\). Kết quả giá trị x là:

  • A.
    \(\frac{{20}}{9}\).
  • B.
    \(\frac{5}{4}\).
  • C.
    \(\frac{{29}}{{12}}\).
  • D.
    \(\frac{{11}}{{12}}\).

Đáp án : A

Phương pháp giải :

Sử dụng quy tắc tính với phân số.

Lời giải chi tiết :

\(\begin{array}{l}\frac{3}{4}x = 1\frac{2}{3}\\\frac{3}{4}x = \frac{5}{3}\\x = \frac{5}{3}:\frac{3}{4}\\x = \frac{{20}}{9}\end{array}\)

Đáp án A.

Câu 4 :

Cho a, b, m là các số nguyên, m khác 0. Tổng \(\frac{a}{m} + \frac{b}{m}\) bằng

  • A.
    \(\frac{{a + b}}{{m + m}}\).
  • B.
    \(\frac{{a + b}}{{m.m}}\).
  • C.
    \(\frac{{a + b}}{m}\).
  • D.
    \(a + b\).

Đáp án : C

Phương pháp giải :

Dựa vào quy tắc cộng hai phân số cùng mẫu.

Lời giải chi tiết :

\(\frac{a}{m} + \frac{b}{m} = \frac{{a + b}}{m}\)

Đáp án C.

Câu 5 :

Trong các cách viết sau, cách viết nào cho ta một số thập phân âm?

  • A.
    \(2,37\).
  • B.
    \(\frac{2}{3}\).
  • C.
    \(1\frac{5}{{26}}\).
  • D.
    \( - 3,25\).

Đáp án : D

Phương pháp giải :

Số thập phân âm là số nhỏ hơn 0.

Lời giải chi tiết :

Số thập phân âm là \( - 3,25\).

Đáp án D.

Câu 6 :

Số đối của số thập phân -3,7 là:

  • A.
    -3,7.
  • B.
    3,7.
  • C.
    -7,3.
  • D.
    7,3.

Đáp án : B

Phương pháp giải :

Số đối của số a là – a.

Lời giải chi tiết :

Số đối của số thập phân -3,7 là 3,7.

Đáp án B.

Câu 7 :

Làm tròn số 12,643 đến hàng đơn vị ta được số

  • A.
    12,6.
  • B.
    13.
  • C.
    12.
  • D.
    12,64.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức làm tròn số.

Lời giải chi tiết :

Làm tròn số 12,643 đến hàng đơn vị ta được số 13.

Đáp án B.

Câu 8 :

Tỉ số phần trăm của 1 và 4 là

  • A.

    \(75\% .\)

  • B.
    \(50\% .\)
  • C.

    \(25\% .\)

  • D.
    \(14\% .\)

Đáp án : C

Phương pháp giải :

Tỉ số phần trăm của a và b là \(\frac{a}{b}.100\% \).

Lời giải chi tiết :

Tỉ số phần trăm của 1 và 4 là: \(\frac{1}{4}.100\%  = 25\% \).

Đáp án C.

Câu 9 :

Cho hình vẽ: Điểm thuộc đường thẳng d là:

  • A.
    Điểm E và B.
  • B.
    Điểm C và F.
  • C.
    Điểm F và B.
  • D.
    Điểm A, E và C.

Đáp án : D

Phương pháp giải :

Quan sát hình vẽ để trả lời.

Lời giải chi tiết :

Điểm thuộc đường thẳng d là A, E, C.

Đáp án D.

Câu 10 :

Cho hình vẽ, chọn khẳng định đúng trong các khẳng định sau:

  • A.
    Ba điểm A, F, E thẳng hàng.
  • B.
    Ba điểm A, B, C thẳng hàng.
  • C.
    Ba điểm A, E, C thằng hàng.
  • D.
    Ba điểm E, B, C thẳng hàng.

Đáp án : C

Phương pháp giải :

Ba điểm cùng thuộc một đường thẳng thì thẳng hàng.

Lời giải chi tiết :

Vì A, E, C nằm trên đường thẳng d nên chúng thẳng hàng.

Đáp án C.

Câu 11 :

Hình nào sau đây vẽ đoạn thẳng \(AB\)?

  • A.
    Hình 2.
  • B.
    Hình 3.
  • C.
    Hình 4.
  • D.
    Hình 1.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về đoạn thẳng.

Lời giải chi tiết :

Hình vẽ đoạn thẳng AB là hình 3.

Đáp án B.

Câu 12 :

Cho \(I\) là trung điểm của đoạn thẳng \(AB\). Biết \(AB = 10cm\), số đo của đoạn thẳng \(IB\) là

  • A.
    4cm.
  • B.
    5cm.
  • C.
    6cm.
  • D.
    20cm.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về trung điểm của đoạn thẳng.

Lời giải chi tiết :

Vì I là trung điểm của AB nên AI = IB = \(\frac{1}{2}\)AB = \(\frac{1}{2}\).10 = 5(cm).

Đáp án B.

II. Tự luận
Câu 1 :

Thực hiện các phép tính sau (tính hợp lý nếu có thể).

a) \(\frac{{ - 2}}{{11}} + \frac{{ - 9}}{{11}}\)

b) \(\frac{1}{2} - \frac{{ - 3}}{4}\)

c) \(\frac{{12}}{{11}} - \frac{{ - 7}}{{19}} + \frac{{12}}{{19}}\)

d) \(\frac{{ - 5}}{7} \cdot \frac{2}{{11}} + \frac{{ - 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7}\)
Phương pháp giải :

Dựa vào quy tắc tính với phân số.

Lời giải chi tiết :

a) \(\frac{{ - 2}}{{11}} + \frac{{ - 9}}{{11}} = \frac{{ - 2 + ( - 9)}}{{11}} = \frac{{ - 11}}{{11}} = - 1\)

b) \(\frac{1}{2} - \frac{{ - 3}}{4} = \frac{{1.2}}{{2.2}} - \frac{{ - 3}}{4} = \frac{2}{4} - \frac{{ - 3}}{4} = \frac{{2 - ( - 3)}}{4} = \frac{5}{4}.\)

c) \(\frac{{12}}{{11}} - \frac{{ - 7}}{{19}} + \frac{{12}}{{19}}\) \( = \frac{{12}}{{11}} + \frac{7}{{19}} + \frac{{12}}{{19}}\) \( = \frac{{12}}{{11}} + \left( {\frac{7}{{19}} + \frac{{12}}{{19}}} \right)\) \( = \frac{{12}}{{11}} + 1\) \( = \frac{{12}}{{11}} + \frac{{11}}{{11}}\) \( = \frac{{23}}{{11}}.\)

d) \(\frac{{ - 5}}{7} \cdot \frac{2}{{11}} + \frac{{ - 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7} = \frac{{ - 5}}{7}\left( {\frac{2}{{11}} + \frac{9}{{11}}} \right) + \frac{5}{7} = \frac{{ - 5}}{7} \cdot 1 + \frac{5}{7} = 0\)

Câu 2 :

Tìm \(x\), biết:

a) \(2,5 + x = 3,75\)

b) \(6,72 - x = ( - 12,6) + 6,3\)
Phương pháp giải :

Dựa vào quy tắc tính với số thập phân.

Lời giải chi tiết :

a) \(2,5 + x = 3,75\)

\(x = 3,75 - 2,5\)

\(x = 1,25\)

Vậy \(x = 1,25\)

b) \(6,72 - x = ( - 12,6) + 6,3\)

\(6,72 - x =  - 6,3\)

\(x = 6,72 + 6,3\)

\(x = 13,02\)

Vậy x = 13,02.

Câu 3 :

Lớp 6A có 42 học sinh xếp loại kết quả học tập trong học kỳ I  bao gồm ba loại: Tốt, khá và đạt. Số học sinh tốt chiếm \(\frac{1}{7}\) số học sinh cả lớp, số học sinh khá  bằng \(\frac{2}{3}\) số học sinh còn lại.

a) Tính số học sinh mỗi loại của lớp?

b) Tính tỉ số phần trăm của số học sinh tốt và khá so với số học sinh cả lớp?
Phương pháp giải :

a) Tính số học sinh tốt, học sinh khá theo số học sinh cả lớp

Số học sinh đạt bằng số học sinh cả lớp trừ đi số học sinh tốt và học sinh khá.

b) Tính tổng số học sinh tốt và khá : số học sinh cả lớp . 100%.

Lời giải chi tiết :

a) Số học sinh tốt là: \(42.\frac{1}{7} = 6\)( học sinh)

Số học sinh khá là: \((42 - 6).\frac{2}{3} = 24\)(học sinh)

Số học sinh đạt là : \(42 - 6 - 24 = 12\)(học sinh)

b) Tỉ số % giữa học sinh tốt và khá so với cả lớp là:

\(\frac{{6 + 24}}{{42}}.100\%  = 71,4\% \)

Vậy số học sinh tốt, khá, đạt lần lượt là 6; 24; 12 học sinh.

Tỉ số phần trăm giữa học sinh tốt và khá so với cả lớp là 71,4%.

Câu 4 :

Trên tia Bx lấy hai điểm A và C sao cho BA = 2cm , BC = 3cm

a) Trong ba điểm C, A, B điểm nào nằm giữa hai điểm còn lại? Tính AC?

b) Trên tia đối của tia Bx lấy điểm O sao cho BO = BC = B có phải là trung điểm của OC không? Vì sao?
Phương pháp giải :

a) So sánh BA với BC để xác định điểm nằm giữa.

b) Chứng minh B nằm giữa O và C và BO = BC nên B là trung điểm của OC.

Lời giải chi tiết :

a) Trên tia Bx ta có BA = 2cm, BC = 3cm vì 2 < 3 nên BA < BC, vậy, A nằm giữa B và C.

Khi đó ta có : BA + AC = BC suy ra \(AC = BC - BA\) suy ra \(AC = 3 - 2 = 1\)

Vậy AC = 1cm.

b) Ta có O thuộc tia đối của tia Bx, nên O và C nằm khác phía đối với B hay B nằm giữa O và C.

Khi đó: OB + BC = OC. (1)

Mà theo đề bài: BO = BC = 3cm (2)

Từ (1) và (2), suy ra B là trung điểm của OC.

Câu 5 :

Tính \(S = \left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)\left( {1 - \frac{1}{{{4^2}}}} \right)\left( {1 - \frac{1}{{{5^2}}}} \right)\left( {1 - \frac{1}{{{6^2}}}} \right)...\left( {1 - \frac{1}{{{{99}^2}}}} \right)\).
Phương pháp giải :

Rút gọn A, biến đổi các phân số trong A để rút gọn.

Lời giải chi tiết :

\(\begin{array}{l}S = \left( {1 - \frac{1}{4}} \right).\left( {1 - \frac{1}{9}} \right).\left( {1 - \frac{1}{{16}}} \right).\left( {1 - \frac{1}{{25}}} \right)\left( {1 - \frac{1}{{36}}} \right)...\left( {1 - \frac{1}{{9901}}} \right)\\ = \frac{3}{4} \cdot \frac{8}{9} \cdot \frac{{15}}{{16}} \cdot \frac{{24}}{{25}} \cdot \frac{{35}}{{36}} \cdots \frac{{9800}}{{99}}\\ = \frac{{1.3}}{{2.2}} \cdot \frac{{2.4}}{{3.3}} \cdot \frac{{3.5}}{{4.4}} \cdot \frac{{4.6}}{{5.5}} \cdot \frac{{5.7}}{{6.6}} \cdots \frac{{98.100}}{{99.99}}\\ = \frac{{1.2.3.4.5...98}}{{2.3.4.5.6...99}} \cdot \frac{{3.4.5.6.7...100}}{{2.3.4.5.6...99}}\\ = \frac{1}{{99}} \cdot \frac{{100}}{2}\\ = \frac{{50}}{{99}} \cdot \end{array}\)

Vậy \(S = \frac{{50}}{{99}}\).

Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 10

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Phân số nào dưới đây không biểu diễn phần tô màu cam trong hình bên:

Xem chi tiết
Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 8

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong các cách viết sau, cách viết nào không phải là phân số?

Xem chi tiết
Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 7

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong cách viết sau, cách viết nào cho ta phân số?

Xem chi tiết
Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 6

Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong cách viết sau, cách viết nào cho ta phân số?

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 5 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 4 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 3 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 2 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết
Đề thi giữa kì 2 Toán 6 - Đề số 1 - Kết nối tri thức

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

>> Học trực tuyến lớp 6 chương trình mới trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 6 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store