Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Ôn tập chương II: Hàm số và đồ thị
Đề kiểm tra 45 phút - Đề số 3 - Chương 2 - Đại số 7
Giải Đề kiểm tra 45 phút - Đề số 3 - Chương 2 - Đại số 7
Đề bài
Bài 1: Phân tích số 90 thành tổng của 3 số và ba số đó tỉ lệ nghịch với 3;4;6. Tìm ba số đó.
Bài 2: Số học sinh giỏi, khá, trung bình của khối 7 tỉ lệ thuận với 2; 5 ;6. Tổng số học sinh giỏi và khá nhiều hơn số học sinh trung bình là 45 em. Tính số học sinh giỏi, khá, trung bình của mỗi khối 7.
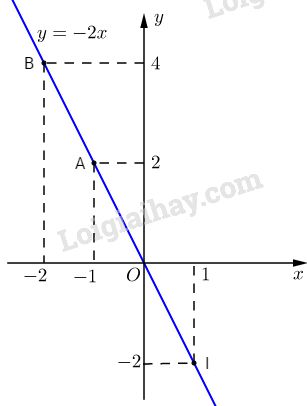
Bài 3: Cho hàm số \(y = - 2x\)
a) Vẽ đồ thị của hàm số.
b) Điểm \(M(0;-2)\) có thuộc đồ thị của hàm số hay không?
c) Chứng tỏ rằng ba điểm \(O; A(-1;2)\) và \(B(-2;4)\) thẳng hàng.
LG bài 1
Phương pháp giải:
Sử dụng tính chất dãy tỉ số bằng nhau \(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{{a + c + e}}{{b + d + f}}\)
Lời giải chi tiết:
Gọi x, y, z là ba số cần tìm. Ta có \(x + y + z = 90\)
Vì x, y, z tỉ lệ nghịch với 3,4,6 nên ta có \(3x = 4y = 6z\)
\( \Rightarrow {x \over {{1 \over 3}}} = {y \over {{1 \over 4}}} = {z \over {{1 \over 6}}} = {{x + y + z} \over {{1 \over 3} + {1 \over 4} + {1 \over 6}}} = {{90} \over {{3 \over 4}}} = 120\)
\( \Rightarrow x = {{120} \over 3} = 40;y = {{120} \over 4} = 30;\)\(\;z = {{120} \over {60}} = 20.\)
Vậy ba số cần tìm là : 40 ; 30 ; 20.
LG bài 2
Phương pháp giải:
Sử dụng tính chất dãy tỉ số bằng nhau \(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{{a + c -e}}{{b + d - f}}\)
Lời giải chi tiết:
Gọi x, y, z là số học sinh giỏi, khá, trung bình cần tìm ; \(x,y,z \in {\mathbb N^*}\) .
Theo điều kiện của bài toán : Tổng số học sinh giỏi, khá nhiều hơn số học sinh trung bình là 45 em nên : \(x + y - z = 45\)
Vì x, y, z tỉ lệ thuận với 2 ; 5 ; 6 nên ta có : \({x \over 2} = {y \over 5} = {z \over 6} \)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\({x \over 2} = {y \over 5} = {z \over 6} = {{x + y - z} \over {2 + 5 - 6}}\)\(=\frac{45}1=45.\)
\(\Rightarrow x = 45.2=90;\)\(y =45.5= 225;z =45.6= 270\)
Vậy Số học sinh giỏi , khá, trung bình lần lượt là 90 ; 225 ; 270 (em)
LG bài 3
Phương pháp giải:
Đồ thị hàm số \(y = ax (a ≠ 0)\) là đường thẳng đi qua gốc toạ độ và \(A(1;a)\)
Điểm \(M(x_0;y_0)\) thuộc đồ thị hàm số \(y=ax\) nếu \(y_0=ax_0\)
Thay tọa độ các điểm A, B, O vào hàm số \(y=-2x\) để chỉ ra 3 điểm thẳng hàng.
Lời giải chi tiết:
a) Đồ thị của hàm số \(y = -2x\) là đường thẳng qua gốc tọa độ O và điểm \(I(1 ;-2)\) (xem hình vẽ).
b) Thế tọa độ của M :\({x_M} = 0;{y_M} = - 2\) vào công thức \(y = -2x\), ta được :
\(2=(-2).0\) (sai)
Vậy M không thuộc đồ thị.
c) Thế tọa độ của A: \({x_A} = - 1;{y_A} = 2\) vào công thức \(y = 2x\) ta được:
\(-2 = (-2).(-1)\) ( luôn đúng).
Vậy A nằm trên đồ thị của hàm số \(y = -2x.\)
Tương tự đối với điểm B. Theo trên O cũng là điểm thuộc đồ thị và đồ thị là đường thẳng nên có có thể nói O ; A ; B thẳng hàng.
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 45 phút - Đề số 4 - Chương 2 - Đại số 7
- Đề kiểm tra 45 phút - Đề số 5 - Chương 2 - Đại số 7
- Đề kiểm tra 45 phút - Đề số 2 - Chương 2 - Đại số 7
- Đề kiểm tra 45 phút - Đề số 1 - Chương 2 - Đại số 7
- Lý thuyết Ôn tập chương 2. Hàm số và đồ thị
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
