Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Ôn tập chương II: Hàm số và đồ thị
Đề kiểm tra 45 phút - Đề số 1 - Chương 2 - Đại số 7
Giải Đề kiểm tra 45 phút - Đề số 1 - Chương 2 - Đại số 7
Đề bài
Bài 1: Có ba loại tiền mệnh giá 2000 đồng; 5000 đồng và 10 000 đồng gồm 16 tờ. Biết rằng tổng giá trị của mỗi loại đều bằng nhau. Hỏi mỗi loại tiền có bao nhiêu tờ?
Bài 2: Vẽ đồ thị của hàm số \(y = -2x\) . Điểm \(M(-5;10)\) có thuộc đồ thị của hàm số hay không? Chứng tỏ ba điểm O;\(A(-1;2)\) và \(B(2;-4)\) thẳng hàng.
Bài 3: Cho tam giác ABC , biết rằng số đo ba góc A;B;C tỉ lệ thuận với \({1 \over 2};{1 \over 3};{1 \over 6}\) .Tìm số đo của ba góc A,B,C.
Bài 4 : Cho hàm số \(y = f(x) = mx\). Tìm m biết \(f\left( {{1 \over 2}} \right) = 2\).
LG bài 1
Phương pháp giải:
Sử dụng tính chất dãy tỉ số bằng nhau \(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{{a + c + e}}{{b + d + f}}\)
Lời giải chi tiết:
Gọi x, y, z là số tờ tiền của loại tiền mệnh giá 2000 đồng và 5000 đồng và 10 000 đồng (\(x,y,z \in {\mathbb N^*}\))
Vì có tất cả 16 tờ tiền nên ta có: \(x + y + z = 16\)
Vì tổng giá trị của mỗi loại bằng nhau nên ta có :
\(\eqalign{ & 2000x = 5000y = 10000z \cr & \Rightarrow {{2000x} \over {10000}} = {{5000y} \over {10000}} = {{10000z} \over {10000}} \cr} \)
\( \Rightarrow {x \over 5} = {y \over 2} = {z \over 1} = {{x + y + z} \over {5 + 2 + 1}}=\frac{16}8=2\)(Tính chất của dãy tỉ số bằng nhau)
\(\Rightarrow x = 5.2 = 10;y = 2.2 = 4;\)\(\;z = 1.2 = 2\)
Vậy loại tiền 2000 đồng có 10 tờ, 5000 đồng có 4 tờ ; 10 000 đồng có 2 tờ.
LG bài 2
Phương pháp giải:
Đồ thị hàm số \(y = ax (a ≠ 0)\) là đường thẳng đi qua gốc toạ độ và \(A(1;a)\)
Thay tọa độ các điểm A, B, C vào hàm số \(y=-2x\) để chỉ ra 3 điểm thẳng hàng.
Lời giải chi tiết:
Đồ thị của hàm số \(y = -2x\) có đường thẳng qua gốc tọa độ O và điểm \(P(1 ;-2)\)
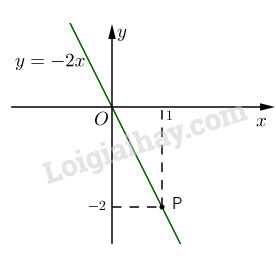
Thay tọa độ của điểm \(M(-5 ;10)\) vào hàm số \(y = -2x \); với \(x = -5 ; y = 10.\)
Ta có : \(10 = (-2).(-5)\) hay \(10 = 10\) (luôn đúng).
Vậy M thuộc đồ thị hàm số \(y = -2x.\)
Tương tự, ta được A,B thuộc đồ thị hàm số \(y = -2x\) (là đường thẳng)
Vậy O, A, B thẳng hàng.
LG bài 3
Phương pháp giải:
Sử dụng tính chất dãy tỉ số bằng nhau \(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{{a + c + e}}{{b + d + f}}\)
Lời giải chi tiết:
Trong tam giác ABC, ta có \(\widehat A + \widehat B + \widehat C = {180^0}.\)
Vì \(\widehat A,\widehat B,\widehat C\) tỉ lệ thuận với \({1 \over 2};{1 \over 3};{1 \over 6}\) .
\({{\widehat A} \over {{1 \over 2}}} = {{\widehat B} \over {{1 \over 3}}} = {{\widehat C} \over {{1 \over 6}}} = {{\widehat A + \widehat B + \widehat C} \over {{1 \over 2} + {1 \over 3} + {1 \over 6}}} = {{{{180}^0}} \over 1}\)
\( \Rightarrow \widehat A = {{{{180}^0}} \over 2} = {90^0};\widehat B = {{{{180}^0}} \over 3} = {60^0};\)\(\;\widehat C = {{{{180}^0}} \over 6} = {30^0}\)
Vậy \(\widehat A = {90^0};\widehat B = {60^0};\widehat C = {30^0}.\)
LG bài 4
Phương pháp giải:
Thay \(x=\frac {1}2;y=2\) vào hàm số để tìm m.
Lời giải chi tiết:
Ta có: \(\displaystyle f(x)=mx\) nên \(\displaystyle f\left( {{1 \over 2}} \right)=m. {{1 \over 2}} \)
Suy ra:
\(\displaystyle f\left( {{1 \over 2}} \right) = 2 \Rightarrow 2 = m. {{1 \over 2}} \Rightarrow m = 2:\frac{1}{2}= 4.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 45 phút - Đề số 2 - Chương 2 - Đại số 7
- Đề kiểm tra 45 phút - Đề số 3 - Chương 2 - Đại số 7
- Đề kiểm tra 45 phút - Đề số 4 - Chương 2 - Đại số 7
- Đề kiểm tra 45 phút - Đề số 5 - Chương 2 - Đại số 7
- Lý thuyết Ôn tập chương 2. Hàm số và đồ thị
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
