 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Ôn tập chương I: Đường thẳng vuông góc. Đường thẳng son..
Ôn tập chương I: Đường thẳng vuông góc. Đường thẳng son..
Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 1 - Hình học 7
Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 1 - Hình học 7
Đề bài
Bài 1: Cho hình vẽ. Biết a // b và \(\widehat A = {90^o}\), \(\widehat {AHB} = {110^o}\). Tính \(\widehat B\)
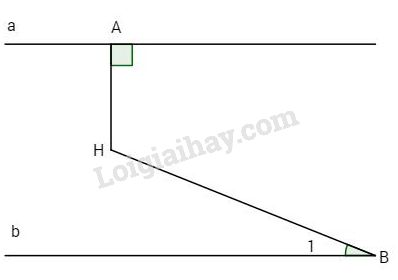
Bài 2: Cho hình vẽ.
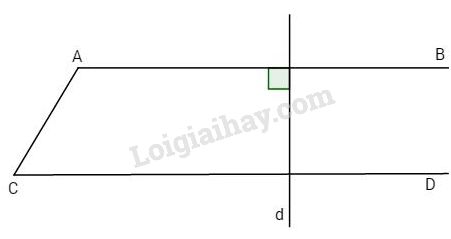
Biết \(\widehat {BAC} + \widehat {ACD} = {180^o};\,d \bot AB\)
Chứng minh: \(d \bot CD\)
Bài 3: Cho hình vẽ. Biết
\(\eqalign{ & \widehat {xAB} = {150^o}; \cr & AB \bot BC; \cr & \widehat {yBC} = {120^o}. \cr} \)
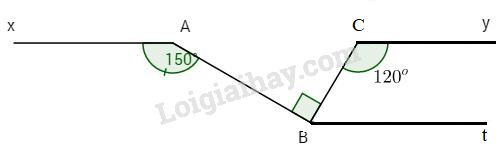
Chứng minh Ax // Cy.
Phương pháp giải:
+\(\left\{ {\begin{array}{*{20}{c}}{a//b}\\{b//c}\end{array}} \right. \Rightarrow a//c\)
+\(\left\{ {\begin{array}{*{20}{c}}{a \bot b}\\{b//c}\end{array}} \right. \Rightarrow a \bot c\)
Nếu 1 đường thẳng cắt hai đường thẳng song song thì:
a) Các cặp góc so le trong bằng nhau.
b) Các cặp góc đồng vị bằng nhau.
c) Các cặp góc trong cùng phía bù nhau
LG bài 1
Lời giải chi tiết:
Kẻ tia Ht nằm giữa hai tia HA và HB và Ht // a.
Vì \(\widehat A = {90^o}\) (giả thiết)
\( \Rightarrow \widehat {tHB} = \widehat {AHB} - \widehat {AHt} = {110^o} - {90^o} = {20^o}.\) \( \Rightarrow HA \bot a\). Lại có Ht // a
\( \Rightarrow Ht \bot HA\) hay \(\widehat {AHt} = {90^o}.\)
\( \Rightarrow \widehat {tHB} = \widehat {AHB} - \widehat {AHt} = {110^o} - {90^o} = {20^o}.\)
Vì a // b (giả thiết)
\(\left. {\matrix{{\text{Vì }a//b\left( \text{giả thiết } \right)} \hfill \cr {Ht//a} \hfill \cr} } \right\} \Rightarrow Ht//b\) (hai đường thẳng phân biệt cùng song song với đường thứ ba thì chúng song song với nhau).
\( \Rightarrow \widehat {{B_1}} = \widehat {tHB} = {20^o}\)(cặp góc so le trong).
Câu 3
Lời giải chi tiết:
Ta có \(\widehat {BAC}\) và \(\widehat {ACD}\) là hai góc trong cùng phía
Mà \(\widehat {BAC} + \widehat {ACD} = {180^o}\)(giả thiết)
\( \Rightarrow AB//CD\) mà \(AB \bot d \Rightarrow d \bot CD\)
(Nếu một đường thẳng vuông góc với một trong hai đường song song thì nó vuông góc cả với đường thẳng kia).
LG bài 3
Lời giải chi tiết:
Kẻ tia Bt sao cho tia BC nằm trong góc Abt và Bt // Cy.
Ta có \(\widehat C + \widehat {CBt} = {180^o}\) (cặp góc trong cùng phía)
\( \Rightarrow {120^o} + \widehat {CBt} = {180^o} \Rightarrow \widehat {CBt} = {180^o} - {120^o} = {60^o}.\)
Tia BC nằm giữa hai tia BA và Bt nên
\(\widehat {ABt} = \widehat {ABC} + \widehat {CBt} = {90^o} + {60^o} = {150^o}.\)
Hai góc \(\widehat {xAB}\) và \(\widehat {ABt}\) là hai góc so le trong, mà \(\widehat {xAB} = \widehat {ABt} = {150^o}\)
\( \Rightarrow \) Ax // Bt. Lại có Bt // Cy \(\Rightarrow\) Ax // Cy (hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song).
Loigiaihay.com
- Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 1 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 1 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 1 - Hình học 7
- Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 1 - Hình học 7
- Lý thuyết Ôn tập chương 1. Đường thẳng vuông góc. Đường thẳng song song
>> Xem thêm












Danh sách bình luận