Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 7
Đề bài
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}.\) Gọi Om, On lần lượt là các tia phân giác của \(\widehat {xOy}\) và \(\widehat {yOz}.\)
a) Tính số đo góc \(\widehat {mOn}.\)
b) Vẽ góc \(\widehat {zOy'}\) là góc đối đỉnh với góc \(\widehat {xOy}\) và Om’ là tia đối của tia Om. Chứng minh Om’ là tia phân giác của góc \(\widehat {y'Oz}\) và On là tia phân giác cuả góc \(\widehat {mOm'}.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề bù có tổng bằng \(180^0\)
Lời giải chi tiết
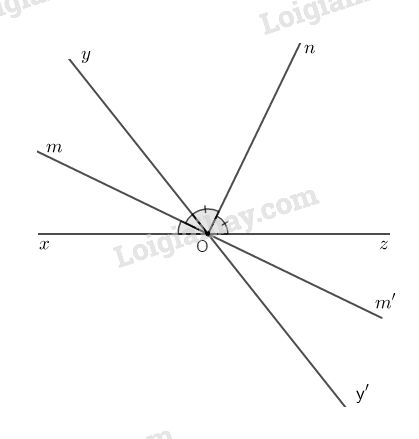
a) Ta có Om là tia phân giác của \(\widehat {xOy}\) nên
\(\widehat {xOm} = \widehat {yOm} =\dfrac {1 }{2}\widehat {xOy}.\)
Tương tự: \(\widehat {mOm'} + \widehat {nOm'} = {180^o}\)
\(\Rightarrow \widehat {nOm'} = \widehat {mOn} = {90^o},\) \(\widehat {yOn} = \widehat {zOn} = \dfrac{1 }{ 2}\widehat {yOz}\)
Mà \(\widehat {xOy} + \widehat {yOz} = {180^o}\)
\( \Rightarrow \widehat {xOm} = \widehat {yOn} = {90^o}\) hay \(\widehat {mOn} = {90^o}.\)
b) Ta có \(\widehat {zOy'} = \widehat {xOy}\) (đối đỉnh) và Om’ là hai tia đối của tia Om nên \(\widehat {xOm}\)và \(\widehat {zOm'}\), \(\widehat {yOm}\)và \(\widehat {y'Om'}\) là các cặp góc đối đỉnh.
\( \Rightarrow \widehat {zOm'} = \widehat {y'Om'},\) chứng tỏ Om’ là hai phân giác của góc \(\widehat {zOy'}\).
Theo chứng minh trên ta có \(\widehat {mOn} = {90^o}\) mà Om’ và Om là hai tia đối nhau nên \(\widehat {mOn} + \widehat {nOm'} = {180^o}\)
\(\Rightarrow \widehat {nOm'} = \widehat {mOn} = {90^o},\)
Chứng tỏ On là hai tia phân giác của \(\widehat {mOm'}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 1 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 1 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 1 - Hình học 7
- Bài 10 trang 83 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
