Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội

Đề bài

Bài 1. (2 điểm) Giải các hệ phương trình sau:

a) \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}2x + y = 2\\3x - y =  - 7\end{array}\end{array}} \right.\)

b) \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\frac{1}{{x - y}} + \frac{4}{y} =  - \frac{{17}}{{15}}\\\frac{5}{{x - y}} - \frac{6}{y} = 3\end{array}\end{array}} \right.\) với \(x \ne y;y \ne 0\).

Bài 2. (2 điểm)

1) Cho phương trình: \(3x - 4y = m - 1\) (\(m\) là tham số).

a) Tìm \(m\) để cặp số \((2; - 1)\) là một nghiệm của phương trình.

b) Với \(m\) tìm được ở câu a, hãy biểu diễn tập nghiệm của phương trình trên mặt phẳng tọa độ \(Oxy\).

2) Cô Nguyệt có hai khoản đầu tư với lãi suất là 6% và 8% mỗi năm. Cô thu được tiền lãi từ hai khoản đầu tư đó là 150 triệu đồng mỗi năm. Nếu coi \(x\) (triệu đồng) là khoản đầu tư với lãi suất 6% và \(y\) (triệu đồng) là khoản đầu tư với lãi suất 8%, với \(x > 0;y > 0\). Hãy viết phương trình bậc nhất hai ẩn cho hai khoản đầu tư của cô Nguyệt.

3) Cho tam giác ABC có \(\hat A = 30^\circ \), \(AB = 3\) cm, \(AC = 4\) cm. Tính diện tích của tam giác ABC.

Bài 3. (2 điểm) Bạn Dũng đi xe đạp từ địa điểm \(A\) đến địa điểm \(B\), bạn Trang cũng đi xe đạp, nhưng từ địa điểm \(B\) đến địa điểm \(A\). Hai bạn gặp nhau khi bạn Dũng đã đi được \(1\) giờ 30 phút, còn bạn Trang đã đi được \(2\) giờ. Một lần khác hai bạn cũng đi từ hai địa điểm như thế và trên cùng tuyến đường nhưng khởi hành đồng thời, sau \(1\) giờ 15 phút thì còn cách nhau 10,5 km. Tính vận tốc của mỗi bạn, biết rằng đoạn đường AB dài 38 km.

Bài 4. (3,5 điểm)

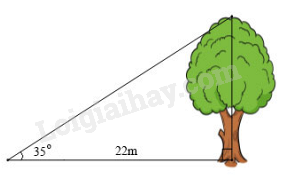
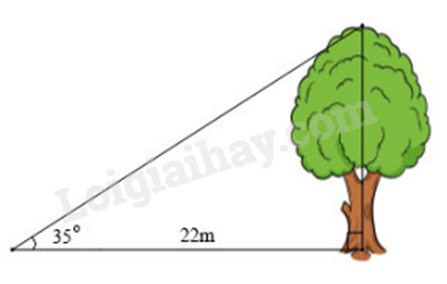
1) Bóng trên mặt đất của một cây dài 22 m. Tính chiều cao của cây (làm tròn kết quả đến hàng đơn vị), biết rằng tia nắng mặt trời tạo với mặt đất một góc \(35^\circ \).

2) Cho tam giác nhọn ABC\((\)AB < AC) có các đường cao BD, CE cắt nhau tại \(H\) (\(D \in AC\), \(E \in AB\)).

a) Chứng minh \(AE \cdot BD = AD \cdot CE\).

b) Qua \(B\) kẻ đường thẳng vuông góc với AB tại \(B\) và qua \(C\) kẻ đường thẳng vuông góc với AC tại \(C\), hai đường thẳng này cắt nhau tại \(K\). Chứng minh tứ giác BHCK là hình bình hành và \(\widehat {BAH} = \widehat {CAK}\).

c) Gọi \(O\) là giao điểm của BC và HK. Đoạn thẳng AH cắt ED tại \(M\) và đoạn thẳng AK cắt BC tại \(N\). Chứng minh AO đi qua trung điểm \(I\) của đoạn thẳng MN.

Bài 5. (0,5 điểm) Cho các số x, y, z khác \(0\) thỏa mãn: \(x + y + z = 1\) và \(\left( {\frac{x}{y} + \frac{y}{x}} \right) + \left( {\frac{y}{z} + \frac{z}{y}} \right) + \left( {\frac{z}{x} + \frac{x}{z}} \right) =  - 2\).

Tính giá trị của biểu thức \(P = {x^{2025}} + {y^{2025}} + {z^{2025}}\).

--- HẾT ---

Lời giải chi tiết

Bài 1. (2 điểm) Giải các hệ phương trình sau:

a) \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}2x + y = 2\\3x - y =  - 7\end{array}\end{array}} \right.\)

b) \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\frac{1}{{x - y}} + \frac{4}{y} =  - \frac{{17}}{{15}}\\\frac{5}{{x - y}} - \frac{6}{y} = 3\end{array}\end{array}} \right.\) với \(x \ne y;y \ne 0\).

Phương pháp:

a) Sử dụng phương pháp cộng đại số để tìm nghiệm.

b) Đặt \(\frac{1}{{x - y}} = a;\frac{1}{y} = b\). Đưa hệ phương trình về hệ hai phương trình bậc nhất hai ẩn a, b để giải.

Sau khi giải hệ, thay lại để tìm x, y.

Lời giải:

a) \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}2x + y = 2\\3x - y =  - 7\end{array}\end{array}} \right.\)

\(\begin{array}{l}\left\{ \begin{array}{l}5x =  - 5\\3x - y =  - 7\end{array} \right.\\\left\{ \begin{array}{l}x =  - 1\\y = 3x + 7\end{array} \right.\\\left\{ \begin{array}{l}x =  - 1\\y = 3.\left( { - 1} \right) + 7\end{array} \right.\\\left\{ \begin{array}{l}x =  - 1\\y = 4\end{array} \right.\end{array}\)

Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( { - 1;4} \right)\).

b) \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\frac{1}{{x - y}} + \frac{4}{y} =  - \frac{{17}}{{15}}\\\frac{5}{{x - y}} - \frac{6}{y} = 3\end{array}\end{array}} \right.\) với \(x \ne y;y \ne 0\)

Đặt \(\frac{1}{{x - y}} = a;\frac{1}{y} = b\), hệ phương trình trở thành \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a + 4b =  - \frac{{17}}{{15}}\\5a - 6b = 3\end{array}\end{array}} \right.\)

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a =  - \frac{{17}}{{15}} - 4b\\5\left( { - \frac{{17}}{{15}} - 4b} \right) - 6b = 3\end{array}\end{array}} \right.\\\left\{ \begin{array}{l}a =  - \frac{{17}}{{15}} - 4b\\\frac{{ - 17}}{3} - 20b - 6b = 3\end{array} \right.\\\left\{ \begin{array}{l}a =  - \frac{{17}}{{15}} - 4b\\ - 26b = \frac{{26}}{3}\end{array} \right.\\\left\{ \begin{array}{l}a =  - \frac{{17}}{{15}} - 4b\\b =  - \frac{1}{3}\end{array} \right.\\\left\{ \begin{array}{l}a = \frac{1}{5}\\b =  - \frac{1}{3}\end{array} \right.\end{array}\)

Thay vào \(\frac{1}{{x - y}} = a;\frac{1}{y} = b\), ta được:

\(\frac{1}{{x - y}} = \frac{1}{5}\) suy ra \(x - y = 5\).

\(\frac{1}{y} =  - \frac{1}{3}\) suy ra \(y =  - 3\).

Do đó \(x = 5 + y = 5 + \left( { - 3} \right) = 2\).

Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {2; - 3} \right)\).

Bài 2. (2 điểm)

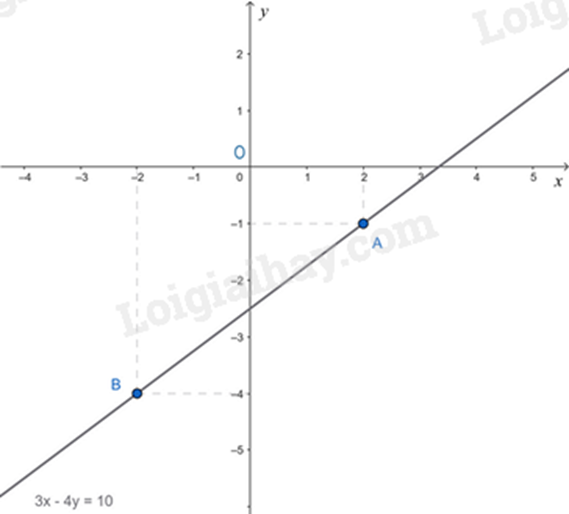
1) Cho phương trình: \(3x - 4y = m - 1\) (\(m\) là tham số).

a) Tìm \(m\) để cặp số \((2; - 1)\) là một nghiệm của phương trình.

b) Với \(m\) tìm được ở câu a, hãy biểu diễn tập nghiệm của phương trình trên mặt phẳng tọa độ \(Oxy\).

2) Cô Nguyệt có hai khoản đầu tư với lãi suất là 6% và 8% mỗi năm. Cô thu được tiền lãi từ hai khoản đầu tư đó là 150 triệu đồng mỗi năm. Nếu coi \(x\) (triệu đồng) là khoản đầu tư với lãi suất 6% và \(y\) (triệu đồng) là khoản đầu tư với lãi suất 8%, với \(x > 0;y > 0\). Hãy viết phương trình bậc nhất hai ẩn cho hai khoản đầu tư của cô Nguyệt.

3) Cho tam giác ABC có \(\hat A = 30^\circ \), \(AB = 3\) cm, \(AC = 4\) cm. Tính diện tích của tam giác ABC.

Phương pháp:

1) Thay nghiệm vào phương trình để tìm m.

b) Biểu diễn phương trình về hàm số \(y = ax + b\) \(\left( {a \ne 0} \right)\) để vẽ đồ thị.

- Lấy hai điểm bất kì thuộc đồ thị hàm số (nên chọn điểm có toạ độ nguyên để dễ vẽ hơn).

- Vẽ đường thẳng đi qua hai điểm đó, ta được đồ thị hàm số chính là tập nghiệm của phương trình.

2) Biểu diễn số tiền lãi thu được theo x, y rồi viết phương trình tổng tiền lãi từ hai khoản đầu tư đó là 150 triệu đồng.

3) Kẻ đường cao BH của tam giác ABC (\(H \in AC\)).

Áp dụng hệ thức lượng vào tam giác ABH vuông tại H để tính BH.

Áp dụng công thức tính diện tích tam giác: \(S = \frac{1}{2}\).chiều cao.đáy tương ứng.

Lời giải:

1) Thay \(\left( {x;y} \right) = (2; - 1)\) vào phương trình, ta được:

\(\begin{array}{l}3.2 - 4.\left( { - 1} \right) = m - 1\\6 + 4 = m - 1\\m = 10 + 1 = 11\end{array}\)

Vậy m = 11 thì cặp số \((2; - 1)\) là một nghiệm của phương trình.

b) Với m = 11, phương trình trở thành:

\(\begin{array}{l}3x - 4y = 11 - 1\\3x - 4y = 10\\4y = 3x - 10\\y = \frac{3}{4}x - \frac{5}{2}\end{array}\)

Tập nghiệm của phương trình được biểu diễn bởi đường thẳng \(y = \frac{3}{4}x - \frac{5}{2}\).

Cho \(x = 2\) thì \(y = \frac{3}{4}.2 - \frac{5}{2} =  - 1\), ta được điểm \(A\left( {2; - 1} \right)\).

Cho \(x =  - 2\) thì \(y = \frac{3}{4}.\left( { - 2} \right) - \frac{5}{2} =  - 4\), ta được điểm \(B\left( { - 2; - 4} \right)\).

Đường thẳng AB chính là tập nghiệm của phương trình \(3x - 4y = 10\).

2) Tiền lãi từ khoản đầu tư với lãi suất 6% là: \(\frac{6}{{100}}x = 0,06x\) (triệu đồng)

Tiền lãi từ khoản đầu tư với lãi suất 8% là: \(\frac{8}{{100}}y = 0,08y\) (triệu đồng)

Vì tổng tiền lãi thu được từ hai khoản đầu tư đó là 150 triệu đồng nên ta có phương trình: \(0,06x + 0,08y = 150\).

3)

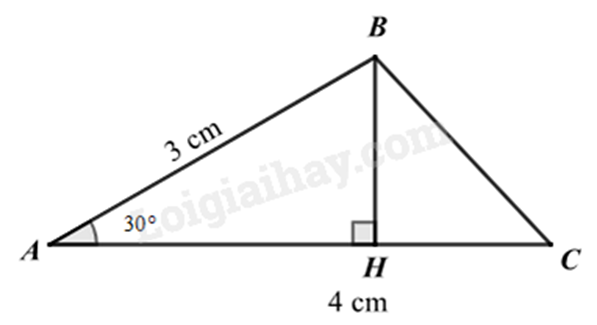
Kẻ đường cao BH của tam giác ABC (\(H \in AC\)).

Áp dụng hệ thức lượng vào tam giác ABH vuông tại H, ta có:

\(BH = AB.\sin A = 3.\sin 30^\circ  = 1,5\left( {cm} \right)\)

Diện tích tam giác ABC là:

\(S = \frac{1}{2}.BH.AC = \frac{1}{2}.1,5.4 = 3\left( {c{m^2}} \right)\)

Bài 3. (2 điểm) Bạn Dũng đi xe đạp từ địa điểm \(A\) đến địa điểm \(B\), bạn Trang cũng đi xe đạp, nhưng từ địa điểm \(B\) đến địa điểm \(A\). Hai bạn gặp nhau khi bạn Dũng đã đi được \(1\) giờ 30 phút, còn bạn Trang đã đi được \(2\) giờ. Một lần khác hai bạn cũng đi từ hai địa điểm như thế và trên cùng tuyến đường nhưng khởi hành đồng thời, sau \(1\) giờ 15 phút thì còn cách nhau 10,5 km. Tính vận tốc của mỗi bạn, biết rằng đoạn đường AB dài 38 km.

Phương pháp:

Gọi vận tốc của bạn Dũng và bạn Trang lần lượt là \(x,y\) (km/h), \(x,y > 0\).

Vì khi bạn Dũng đi 1 giờ 30 phút và bạn Trang đi 2 giờ thì gặp nhau nên hai bạn đã đi hết quãng đường AB nên ta viết được phương trình tổng quãng đường hai bạn đi bằng 38km.

Vì khi hai bạn đi được \(1\) giờ 15 phút thì còn cách nhau 10,5 km nên tổng quãng đường hai bạn đi + 10,5 km = 38 km nên ta có phương trình thứ hai.

Từ đó lập được hệ phương trình.

Giải hệ phương trình, kiểm tra điều kiện và kết luận.

Lời giải:

Gọi vận tốc của bạn Dũng và bạn Trang lần lượt là \(x,y\) (km/h), \(x,y > 0\).

Trong 1 giờ 30 phút = 1,5h bạn Dũng đi được \(1,5x\) (km).

Trong 2 giờ bạn Trang đi được đi được \(2y\) (km).

Vì hai bạn gặp nhau khi bạn Dũng đã đi được \(1\) giờ 30 phút, còn bạn Trang đã đi được \(2\) giờ nên ta có phương trình: \(1,5x + 2y = 38\) (1)

Trong 1 giờ 15 phút = 1,25h bạn Dũng đi được \(1,25x\) (km), bạn Trang đi được \(1,25y\) (km) và hai bạn cách nhau 10,5 km nên ta có phương trình: \(1,25x + 1,25y + 10,5 = 38\) hay \(1,25x + 1,25y = 27,5\) (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}1,5x + 2y = 38\\1,25x + 1,25y = 27,5\end{array} \right.\)

Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}x = 12\\y = 10\end{array} \right.\) (TM)

Vậy vận tốc của bạn Dũng là 12km/h, vận tốc của bạn Trang là 10km/h.

Bài 4. (3,5 điểm)

1) Bóng trên mặt đất của một cây dài 22 m. Tính chiều cao của cây (làm tròn kết quả đến hàng đơn vị), biết rằng tia nắng mặt trời tạo với mặt đất một góc \(35^\circ \).

2) Cho tam giác nhọn ABC\((\)AB < AC) có các đường cao BD, CE cắt nhau tại \(H\) (\(D \in AC\), \(E \in AB\)).

a) Chứng minh \(AE \cdot BD = AD \cdot CE\).

b) Qua \(B\) kẻ đường thẳng vuông góc với AB tại \(B\) và qua \(C\) kẻ đường thẳng vuông góc với AC tại \(C\), hai đường thẳng này cắt nhau tại \(K\). Chứng minh tứ giác BHCK là hình bình hành và \(\widehat {BAH} = \widehat {CAK}\).

c) Gọi \(O\) là giao điểm của BC và HK. Đoạn thẳng AH cắt ED tại \(M\) và đoạn thẳng AK cắt BC tại \(N\). Chứng minh AO đi qua trung điểm \(I\) của đoạn thẳng MN.

Phương pháp:

1) Áp dụng hệ thức lượng trong tam giác để tính chiều cao của cây.

2)

a) Chứng minh $\Delta ABD\backsim \Delta ACE$ (g.g), suy ra \(AE \cdot BD = AD \cdot CE\).

b) * BHCK là hình bình hành

Chứng minh tứ giác BHCK có hai cặp cạnh đối song song nên là hình bình hành.

* Chứng minh \(\widehat {BAH} = \widehat {CAK}\)

Chứng minh \(\frac{{EH}}{{CK}} = \frac{{EA}}{{AC}}\) và \(\widehat {AEH} = \widehat {ACK}\left( { = 90^\circ } \right)\) suy ra $\Delta AEH\backsim \Delta ACK$ (c.g.c).

Do đó \(\widehat {BAH} = \widehat {KAC}\).

c) Chứng minh HO = OK.

Chứng minh \(\frac{{AH}}{{AK}} = \frac{{AE}}{{AC}}\)

Chứng minh $\Delta ADE\backsim \Delta ABC$ (c.g.c) suy ra \(\widehat {AED} = \widehat {ACB}\)

Kết hợp điều kiện để chứng minh $\Delta AEM\backsim ACN$ (g.g), suy ra \(\frac{{AE}}{{AC}} = \frac{{AM}}{{AN}}\)

Chứng minh được MN // HK (định lí Thalès đảo).

Sử dụng định lí tam giác đồng dạng hoặc hệ quả của định lí Thalès để chứng minh \(\frac{{MI}}{{HO}} = \frac{{AI}}{{AO}}\), \(\frac{{IN}}{{OK}} = \frac{{AI}}{{AO}}\). Suy ra \(\frac{{MI}}{{HO}} = \frac{{IN}}{{OK}}\).

Do đó I là trung điểm của HN. Ta được điều phải chứng minh

Lời giải:

1) Chiều cao của cây là:

\(22.\tan 35^\circ  \approx 15\left( m \right)\).

2)

a)

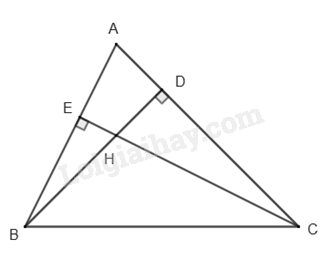
Xét \(\Delta ABD\) và \(\Delta ACE\) có:

\(\widehat A\) chung

\(\widehat D = \widehat E\left( { = 90^\circ } \right)\)

nên $\Delta ABD\backsim \Delta ACE$ (g.g), suy ra \(\frac{{BD}}{{CE}} = \frac{{AD}}{{AE}}\)

Do đó \(AE \cdot BD = AD \cdot CE\).

b)

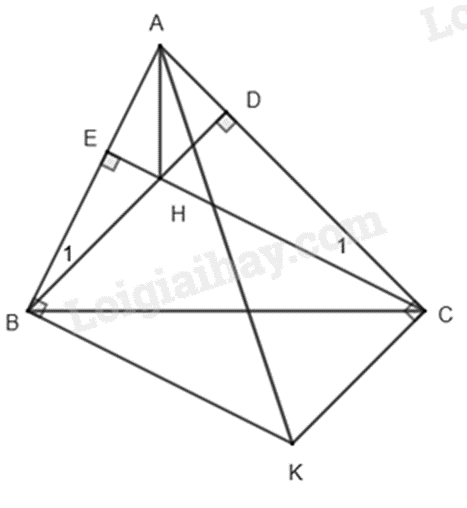
* BHCK là hình bình hành

Vì \(BD \bot AC\) và \(CK \bot AC\) nên \(BD//CK\).

Vì \(CE \bot AB\) và \(BK \bot AB\) nên \(CE//BK\).

Xét tứ giác BHCK có:

CK // BH (do CE // BK)

BK // CH (do BD // CK)

nên tứ giác BHCK là hình bình hành.

* Chứng minh \(\widehat {BAH} = \widehat {CAK}\)

Vì $\Delta ABD\backsim \Delta ACE$ (câu a) nên \(\widehat {{B_1}} = \widehat {{C_1}}\) (hai góc tương ứng)

Xét \(\Delta BEH\) và \(\Delta CEA\) có:

\(\widehat {{B_1}} = \widehat {{C_1}}\) (cmt)

\(\widehat {BEH} = \widehat {CEA}\left( { = 90^\circ } \right)\)

Do đó $\Delta BEH\backsim \Delta CEA$ (g.g)

Suy ra \(\frac{{EH}}{{BH}} = \frac{{EA}}{{AC}}\)

Mà BH = CK (do BHCK là hình bình hành) nên \(\frac{{EH}}{{CK}} = \frac{{EA}}{{AC}}\)

Kết hợp với \(\widehat {AEH} = \widehat {ACK}\left( { = 90^\circ } \right)\)

Suy ra $\Delta AEH\backsim \Delta ACK$ (c.g.c).

Do đó \(\widehat {EAH} = \widehat {CAK}\) hay \(\widehat {BAH} = \widehat {KAC}\).

c)

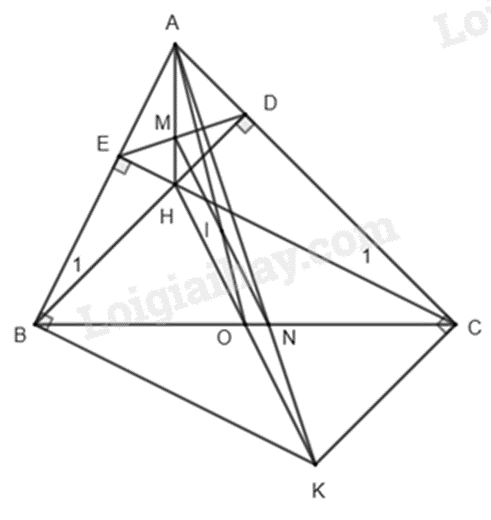
Vì O là giao điểm của hai đường chéo HK và BC của hình bình hành BHCK nên O là trung điểm của HK, do đó HO = OK.

Vì $\Delta AEH\backsim \Delta ACK$ (câu b) nên \(\frac{{AH}}{{AK}} = \frac{{AE}}{{AC}}\) (1)

Vì $\Delta ABD\backsim \Delta ACE$ nên \(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\). .Kết hợp với \(\widehat A\) chung suy ra $\Delta ADE\backsim \Delta ABC$ (c.g.c)

Suy ra \(\widehat {AED} = \widehat {ACB}\)

Xét \(\Delta AEM\) và \(\Delta ACN\) có:

\(\widehat {EAM} = \widehat {CAN}\) (cmt)

\(\widehat {AEM} = \widehat {ACN}\) (cmt)

Do đó $\Delta AEM\backsim ACN$ (g.g), suy ra \(\frac{{AE}}{{AC}} = \frac{{AM}}{{AN}}\) (2)

Từ (1) và (2) suy ra \(\frac{{AH}}{{AK}} = \frac{{AM}}{{AN}}\) hay \(\frac{{AM}}{{AH}} = \frac{{AN}}{{AK}}\). Do đó MN // HK (định lí Thalès đảo).

Ta có I là giao điểm của AO và MN.

Vì MI // HO nên $\Delta AMI\backsim \Delta AHO$ (định lí tam giác đồng dạng), suy ra $\frac{MI}{HO}=\frac{AI}{AO}$ (3).

Vì IN // OK nên $\Delta AIN\backsim \Delta AOK$ (định lí tam giác đồng dạng), suy ra \(\frac{{IN}}{{OK}} = \frac{{AI}}{{AO}}\) (4).

Từ (3) và (4) suy ra \(\frac{{MI}}{{HO}} = \frac{{IN}}{{OK}}\).

Mà OH = OK (cmt) nên MI = IN hay I là trung điểm của HN.

Vậy AO đi qua trung điểm \(I\) của đoạn thẳng MN.

Bài 5. (0,5 điểm) Cho các số x, y, z khác \(0\) thỏa mãn: \(x + y + z = 1\) và \(\left( {\frac{x}{y} + \frac{y}{x}} \right) + \left( {\frac{y}{z} + \frac{z}{y}} \right) + \left( {\frac{z}{x} + \frac{x}{z}} \right) =  - 2\).

Tính giá trị của biểu thức \(P = {x^{2025}} + {y^{2025}} + {z^{2025}}\).

Phương pháp:

Biến đổi phương trình \(\left( {\frac{x}{y} + \frac{y}{x}} \right) + \left( {\frac{y}{z} + \frac{z}{y}} \right) + \left( {\frac{z}{x} + \frac{x}{z}} \right) =  - 2\) về dạng \(A.B.C = 0\), ta có 3 trường hợp:

\(A = 0;B = 0\) và \(C = 0\).

Lời giải:

Ta có:

\(\begin{array}{l}\left( {\frac{x}{y} + \frac{y}{x}} \right) + \left( {\frac{y}{z} + \frac{z}{y}} \right) + \left( {\frac{z}{x} + \frac{x}{z}} \right) =  - 2\\\frac{{{x^2} + {y^2}}}{{xy}} + \frac{{{y^2} + {z^2}}}{{yz}} + \frac{{{z^2} + {x^2}}}{{xz}} =  - 2\\\frac{{{x^2}z + {y^2}z}}{{xyz}} + \frac{{x{y^2} + x{z^2}}}{{xyz}} + \frac{{y{z^2} + {x^2}y}}{{xyz}} =  - 2\\{x^2}z + {y^2}z + x{y^2} + x{z^2} + y{z^2} + {x^2}y =  - 2xyz\\{x^2}z + {y^2}z + x{y^2} + x{z^2} + y{z^2} + {x^2}y + 2xyz = 0\\\left( {x{y^2} + 2xyz + x{z^2}} \right) + {x^2}z + {y^2}z + y{z^2} + {x^2}y = 0\\x\left( {{y^2} + 2yz + {z^2}} \right) + \left( {{x^2}y + {x^2}z} \right) + \left( {{y^2}z + y{z^2}} \right) = 0\\x{\left( {y + z} \right)^2} + {x^2}\left( {y + z} \right) + yz\left( {y + z} \right) = 0\\\left( {y + z} \right)\left[ {x\left( {y + z} \right) + {x^2} + yz} \right] = 0\\\left( {y + z} \right)\left[ {xy + xz + {x^2} + yz} \right] = 0\\\left( {y + z} \right)\left[ {\left( {{x^2} + xy} \right) + xz + yz} \right] = 0\\\left( {y + z} \right)\left[ {x\left( {x + y} \right) + z\left( {x + y} \right)} \right] = 0\\\left( {y + z} \right)\left( {x + z} \right)\left( {x + y} \right) = 0\end{array}\)

Do đó \(y + z = 0\) hoặc \(x + z = 0\) hoặc \(x + y = 0\).

+) Với \(y + z = 0\) thì \(x + 0 = 1\) suy ra \(x = 1\), ta được \(\left( {x,y,z} \right) = \left( {1;0;0} \right)\).

+) Với \(x + z = 0\) thì \(y + 0 = 1\) suy ra \(y = 1\), ta được \(\left( {x,y,z} \right) = \left( {0;1;0} \right)\).

+) Với \(x + y = 0\) thì \(z + 0 = 1\) suy ra \(z = 1\), ta được \(\left( {x,y,z} \right) = \left( {0;0;1} \right)\).

Khi đó

\(\begin{array}{l}P = {1^{2025}} + {0^{2025}} + {0^{2025}}\\ = {0^{2025}} + {1^{2025}} + {0^{2025}}\\ = {0^{2025}} + {0^{2025}} + {1^{2025}}\\ = 1\end{array}\)

Vậy \(P = 1\).