 Đề thi toán 9, đề kiểm tra toán 9 kết nối tri thức có đáp án và lời giải chi tiết
Đề thi toán 9, đề kiểm tra toán 9 kết nối tri thức có đáp án và lời giải chi tiết
 Đề khảo sát chất lượng đầu năm Toán 9 - Kết nối tri thức
Đề khảo sát chất lượng đầu năm Toán 9 - Kết nối tri thức Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
Bài 1 (1,5 điểm). Cho hai biểu thức:
Đề bài
Bài 1 (1,5 điểm).
Cho hai biểu thức: \(A = \frac{{x + 2}}{{x - 3}}\) và \(B = \frac{{{x^2} - 2x + 4}}{{{x^2} + 2x}} + \frac{6}{{x + 2}}\) \(\left( {x \ne - 2;x \ne 0;x \ne 3} \right)\)
a) Tính giá trị của biểu thức \(A\) tại \(x = - 4\);
b) Chứng minh \(B = \frac{{x + 2}}{x}\);
c) Tìm các giá trị nguyên của \(x\) để biểu thức \(\frac{A}{B}\) nhận giá trị nguyên.
Bài 2 (2,0 điểm). Giải các bài toán sau bằng cách lập phương trình
1) Lúc 7 giờ sáng, một xe máy xuất phát từ bến xe Mỹ Đình – Hà Nội đến bến xe Sơn La – Sơn La. Sau đó 1 giờ, một ô tô cũng xuất phát từ bến xe Mỹ Đình – Hà Nội đến bến xe Sơn La – Sơn La trên cùng một tuyến đường với xe máy. Biết ô tô đi được 4 giờ thì đuổi kịp xe máy. Tính vận tốc của xe máy và vận tốc của ô tô. Biết vận tốc ô tô hơn vận tốc xe máy là \(10km/h\).
2) Để mở rộng kinh doanh, một cửa hàng đã vay 600 triệu đồng, kì hạn 12 tháng từ hai ngân hàng A và B với lãi suất lần lượt là 8%/năm và 9%/năm. Tổng số tiền lãi một năm phải trả cho cả hai ngân hàng là 50 triệu đồng. Tính số tiền cửa hàng đã vay từ mỗi ngân hàng.
Bài 3 (2,0 điểm). Giải các hệ phương trình sau:
a) \(\left\{ {\begin{array}{*{20}{l}}{2x - 3y = 7}\\{3x + 4y = 2}\end{array}} \right.\)
b) \(\left\{ {\begin{array}{*{20}{l}}{\frac{1}{{\left| x \right|}} + y = 2}\\{\frac{2}{{\left| x \right|}} + 3y = 5}\end{array}} \right.\)
Bài 4 (4,0 điểm).
1) Một con tàu đang gặp sự cố trên biển, chủ tàu phát hiện ra một ngọn hải đăng ở gần và dùng giác kế đo được góc giữa tia nắng chiếu từ đỉnh ngọn hải đăng với phương nằm ngang là \({10^ \circ }\). Biết ngọn hải đăng cao \(42m\) tính từ mặt nước biển (Hình vẽ).
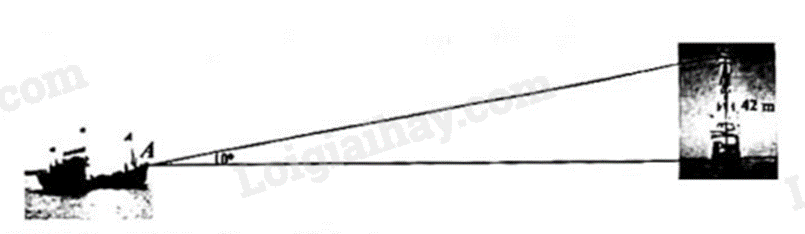
a) Tính khoảng cách từ tàu đến ngọn hải đăng;
b) Biết rằng tàu cứu hộ có vận tốc là \(10km/h\). Hỏi tàu cứu hộ mất bao nhiêu phút để đi từ ngọn hải đăng đến chỗ tàu gặp nạn.
(Làm tròn các kết quả đến chữ số thập phân thứ nhất).
2) Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\).
a) Chứng minh rằng \(A{B^2} = BH.BC\).
b) Giả sử \(AB = 3cm\), \(BC = 5cm\). Giải tam giác vuông \(ABH\) (kết quả số đo góc làm tròn đến phút).
c) Gọi \(M,N\) lần lượt là hình chiếu của \(H\) trên \(AB,AC\). Chứng minh \({\rm{\Delta }}AMN\) đồng dạng với \({\rm{\Delta }}ACB\) và \({S_{{\rm{\Delta }}ABC}} = \frac{{{S_{{\rm{\Delta }}MHN}}}}{{{\rm{co}}{{\rm{s}}^2}B{\rm{co}}{{\rm{s}}^2}C}}\).
Bài 5 (0,5 điểm).
Bác An cắt một sợi dây thép dài \(30cm\) thành hai đoạn. Mỗi đoạn được uốn thành một hình vuông. Bác An căng vải trên hai khung đó. Hỏi cần cắt đoạn dây như thế nào để tổng diện tích phần vải căng đạt giá trị nhỏ nhất (coi mép vải thừa không đáng kể).
---- Hết ----
Lời giải
Bài 1 (1,5 điểm).
Cho hai biểu thức: \(A = \frac{{x + 2}}{{x - 3}}\) và \(B = \frac{{{x^2} - 2x + 4}}{{{x^2} + 2x}} + \frac{6}{{x + 2}}\) \(\left( {x \ne - 2;x \ne 0;x \ne 3} \right)\)
a) Tính giá trị của biểu thức \(A\) tại \(x = - 4\);
b) Chứng minh \(B = \frac{{x + 2}}{x}\);
c) Tìm các giá trị nguyên của \(x\) để biểu thức \(\frac{A}{B}\) nhận giá trị nguyên.
Phương pháp:
a) Thay \(x = - 4\) (TMĐK) vào A để tính giá trị của A.
b) Thực hiện quy đồng mẫu để rút gọn B.
c) Tính \(\frac{A}{B}\).
Tách \(\frac{A}{B}\) thành dạng \(\frac{A}{B} = h\left( x \right) + \frac{m}{{g\left( x \right)}}\) trong đó h(x) là một biểu thức nguyên khi x nguyên, m nguyên.
Biện luận \(\frac{A}{B}\) nguyên khi \(\frac{m}{{g\left( x \right)}}\) nguyên, suy ra \(g\left( x \right) \in \)Ư(m).
Từ đó giải tìm x.
Lời giải:
a) Thay \(x = - 4\) (TMĐK) vào A, ta được:
\(A = \frac{{ - 4 + 2}}{{ - 4 - 3}} = \frac{{ - 2}}{{ - 7}} = \frac{2}{7}\)
Vậy \(A = \frac{2}{7}\) khi \(x = - 4\).
b) Ta có:
\(\begin{array}{l}B = \frac{{{x^2} - 2x + 4}}{{{x^2} + 2x}} + \frac{6}{{x + 2}}\\ = \frac{{{x^2} - 2x + 4}}{{x\left( {x + 2} \right)}} + \frac{{6x}}{{x\left( {x + 2} \right)}}\\ = \frac{{{x^2} + 4x + 4}}{{x\left( {x + 2} \right)}}\\ = \frac{{{{\left( {x + 2} \right)}^2}}}{{x\left( {x + 2} \right)}}\\ = \frac{{x + 2}}{x}\end{array}\)
Vậy \(B = \frac{{x + 2}}{x}\).
c) Ta có:
\(\frac{A}{B} = \frac{{x + 2}}{{x - 3}}:\frac{{x + 2}}{x} = \frac{{x + 2}}{{x - 3}}.\frac{x}{{x + 2}} = \frac{x}{{x - 3}} = \frac{{x - 3 + 3}}{{x - 3}} = 1 + \frac{3}{{x - 3}}\)
Để \(\frac{A}{B}\) nhận giá trị nguyên thì \(\frac{3}{{x - 3}}\) nguyên hay \(3 \vdots \left( {x - 3} \right)\), suy ra \(\left( {x - 3} \right) \in \)Ư(3) = \(\left\{ { - 3; - 1;1;3} \right\}\).
Ta có bảng giá trị sau:
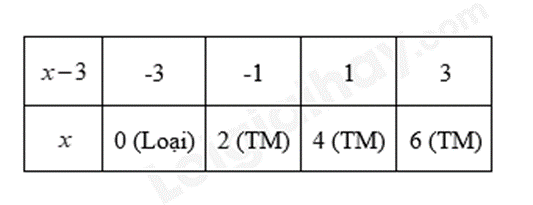
Vậy \(x \in \left\{ {2;4;6} \right\}\) thì biểu thức \(\frac{A}{B}\) nhận giá trị nguyên.
Bài 2 (2,0 điểm). Giải các bài toán sau bằng cách lập phương trình
1) Lúc 7 giờ sáng, một xe máy xuất phát từ bến xe Mỹ Đình – Hà Nội đến bến xe Sơn La – Sơn La. Sau đó 1 giờ, một ô tô cũng xuất phát từ bến xe Mỹ Đình – Hà Nội đến bến xe Sơn La – Sơn La trên cùng một tuyến đường với xe máy. Biết ô tô đi được 4 giờ thì đuổi kịp xe máy. Tính vận tốc của xe máy và vận tốc của ô tô. Biết vận tốc ô tô hơn vận tốc xe máy là \(10km/h\).
2) Để mở rộng kinh doanh, một cửa hàng đã vay 600 triệu đồng, kì hạn 12 tháng từ hai ngân hàng A và B với lãi suất lần lượt là 8%/năm và 9%/năm. Tổng số tiền lãi một năm phải trả cho cả hai ngân hàng là 50 triệu đồng. Tính số tiền cửa hàng đã vay từ mỗi ngân hàng.
Phương pháp:
1) Gọi vận tốc xe máy là \(x\left( {km/h} \right)\), \(x > 0\).
Biểu diễn vận tốc của ô tô theo \(x\).
Từ đó biểu diễn quãng đường xe máy, quãng đường ô tô đi được.
Vì ô tô và xe máy đi cùng một tuyến đường nên tại thời điểm ô tô đuổi kịp xe máy thì quãng đường ô tô và xe máy đi được là bằng nhau nên ta lập được phương trình.
Giải phương trình.
Kiểm tra điều kiện và kết luận.
2) Gọi số tiền cửa hàng vay từ ngân hàng A và B lần lượt là \(x\) và \(y\) (triệu đồng, \(0 < x,y < 600\))
Vì tổng số tiền cửa hàng đã vay là 600 triệu nên ta lập được phương trình thứ nhất.
Vì lãi suất của ngân hàng A và B lần lượt là 8%/năm và 9%/năm và tổng số tiền lãi một năm phải trả là 50 triệu đồng nên ta lập được phương trình thứ hai.
Từ đó ta có hệ phương trình.
Giải hệ phương trình.
Kiểm tra điều kiện và kết luận.
Lời giải:
1) Gọi vận tốc xe máy là \(x\left( {km/h} \right)\), \(x > 0\).
Vì vận tốc ô tô hơn vận tốc xe máy là 10km/h nên vận tốc của ô tô là: \(x + 10\left( {km/h} \right)\).
Vì xe máy đi trước ô tô 1 giờ nên tổng thời gian xe máy đi đến khi ô tô đuổi kịp xe máy là 1 + 4 = 5 (giờ), khi đó quãng đường xe máy đi được là \(5x\left( {km} \right)\).
Vì ô tô đi được 4 giờ thì đuổi kịp xe máy nên quãng đường ô tô đi là: \(4\left( {x + 10} \right)\) \(\left( {km} \right)\).
Vì ô tô và xe máy đi cùng một tuyến đường nên tại thời điểm ô tô đuổi kịp xe máy thì quãng đường ô tô và xe máy đi được là bằng nhau nên ta có phương trình:
\(\begin{array}{l}5x = 4\left( {x + 10} \right)\\5x - 4x = 40\\x = 40\left( {TM} \right)\end{array}\)
Suy ra vận tốc ô tô là: 40 + 10 = 50(km/h)
Vậy vận tốc của xe máy là 40km/h, vận tốc của ô tô là 50km/h.
2) Gọi số tiền cửa hàng vay từ ngân hàng A và B lần lượt là \(x\) và \(y\) (triệu đồng, \(0 < x,y < 600\))
Vì tổng số tiền cửa hàng đã vay là 600 triệu đồng nên ta có phương trình \(x + y = 600\) (1)
Vì lãi suất của ngân hàng A và B lần lượt là 8%/năm và 9%/năm và tổng số tiền lãi một năm phải trả là 50 triệu đồng nên ta có phương trình:
\(8\% x + 9\% y = 50\) hay \(0,08x + 0,09y = 50\) (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 600\\0,08x + 0,09y = 50\end{array} \right.\)
Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}x = 400\\y = 200\end{array} \right.\left( {TM} \right)\)
Vậy số tiền cửa hàng đã vay từ ngân hàng A và B lần lượt là 400 triệu và 200 triệu.
Bài 3 (2,0 điểm). Giải các hệ phương trình sau:
a) \(\left\{ {\begin{array}{*{20}{l}}{2x - 3y = 7}\\{3x + 4y = 2}\end{array}} \right.\) b) \(\left\{ {\begin{array}{*{20}{l}}{\frac{1}{{\left| x \right|}} + y = 2}\\{\frac{2}{{\left| x \right|}} + 3y = 5}\end{array}} \right.\)
Phương pháp:
a) Giải hệ phương trình bằng phương pháp cộng đại số.
b) Đặt ẩn phụ \(\frac{1}{{\left| x \right|}} = t\), đưa hệ phương trình về hệ hai phương trình bậc nhất ẩn t, y.
Giải hệ phương trình bằng phương pháp thế để tìm t, y.
Thay lại t vào \(\frac{1}{{\left| x \right|}} = t\) để tính \(x\).
Lời giải:
a) \(\left\{ {\begin{array}{*{20}{l}}{2x - 3y = 7}\\{3x + 4y = 2}\end{array}} \right.\)
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{8x - 12y = 28}\\{9x + 12y = 6}\end{array}} \right.\\\left\{ \begin{array}{l}17x = 34\\3x + 4y = 2\end{array} \right.\\\left\{ \begin{array}{l}x = 2\\y = \frac{{2 - 3x}}{4}\end{array} \right.\\\left\{ \begin{array}{l}x = 2\\y = - 1\end{array} \right.\end{array}\)
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {2; - 1} \right)\).
b) \(\left\{ {\begin{array}{*{20}{l}}{\frac{1}{{\left| x \right|}} + y = 2}\\{\frac{2}{{\left| x \right|}} + 3y = 5}\end{array}} \right.\)
Đặt \(\frac{1}{{\left| x \right|}} = t\), hệ phương trình trở thành: \(\left\{ \begin{array}{l}t + y = 2\\2t + 3y = 5\end{array} \right.\).
Giải hệ phương trình:
\(\begin{array}{l}\left\{ \begin{array}{l}t = 2 - y\\2\left( {2 - y} \right) + 3y = 5\end{array} \right.\\\left\{ \begin{array}{l}t = 2 - y\\4 - 2y + 3y = 5\end{array} \right.\\\left\{ \begin{array}{l}t = 2 - y\\y = 1\end{array} \right.\\\left\{ \begin{array}{l}t = 1\\y = 1\end{array} \right.\end{array}\)
Thay t, ta được \(\frac{1}{{\left| x \right|}} = 1\), suy ra \(\left| x \right| = 1\) nên \(x = \pm 1\).
Vậy nghiệm của hệ phương trình là \(\left( {x,y} \right) \in \left\{ {\left( {1;1} \right),\left( { - 1;1} \right)} \right\}\)
Bài 4 (4,0 điểm).
1) Một con tàu đang gặp sự cố trên biển, chủ tàu phát hiện ra một ngọn hải đăng ở gần và dùng giác kế đo được góc giữa tia nắng chiếu từ đỉnh ngọn hải đăng với phương nằm ngang là ${{10}^{\circ }}$. Biết ngọn hải đăng cao $42m$ tính từ mặt nước biển (Hình vẽ).
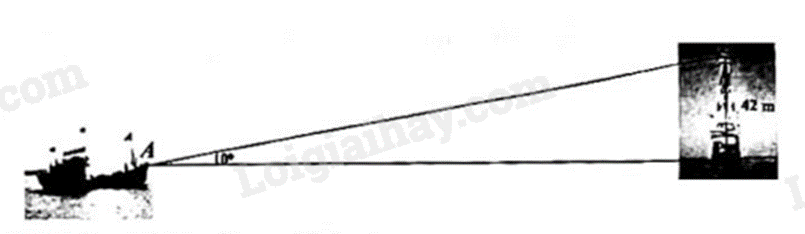
a) Tính khoảng cách từ tàu đến ngọn hải đăng;
b) Biết rằng tàu cứu hộ có vận tốc là $10km/h$. Hỏi tàu cứu hộ mất bao nhiêu phút để đi từ ngọn hải đăng đến chỗ tàu gặp nạn.
(Làm tròn các kết quả đến chữ số thập phân thứ nhất).
2) Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH$.
a) Chứng minh rằng $A{{B}^{2}}=BH.BC$.
b) Giả sử $AB=3cm$, $BC=5cm$. Giải tam giác vuông $ABH$ (kết quả số đo góc làm tròn đến phút).
c) Gọi $M,N$ lần lượt là hình chiếu của $H$ trên $AB,AC$. Chứng minh $\text{ }\!\!\Delta\!\!\text{ }AMN$ đồng dạng với $\text{ }\!\!\Delta\!\!\text{ }ACB$ và ${{S}_{\text{ }\!\!\Delta\!\!\text{ }ABC}}=\frac{{{S}_{\text{ }\!\!\Delta\!\!\text{ }MHN}}}{\text{co}{{\text{s}}^{2}}B\text{co}{{\text{s}}^{2}}C}$.
Phương pháp:
1)
a) Xác định tỉ số lượng giác tương ứng liên quan đến $10{}^\circ $ và 42m để tính khoảng cách từ tàu đến ngọn hải đăng là đoạn thẳng AB.
b) Xác định thời gian đi = quãng đường : vận tốc.
Lưu ý đổi về cùng đơn vị.
2)
a) Chứng minh rằng $A{{B}^{2}}=BH.BC$.
Chứng minh $\Delta ABC\backsim \Delta HBA\left( g.g \right)$, suy ra $A{{B}^{2}}=BH.BC$.
b) Giải tam giác vuông $ABH$ (kết quả số đo góc làm tròn đến phút).
Từ $A{{B}^{2}}=BH.BC$ (cmt), tính $BH$.
Áp dụng định lí Pythagore vào tam giác ABH để tính AH.
Áp dụng tỉ số lượng giác trong tam giác ABH, tính góc B.
Từ đó suy ra số đo góc BAH.
$\sin B=\frac{AH}{AB}=\frac{12}{5}:3=\frac{4}{5}$ nên $B\approx 53{}^\circ 8'$.
c) * Chứng minh $\Delta AMN\backsim \Delta ACB$
Gọi I là giao điểm của MN và AH.
Chứng minh tứ giác AMHN là hình chữ nhật suy ra MN và AH cắt nhau tại trung điểm của mỗi đường, nên $\Delta MIA$ cân tại I, suy ra hai góc ở đáy bằng nhau.
Từ đó chứng minh $\Delta AMN\backsim \Delta ACB$ (g.g)
* Chứng minh ${{S}_{\text{ }\!\!\Delta\!\!\text{ }ABC}}=\frac{{{S}_{\text{ }\!\!\Delta\!\!\text{ }MHN}}}{\text{co}{{\text{s}}^{2}}B\text{co}{{\text{s}}^{2}}C}$
Dựa vào đặc điểm của hình chữ nhật và tính chất hai đường thẳng song song suy ra các cặp góc đồng vị bằng nhau,
Chứng minh $\Delta AMN=\Delta HNM$, dẫn đến $\Delta HMN\backsim \Delta ABC$.
Suy ra \(\frac{{{S}_{\Delta HMN}}}{{{S}_{\Delta ABC}}}=\frac{HM.HN}{AB.AC}\)
Nhân cả tử và mẫu với BH.HC, từ đó biến đổi về tỉ số lượng giác cosin của góc B, C để chứng minh \(\frac{{{S}_{\Delta HMN}}}{{{S}_{\Delta ABC}}}={{\cos }^{2}}B.{{\cos }^{2}}C\)
Do đó ${{S}_{\Delta ABC}}=\frac{{{S}_{\Delta MHN}}}{{{\cos }^{2}}B.{{\cos }^{2}}C}$.
Lời giải:
1)
a)
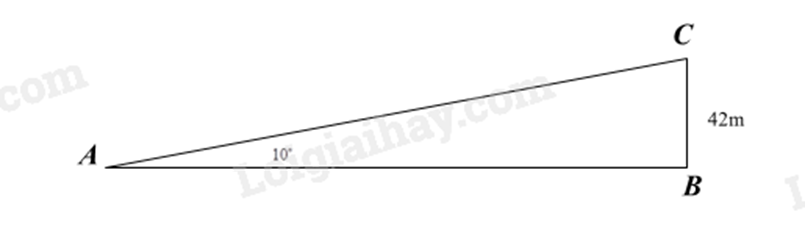
Gọi các điểm như hình vẽ.
Khi đó $\widehat{BAC}=10{}^\circ ,BC=42m$. Khoảng cách từ tàu đến ngọn hải đăng là đoạn thẳng AB.
Áp dụng tỉ số lượng giác vào tam giác ABC vuông tại B, ta có:
$\tan CAB=\frac{BC}{AB}$ suy ra $AB=\frac{BC}{\tan CAB}=\frac{42}{\tan 10{}^\circ }\approx 238,2\left( m \right)$
Vậy khoảng cách từ tàu đến ngọn hải đăng khoảng 238,2m.
b) Vì khoảng cách từ ngọn hải đăng đến chỗ tàu gặp nạn khoảng 238,2m = 0,2382km nên thời gian để tàu cứu hộ đi từ ngọn hải đăng đến chỗ tàu gặp nạn là:
0,2382 : 10 = 0,2382 (h) = 1,4292 (h) $\approx 1,4$ (phút).
2)
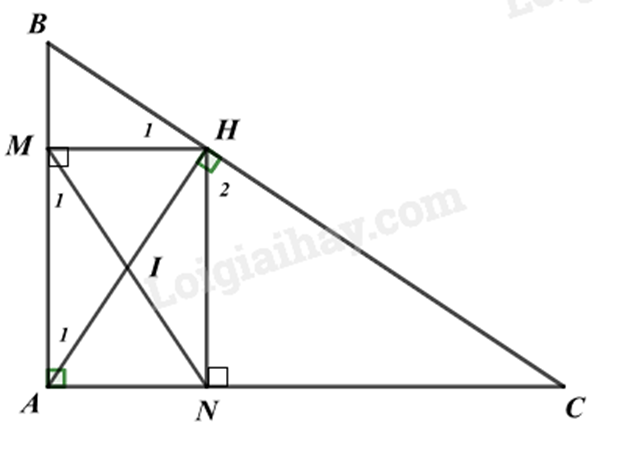
a) Chứng minh rằng $A{{B}^{2}}=BH.BC$.
Xét $\Delta ABC$ và $\Delta HBA$ có:
$\widehat{BAC}=\widehat{BHA}$ $\left( =90{}^\circ \right)$
$\widehat{B}$ chung
Do đó $\Delta ABC\backsim \Delta HBA\left( g.g \right)$, suy ra $\frac{AB}{BC}=\frac{BH}{AB}$ nên $A{{B}^{2}}=BH.BC$.
b) Giả sử $AB=3cm$, $BC=5cm$. Giải tam giác vuông $ABH$ (kết quả số đo góc làm tròn đến phút).
Vì $A{{B}^{2}}=BH.BC$ (cmt) nên $BH=\frac{A{{B}^{2}}}{BC}=\frac{{{3}^{2}}}{5}=\frac{9}{5}\left( cm \right)$.
Áp dụng định lí Pythagore vào tam giác ABH, ta có:
$A{{H}^{2}}=A{{B}^{2}}-B{{H}^{2}}={{3}^{2}}-{{\left( \frac{9}{5} \right)}^{2}}=\frac{144}{25}$, suy ra $AH=\sqrt{\frac{144}{25}}=\frac{12}{5}\left( cm \right)$.
Áp dụng tỉ số lượng giác trong tam giác ABH, ta có:
$\sin B=\frac{AH}{AB}=\frac{12}{5}:3=\frac{4}{5}$ nên $B\approx 53{}^\circ 8'$.
Suy ra $\widehat{BAH}=90{}^\circ -53{}^\circ 8'=36{}^\circ 52'$.
Vậy $AH=\frac{12}{5}cm,BH=\frac{9}{5}cm,AB=3cm$, $\widehat{AHB}=90{}^\circ ,\widehat{ABH}=53{}^\circ 8',\widehat{BAH}=36{}^\circ 52'$,
c) Gọi \(M,N\) lần lượt là hình chiếu của \(H\) trên \(AB,AC\). Chứng minh \({\rm{\Delta }}AMN\) đồng dạng với \({\rm{\Delta }}ACB\) và \({S_{{\rm{\Delta }}ABC}} = \frac{{{S_{{\rm{\Delta }}MHN}}}}{{{\rm{co}}{{\rm{s}}^2}B{\rm{co}}{{\rm{s}}^2}C}}\).
* Chứng minh $\Delta AMN\backsim \Delta ACB$
Gọi I là giao điểm của MN và AH.
Xét tứ giác AMHN có:
$\widehat{MAN}=90{}^\circ $ (gt)
$\widehat{AMH}=\widehat{ANH}$ (do $M,N$ lần lượt là hình chiếu của $H$ trên $AB,AC$)
nên tứ giác AMHN là hình chữ nhật.
Suy ra MN và AH cắt nhau tại trung điểm của mỗi đường, do đó MI = IH = IN = IA, suy ra $\Delta MIA$ cân tại I, suy ra $\widehat{{{M}_{1}}}=\widehat{{{A}_{1}}}$ (tính chất tam giác cân).
Mà $\widehat{{{A}_{1}}}+\widehat{B}=90{}^\circ $, $\widehat{B}+\widehat{C}=90{}^\circ $ nên $\widehat{{{A}_{1}}}=\widehat{C}$, suy ra $\widehat{{{M}_{1}}}=\widehat{C}$
Xét $\Delta AMN$ và $\Delta ACB$ có:
$\widehat{BAC}$ chung
$\widehat{{{M}_{1}}}=\widehat{C}$
Do đó $\Delta AMN\backsim \Delta ACB$ (g.g)
* Chứng minh \({S_{\Delta ABC}} = \frac{{{S_{\Delta MHN}}}}{{{\rm{co}}{{\rm{s}}^2}B{\rm{co}}{{\rm{s}}^2}C}}\)
Vì AMHN là hình chữ nhật nên MH // AC và NH // AB, suy ra $\widehat{{{H}_{1}}}=\widehat{C},\widehat{{{H}_{2}}}=\widehat{B}$
Xét $\Delta AMN$ và $\Delta HNM$ có:
\(AM=HN\) (vì AMHN là hình chữ nhật)
\(\widehat{MAB}=\widehat{NHM}\left( =90{}^\circ \right)\)
$AN=HM$ (vì AMHN là hình chữ nhật)
nên $\Delta AMN=\Delta HNM$.
Mà $\Delta AMN\backsim \Delta ACB$, suy ra $\Delta HMN\backsim \Delta ABC$.
Suy ra \(\frac{{{S}_{\Delta HMN}}}{{{S}_{\Delta ABC}}}=\frac{HM.HN}{AB.AC}\)
\(\begin{array}{l} = \frac{{HM.BH.HN.HC}}{{BH.AB.HC.AC}}\\ = \frac{{HM}}{{BH}}.\frac{{BH}}{{AB}}.\frac{{HN}}{{HC}}.\frac{{HC}}{{AC}}\\ = \cos {H_1}.\cos B.\cos {H_2}.\cos C\\ = \cos C.\cos B.\cos B.\cos C\\ = {\cos ^2}B.{\cos ^2}C\end{array}\)
Do đó ${{S}_{\Delta ABC}}=\frac{{{S}_{\Delta MHN}}}{{{\cos }^{2}}B.{{\cos }^{2}}C}$.
Bài 5 (0,5 điểm).
Bác An cắt một sợi dây thép dài \(30cm\) thành hai đoạn. Mỗi đoạn được uốn thành một hình vuông. Bác An căng vải trên hai khung đó. Hỏi cần cắt đoạn dây như thế nào để tổng diện tích phần vải căng đạt giá trị nhỏ nhất (coi mép vải thừa không đáng kể).
Phương pháp:
Giả sử sợi dây thép AC = 30cm được cắt thành hai đoạn AB và BC như hình vẽ.
Gọi cạnh của hình vuông uốn được từ đoạn AB là \(x\) (cm), \(\left( {0 < x < 30} \right)\).
Khi đó biểu diễn được độ dài đoạn AB theo công thức tính diện tích hình vuông.
Suy ra độ dài đoạn BC và độ dài cạnh của hình vuông uốn được từ đoạn BC.
Suy ra tổng diện tích hai hình vuông.
Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức cộng 1 số để xuất hiện giá trị nhỏ nhất của biểu thức.
Dấu “=” xảy ra là giá trị nhỏ nhất của tổng diện tích hai hình vuông, ta tính được \(x\).
Suy ra độ dài đoạn AB, BC và xác định được vị trí cắt thoả mãn.
Lời giải:
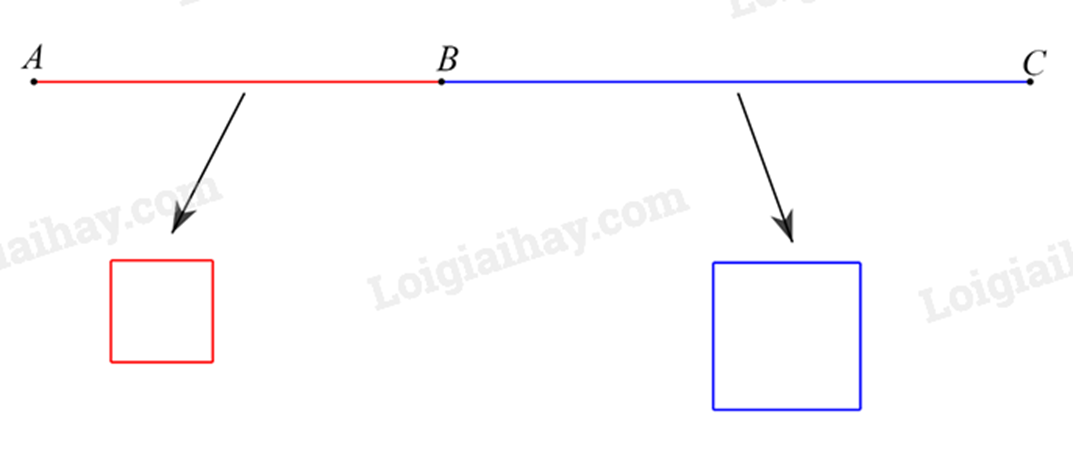
Giả sử sợi dây thép AC = 30cm được cắt thành hai đoạn AB và BC như hình vẽ.
Gọi cạnh của hình vuông uốn được từ đoạn AB là \(x\) (cm), \(\left( {0 < x < 30} \right)\).
Khi đó độ dài đoạn AB là \(4x\) (m).
Độ dài đoạn BC là: \(30 - 4x\) (m).
Suy ra độ dài cạnh hình vuông được uốn bởi đoạn BC là: \(\frac{{30 - 4x}}{4} = \frac{{15}}{2} - x\) (m).
Tổng diện tích hai hình vuông lúc này là: \({x^2} + {\left( {\frac{{15}}{2} - x} \right)^2}\) \(\left( {{m^2}} \right)\).
Ta có:
\(\begin{array}{l}{x^2} + {\left( {\frac{{15}}{2} - x} \right)^2} = {x^2} + \frac{{225}}{4} - 15x + {x^2}\\ = 2{x^2} - 15x + \frac{{225}}{4}\\ = 2\left( {{x^2} - \frac{{15}}{2}x + \frac{{225}}{{16}}} \right) + \frac{{225}}{8}\\ = 2{\left( {x - \frac{{15}}{4}} \right)^2} + \frac{{225}}{8} \ge \frac{{225}}{8}\end{array}\)
Dấu “=” xảy ra là giá trị nhỏ nhất của tổng diện tích hai hình vuông.
Khi đó \(x - \frac{{15}}{4} = 0\), suy ra \(x = \frac{{15}}{4}\)
Khi đó độ dài đoạn thẳng AB = \(\frac{{15}}{4}.4 = 15\) (cm) và độ dài BC = 30 – 15 = 15 (cm) hay B là trung điểm của AC.
Vậy để tổng diện tích hai hình vuông đạt giá trị nhỏ nhất thì ta chia đoạn dây thép thành hai phần bằng nhau và bằng 15cm.
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5












Danh sách bình luận