Một công viên lớn đang được thiết kế với một khu vực trồng hoa theo kiểu hình học. Khu vực này có dạng hình tam giác đều với diện tích 900 \({m^2}\), bên trong có 10 bồn hoa hình tròn tiếp xúc với các cạnh của tam giác như hình vẽ. Ở bồn hoa trung tâm, người ta trồng hoa hồng với chi phí trồng là 200 nghìn đồng cho mỗi mét vuông. Ở các bồn còn lại thì trồng hoa cúc với chi phí trồng là 100 nghìn đồng cho mỗi mét vuông. Hỏi chi phí trồng hoa ở tất cả các bồn là bao nhiêu triệu đồng (kết quả được làm tròn đến hàng đơn vị)?
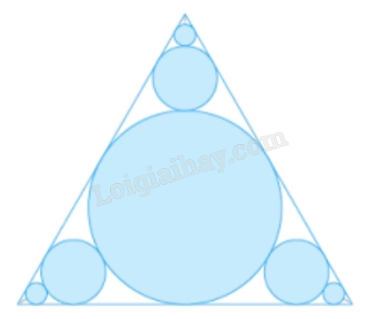
Tính bán kính các đường tròn, từ đó tính diện tích.
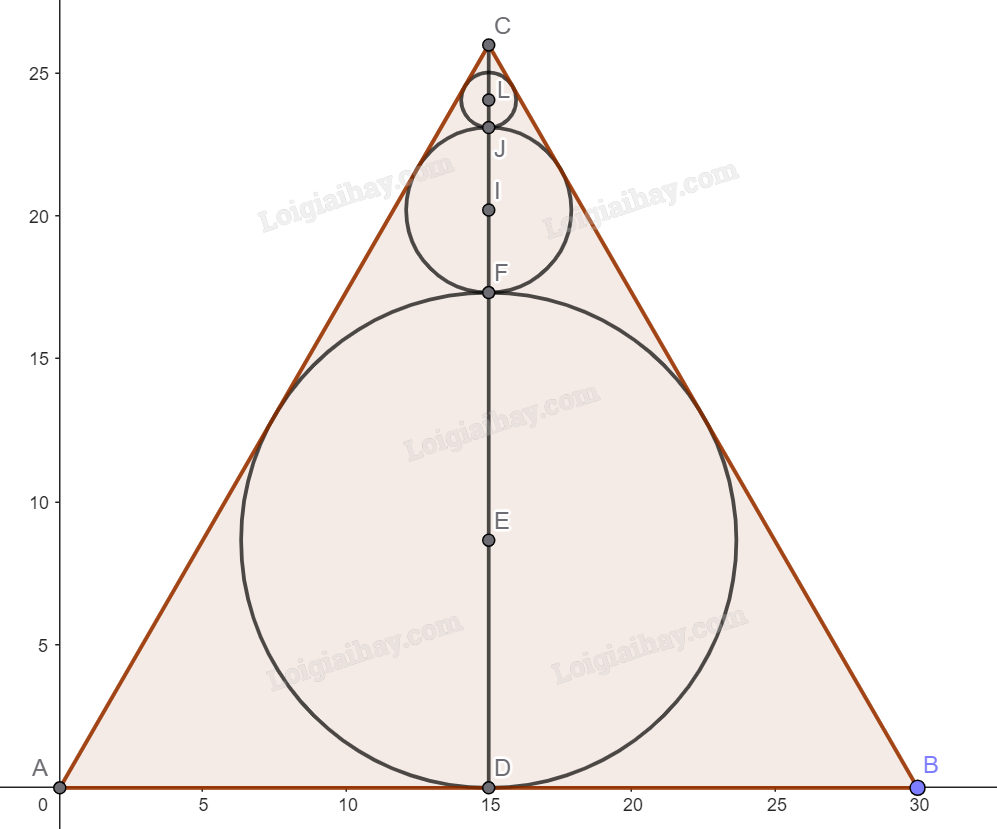
Gọi tên các điểm như hình vẽ, gọi các đường tròn có kích thước từ lớn đến nhỏ là \(\left( {{C_1}} \right)\), \(\left( {{C_2}} \right)\), \(\left( {{C_3}} \right)\).
Gọi độ dài cạnh tam giác đều ABC là a (m).
Tam giác ABC đều diện tích \(\frac{{{a^2}\sqrt 3 }}{4} = 900 \Leftrightarrow a = \frac{{60}}{{\sqrt[4]{3}}}\).
Ta có: \(CD = \frac{{a\sqrt 3 }}{2} = \frac{{60}}{{\sqrt[4]{3}}}.\frac{{\sqrt 3 }}{2} = \frac{{30}}{{\sqrt[3]{3}}}\); \(ED = \frac{{CD}}{3} = \frac{{10}}{{\sqrt[3]{3}}}\).
Diện tích \(\left( {{C_1}} \right)\) là \({S_1} = \pi {\left( {\frac{{10}}{{\sqrt[3]{3}}}} \right)^2} = \pi \frac{{100}}{{\sqrt[3]{9}}}\).
Ta có: \(CF = ED = \frac{{10}}{{\sqrt[3]{3}}}\); \(IF = \frac{{CF}}{3} = \frac{{10}}{{3\sqrt[3]{3}}}\).
Diện tích \(\left( {{C_2}} \right)\) là \({S_2} = \pi {\left( {\frac{{10}}{{3\sqrt[3]{3}}}} \right)^2} = \pi \frac{{100}}{{9\sqrt[3]{9}}}\).
Ta có: \(CJ = IF = \frac{{10}}{{3\sqrt[3]{3}}}\); \(LJ = \frac{{CJ}}{3} = \frac{{10}}{{9\sqrt[3]{3}}}\).
Diện tích \(\left( {{C_3}} \right)\) là \({S_3} = \pi {\left( {\frac{{10}}{{9\sqrt[3]{3}}}} \right)^2} = \pi \frac{{100}}{{81\sqrt[3]{9}}}\).
Chi phí trồng hoa là:
\(200000.{S_1} + 100000.(3{S_2} + 3{S_3}) \approx 35800182\) đồng \( \approx 36\) triệu đồng.
Các bài tập cùng chuyên đề
Trong không gian Oxyz, cho \(A\left( {0;2;1} \right),B\left( {3; - 2;1} \right)\) và \(C\left( { - 2;5;7} \right)\).
a) Tính chu vi của tam giác ABC.
b) Tính \(\widehat {BAC}\).
Cho các điểm A(–1; –1; 0), B(0; 3; –1), C(–1; 14; 0), D(–3; 6; 2). Chứng minh rằng ABCD là hình thang.
Cho hình hộp ABCD.A′B′C′D′ có A(1; 0; 1), B(2; 1; 2), D(1; –1; 1), C′(4; 5; –5). Tìm toạ độ các đỉnh còn lại của hình hộp.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O.
Trong không gian Oxyz, cho vecto \(\overrightarrow a = (1;2;3)\), \(\overrightarrow b = (3;6;9)\).
Cho điểm \(A\left( {3; - 1;1} \right)\). Hình chiếu vuông góc của điểm \(A\) trên mặt phẳng \(\left( {Oyz} \right)\) là điểm
A. \(M\left( {3;0;0} \right)\).
B. \(N\left( {0; - 1;1} \right)\).
C. \(P\left( {0; - 1;0} \right)\).
D. \(Q\left( {0;0;1} \right)\).
Cho điểm \(M\left( { - 3;2; - 1} \right)\) và điểm \(M'\) là điểm đối xứng của \(M\) qua mặt phẳng \(\left( {Oxy} \right)\). Toạ độ của điểm \(M'\) là
A. \(\left( { - 3;2;1} \right)\).
B. \(\left( {3;2;1} \right)\).
C. \(\left( {3;2; - 1} \right)\).
D. \(\left( {3; - 2; - 1} \right)\).
Hình chiếu vuông góc của điểm \(M\left( {2;1; - 1} \right)\) trên trục \(Oz\) có toạ độ là
A. \(\left( {2;1;0} \right)\).
B. \(\left( {0;0; - 1} \right)\).
C. \(\left( {2;0;0} \right)\).
D. \(\left( {0;1;0} \right)\).
Cho điểm \(A\left( { - 3;1;2} \right)\) và điểm \(A'\) là điểm đối xứng của \(A\) qua trục \(Oy\). Toạ độ của điểm \(A'\) là
A. \(\left( {3; - 1; - 2} \right)\).
B. \(\left( {3; - 1;2} \right)\).
C. \(\left( {3;1; - 2} \right)\).
D. \(\left( { - 3; - 1;2} \right)\).
Khối rubik như hình vẽ có độ dài cạnh bằng 2. Khi gắn rubik vào hệ trục tọa độ trong không gian Oxyz, cho hình lập phương ABCD.A’B’C’D’ có A(0;0;0), B(2;0;0), D(0;2;0), A’(0;0;2). Gọi M, N lần lượt là trung điểm của CD, AA’ (xem hình vẽ bên dưới). Biết rằng cos[B,MN,D’] = m, tính giá trị 14m.
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’, biết rằng A(1;2;0), A’(1;0;1), B(1;5;1), D’(0;-2;0).
