Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
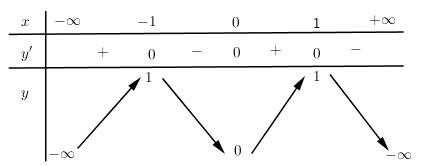
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
-
A.
$y = {x^4} - 2{x^2}$
-
B.
$y = - {x^4} + 2{x^2}$
-
C.
$y = - {x^4} - 2{x^2} - 3$
-
D.
$y = - {x^4} - 2{x^2} + 1$
- Nhận xét dáng đồ thị suy ra hệ số $a$.
- Tìm điểm đi qua và đối chiếu các đáp án
Nhận xét: Dễ thấy bảng biến thiên của đồ thị hàm số bậc 4.
Ngoài cùng bên phải của $y' < 0 \Rightarrow a < 0 \Rightarrow $Loại đáp án A
Thay điểm $\left( {0;0} \right)$ vào các hàm số ở đáp án B, C, D
Điểm $\left( {0;0} \right)$ chỉ thuộc vào đồ thị hàm số $y = - {x^4} + 2{x^2}$
Đáp án : B
Các bài tập cùng chuyên đề
Hàm số nào sau đây có thể có đồ thị dạng như hình vẽ?
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
Hàm số nào sau đây có đồ thị như hình vẽ?
Hàm số nào có thể có đồ thị dạng như hình vẽ?
Hàm số nào sau đây có đồ thị như hình vẽ?
Đồ thị bên là đồ thị của hàm số nào trong các hàm số sau:
Đồ thị sau đây là của hàm số nào?
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Cho hàm số $y = f\left( x \right)$ xác định liên tục trên R có bảng biến thiên:
Khẳng định nào sau đây là đúng?
Cho hàm số $y = f\left( x \right) = a{x^4} + {b^2}{x^2} + 1\left( {a \ne 0} \right)$ . Trong các khẳng định dưới đây, khẳng định nào là đúng?
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng?
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
Cho hàm số $y = a{x^3} + b{x^2} + cx + d\,\left( {a \ne 0} \right)$ có đồ thị hàm số như hình vẽ dưới đây. Khẳng định nào sau đây về dấu của $a,b,c,d$ là đúng nhất?
Hàm số $y = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?
Hàm số $y = a{x^4} + b{x^2} + c$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
Đồ thị hàm số bên là đồ thị của hàm số $y = {x^4} - 4{x^2} + 1\left( C \right).$ Tìm $m$ để phương trình ${x^4} - 4{x^2} + 1 - m = 0$ có $4$ nghiệm phân biệt
Cho hàm số $y = - {x^4} + 2{{\text{x}}^2} + 1$ có đồ thị như hình dưới. Tìm tất cả các giá trị thực của tham số $m$ để phương trình $ - {x^4} + 2{{\text{x}}^2} + 1 = m$ có bốn nghiệm phân biệt.
Cho hàm số $y = f(x)$ liên tục và có đạo hàm cấp hai trên $R$. Đồ thị của các hàm số $y = f(x),y = f'(x),y = f''(x)$ lần lượt là các đường cong nào trong hình vẽ bên.
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên sau:
Đồ thị nào trong các phương án A, B, C, D thể hiện hàm số \(y = f\left( x \right)\)?
Cho các dạng đồ thị (I), (II), (III) như hình dưới đây:
Liệt kê tất cả các dạng có thể biểu diễn đồ thị hàm số \(y = {x^3} + b{x^2} - x + d\).
