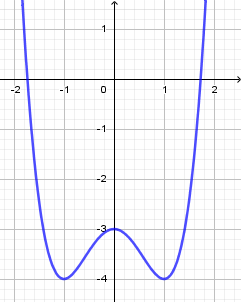
Đồ thị sau đây là của hàm số nào?
-
A.
$y = {x^4} - 2{x^2} - 3$
-
B.
$y = - \dfrac{1}{4}{x^4} + 3{x^2} - 3$
-
C.
$y = {x^4} - 3{x^2} - 3$
-
D.
$y = {x^4} + 2{x^2} - 3$
Quan sát đồ thị và tìm các điểm cực trị, đối chiếu với các đáp án bài cho.
Từ đồ thị của hàm số ta dễ dàng thấy được:
Điểm cực tiểu $\left( { - 1; - 4} \right),\left( {1; - 4} \right)$ và điểm cực đại $\left( {0; - 3} \right)$
Xét Đáp án A: $y' = 4{x^3} - 4x = 4x\left( {{x^2} - 1} \right)$ có các nghiệm $x = 0;x = \pm 1$.
Do đó đồ thị có các điểm cực tiểu là $\left( { - 1; - 4} \right),\left( {1; - 4} \right)$ và điểm cực đại là $\left( {0; - 3} \right)$.
Đáp án : A
HS có thể làm nhanh bằng cách loại trừ phương án: nhận xét dạng đồ thị suy ra hệ số $a > 0$ nên loại B, sau đó giải các phương trình $y' = 0$ ở 3 đáp án còn lại, đáp án nào có 3 nghiệm phân biệt $x = 0;x = \pm 1$ thì chọn.
