Đề bài
Hàm số nào sau đây có đồ thị như hình vẽ?
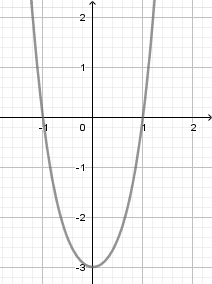
-
A.
$y = - {x^4} - 2{x^2} + 3$
-
B.
$y = {x^4} - 2{x^2} - 3$
-
C.
$y = - {x^4} - 2{x^2} - 3$
-
D.
$y = {x^4} + 2{x^2} - 3$
Phương pháp giải
Quan sát đồ thị hàm số và nhận xét dáng điệu đồ thị, điểm cực đại, cực tiểu, đối chiếu các đáp án đã cho.
Lời giải của GV Loigiaihay.com
Từ dáng đồ thị ta có $a > 0$ nên loại A, C
Đồ thị hàm số có điểm cực tiểu là $\left( {0; - 3} \right).$
Do hàm số chỉ có một điểm cực trị nên $y' = 0$ phải có duy nhất một nghiệm ${x_0}$ và $y\left( {{x_0}} \right) = - 3.$
Kiểm tra ta chỉ thấy đáp án D là phù hợp.
Ngoài ra, đáp án B bị loại vì phương trình $y'=0$ ở đáp án B có $3$ nghiệm phân biệt.
Đáp án : D








Danh sách bình luận