Đề bài
Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} = - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:
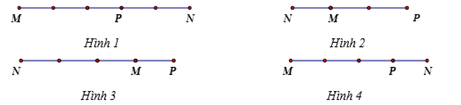
-
A.
Hình 1.
-
B.
Hình 2
-
C.
Hình 3
-
D.
Hình 4
Lời giải của GV Loigiaihay.com
Ta có \(\overrightarrow {MN} = - 3\overrightarrow {MP} \) nên \(MN = 3MP\) và\(\overrightarrow {MN} \) và \(\overrightarrow {MP} \) ngược hướng.
Đáp án : C








Danh sách bình luận