Bài 8.9 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của AC và BD và SA=SC, SB= SD.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của AC và BD và SA=SC, SB= SD. Chứng minh \(BC \bot SO\) và \(SC \bot BD\).
Phương pháp giải - Xem chi tiết
Chứng minh \(SO \bot AC,SO \bot BD\) từ đó suy ra \(SO \bot \left( {ABCD} \right)\) và suy ra \(SO \bot BC\)
Chứng minh \(BD \bot \left( {SAC} \right)\) từ đó suy ra \(BD \bot SC\)
Lời giải chi tiết
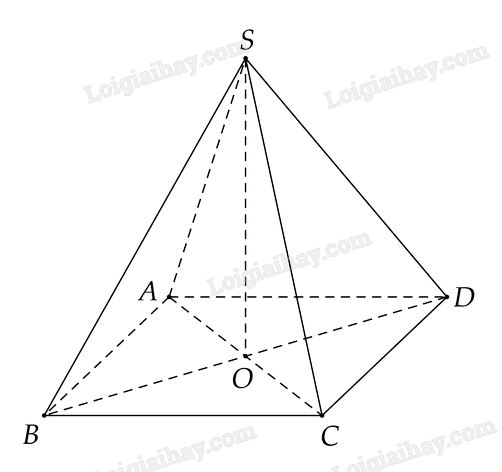
+) Vì \(ABCD\) là hình thoi nên \(AC \bot BD\) tại trung điểm \(O\) của mỗi đường
Vì \(SA = SC \Rightarrow \Delta SAC\) cân tại \(S\) và \(O\) là trung điểm \(AC\) nên \(SO \bot AC\)
Vì \(SB = SD\)\( \Rightarrow \Delta SBD\) cân tại \(S\) và \(O\) là trung điểm \(BD\) nên \(SO \bot BD\)
Ta có \(\left\{ \begin{array}{l}SO \bot AC\\SO \bot BD\end{array} \right. \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot BC\)
+) Vì \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot BD\)
Ta có \(\left\{ \begin{array}{l}SO \bot BD\\AC \bot BD\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)
Các bài khác cùng chuyên mục
- Bài 4.20 trang 114 SGK Toán 11 tập 1 - Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá













Danh sách bình luận