Bài 2, Đường thẳng vuông góc với mặt phẳng. Phép chiếu ..

Bài 8.8 trang 63 SGK Toán 11 tập 2 - Cùng khám phá

Cho tứ diện ABCD biết ABC và BCD là hai tam giác cân có chung cạnh đáy BC . Gọi I là trung điểm cạnh BC. Chứng minh \(BC \bot (ADI)\).

Đề bài

Cho tứ diện ABCD biết ABC và BCD là hai tam giác cân có chung cạnh đáy BC . Gọi I là trung điểm cạnh BC. Chứng minh \(BC \bot (ADI)\).

Phương pháp giải - Xem chi tiết

Dựa vào tam giác cân để suy ra \(AI \bot BC\) và \(DI \bot BC\)

Lời giải chi tiết

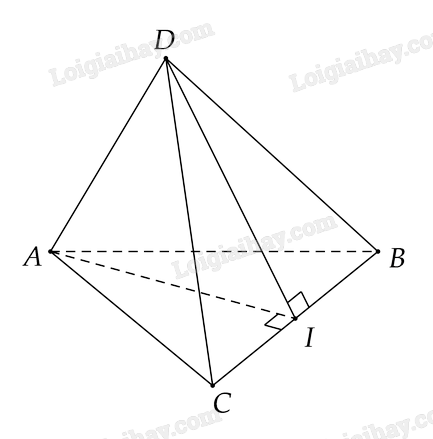
Vì \(\Delta ABC\) cân tại \(A\) và \(I\) là trung điểm của \(BC\) nên \(AI \bot BC\)

Vì \(\Delta DBC\) cân tại \(D\) và \(I\) là trung điểm của \(BC\) nên \(DI \bot BC\)

Ta có \(\left\{ \begin{array}{l}BC \bot AI\\BC \bot DI\end{array} \right. \Rightarrow BC \bot \left( {AID} \right)\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 8.9 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của AC và BD và SA=SC, SB= SD.
Bài 8.10 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Một cây ăng-ten thẳng đứng với mặt đất và được buộc giằng bởi 4 dây cáp từ một điểm B cách chân A của ăng-ten 4 mét . Khoảng cách từ A đến chân buộc dây giằng bằng 3m ( Hình 8.27).
Bài 8.11 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a
Bài 8.12 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc mặt đáy và \(SA = \sqrt 2 .a\).
Bài 8.7 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình chóp S.ABCD có (SA bot (ABCD)) và đáy là hình vuông. Gọi M là hình chiếu vuông góc của A trên SB. Chứng minh (AM bot (SBC)) và (BD bot SC).
Bài 8.6 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Cho hai đường thẳng phân biệt \(a,b\)và mặt phẳng \((\alpha )\), trong đó \(a \bot (\alpha )\).Mỗi mệnh đề sau đúng hay sai? Vì sao?
Bài 8.5 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Mỗi mệnh đề sau đúng hay sai? Vì sao?
Giải mục 4 trang 62 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot \left( {ABCD} \right)\).
Giải mục 3 trang 60, 61, 62 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình hộp \(ABCD.A'B'C'D'\). Tìm hình chiều của các điểm \(A',C',D'\) lên mặt phẳng \(\left( {ABCD} \right)\) theo phương của đường thẳng \(BB'\)
Giải mục 2 trang 56, 57, 58, 59, 60 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot AB\) và \(A'A \bot AD\) (Hình 8.8)
Giải mục 1 trang 55, 56 SGK Toán 11 tập 2 - Cùng khám phá
Quan sát hình ảnh cây cột và nền nhà (Hình 8.6). Xem nền nhà là hình ảnh của mặt phẳng \(\left( \alpha \right)\).
Lý thuyết Đường thẳng vuông góc với mặt phẳng. Phép chiếu vuông góc - SGK Toán 11 Cùng khám phá
A. Lý thuyết 1. Đường thẳng vuông góc với mặt phẳng a) Khái niệm