 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Ôn tập chương IV: Biểu thức đại số
Ôn tập chương IV: Biểu thức đại số
Bài 63 trang 50 SGK Toán 7 tập 2
Cho đa thức:
Video hướng dẫn giải
Cho đa thức: \(M(x) = 5{{\rm{x}}^3} + 2{{\rm{x}}^4} - {x^2} + 3{{\rm{x}}^2} - {x^3}\)\( - {x^4} + 1 - 4{{\rm{x}}^3}\)
LG a
Sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.
Phương pháp giải:
Thu gọn đa thức \(M(x)\) sau đó sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.
Lời giải chi tiết:
Rút gọn:
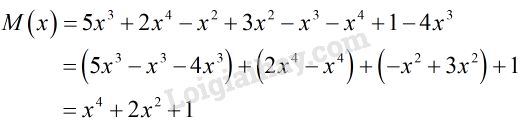
Sắp xếp các hạng tử của đa thức \(M(x)\) theo lũy thừa giảm của biến:
\(M(x)={x^4} + 2{x^2} + 1\)
LG b
Tính \(M(1)\) và \(M(-1)\)
Phương pháp giải:
Thay giá trị tương ứng của \(x\) vào đa thức sau khi đã rút gọn rồi tính giá trị của đa thức đó.
Lời giải chi tiết:
Ta có: \(M(x)={x^4} + 2{x^2} + 1\)
Nên:
\(M\left( 1 \right) = {1^4} + {2.1^2} + 1 = 4\)
\(M\left( { - 1} \right) = {\left( { - 1} \right)^4} + 2.{\left( { - 1} \right)^2} + 1 = 4\)
LG c
Chứng tỏ rằng đa thức trên không có nghiệm.
Phương pháp giải:
Đa thức không có nghiệm khi và chỉ khi đa thức đó luôn khác \(0\) với mọi \(x\).
Lời giải chi tiết:
Ta có: \(M\left( x \right) = {x^4} + 2{x^2} + 1\)
Vì \({x^4} \ge 0\) với mọi \(x\, \in\mathbb R\)
và \({x^2} \ge 0\) với mọi \(x\, \in\mathbb R\)
\(\;\Rightarrow {x^4} + 2{x^2} + 1 \ge 1> 0\) với mọi \(x\, \in\mathbb R\)
\(\Rightarrow M\left( x \right)\) không có nghiệm.
Loigiaihay.com












Danh sách bình luận