Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Ôn tập chương IV: Biểu thức đại số
Bài 62 trang 50 SGK Toán 7 tập 2
Cho hai đa thức:
Video hướng dẫn giải
Cho hai đa thức:
\(P\left( x \right) = {x^5} - 3{x^2} + 7{x^4} - 9{x^3} + {x^2} \)\(- \dfrac{1}{4}x\)
\(Q\left( x \right) = 5{x^4} - {x^5} + {x^2} - 2{x^3} + 3{x^2}\)\( - \dfrac{1}{4}\)
LG a
Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến.
Phương pháp giải:
Thu gọn và sắp xếp mỗi đa thức trên theo lũy thừa giảm của biến.
Lời giải chi tiết:
Ta có:
\(P\left( x \right) = {x^5} - 3{x^2} + 7{x^4} - 9{x^3} + {x^2} \)\(- \dfrac{1}{4}x\)
\( = {x^5} + 7{x^4} - 9{x^3} + \left( { - 3{x^2} + {x^2}} \right) \)\(\,- \dfrac{1}{4}x\)
\( = {x^5} + 7{x^4} - 9{x^3} - 2{x^2} - \dfrac{1}{4}x\)
\(Q\left( x \right) = 5{x^4} - {x^5} + {x^2} - 2{x^3} + 3{x^2}\)\( - \dfrac{1}{4}\)
\( = - {x^5} + 5{x^4} - 2{x^3} + \left( {{x^2} + 3{x^2}} \right) - \dfrac{1}{4}\)
\( = - {x^5} + 5{x^4} - 2{x^3} + 4{x^2} - \dfrac{1}{4}\)
LG b
Tính \(P(x) + Q(x)\) và \(P(x) - Q(x)\).
Phương pháp giải:
- Áp dụng qui tắc cộng, trừ đa thức một biến.
Lời giải chi tiết:
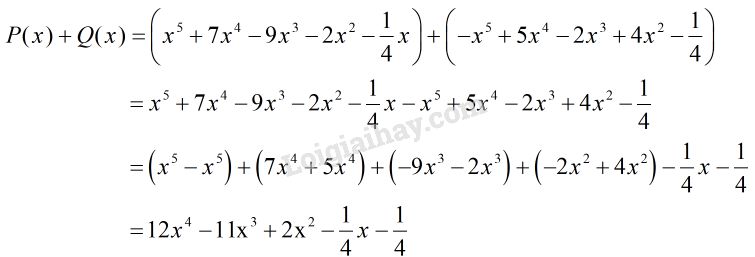
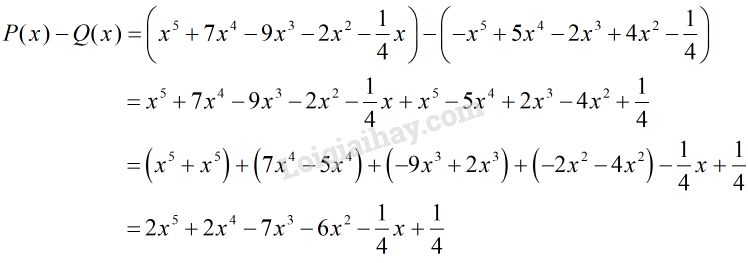
Cách khác:
LG c
Chứng tỏ rằng \(x = 0\) là nghiệm của đa thức \(P(x)\) nhưng không phải là nghiệm của đa thức \(Q(x)\).
Phương pháp giải:
- Muốn kiểm tra một số \(a\) có phải là nghiệm của đa thức \(f(x)\) không ta làm như sau:
- Tính \(f(a)=?\) ( giá trị của \(f(x)\) tại \(x = a\))
+) Nếu \(f(a)= 0 \) \(\Rightarrow\) \( a\) là nghiệm của \(f(x)\)
+) Nếu \(f(a)≠0\) \( \Rightarrow \) \(a\) không phải là nghiệm của \(f(x)\).
Lời giải chi tiết:
Ta có:
\( P(x)= {x^5} + 7{x^4} - 9{x^3} - 2{x^2} - \dfrac{1}{4}x\)
Nên \(P\left( 0 \right) = {0^5} + {7.0^4} - {9.0^3} - {2.0^2} - \dfrac{1}{4}.0\)\(\,=0\)
\( \Rightarrow x = 0\) là nghiệm của \(P(x)\).
Ta có: \( Q(x) = - {x^5} + 5{x^4} - 2{x^3} + 4{x^2} - \dfrac{1}{4}\)
Nên \(Q\left( 0 \right) = - {0^5} + {5.0^4} - {2.0^3} + {4.0^2} - \dfrac{1}{4}\)\( = - \dfrac{1}{4} \ne 0\)
\( \Rightarrow x = 0\) không phải là nghiệm của \(Q(x)\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 63 trang 50 SGK Toán 7 tập 2
- Bài 64 trang 50 SGK Toán 7 tập 2
- Bài 65 trang 51 SGK Toán 7 tập 2
- Lý thuyết Ôn tập chương 4. Biểu thức đại số
- Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 4 – Đại số 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
