-
Toán 11 tập 1 - Cùng khám phá
-
Giải Toán 11 tập 2 - Cùng khám phá
Bài 6.13 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
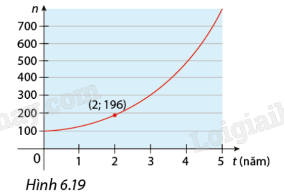
Lúc đầu trong ao có một số con ếch. Người ta ghi nhận số lượng ếch trong 5 năm đầu như Hình 6.19. Giả sử số lượng ếch tăng theo hàm số \(n\left( t \right) = C.{a^t}\).
Đề bài
Lúc đầu trong ao có một số con ếch. Người ta ghi nhận số lượng ếch trong 5 năm đầu như Hình 6.19. Giả sử số lượng ếch tăng theo hàm số \(n\left( t \right) = C.{a^t}\).
a) Tính số lượng ếch lúc ban đầu.
b) Tìm hàm số biểu diễn số lượng ếch sau t năm kể từ khi chúng xuất hiện trong ao.
c) Dự đoán số lượng ếch sau 15 năm.
Phương pháp giải - Xem chi tiết
a) Số lượng ếch ban đầu là n khi t = 0.
b) Dựa vào các điểm thuộc đồ thị để tìm C, a.
Số lượng ếch mỗi năm bằng số lượng ếch ban đầu cộng với số lượng ếch tăng theo hàm số \(n\left( t \right) = C.{a^t}\).
c) Thay t = 15 vào hàm số tìm được ở phần b.
Lời giải chi tiết
a) Số lượng ếch ban đầu là 100 con.
b) Đồ thị hàm số đi qua 2 điểm (0; 100) và (2; 196). Ta có:
\(\left\{ \begin{array}{l}C.{a^0} = 100\\C.{a^2} = 196\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C = 100\\{a^2} = 1,96\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C = 100\\a = 1,4\end{array} \right.\)
\( \Rightarrow n\left( t \right) = 100.1,{4^t}\)
Vậy hàm số biểu diễn số lượng ếch sau t năm kể từ khi chúng xuất hiện trong ao là:
\(H\left( t \right) = 100 + 100.1,{4^t}\)
c) \(H\left( {15} \right) = 100 + 100.1,{4^{15}} \approx 15656\) (con).
Bình luận
Chia sẻ
- Bài 6.12 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 6.11 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 6.10 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 2 trang 17, 18, 19 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 1 trang 14, 15 SGK Toán 11 tập 2 - Cùng khám phá
>> Xem thêm
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
