Bài 6 trang 79 SGK Đại số 10
Trong mặt phẳng tọa độ Oxy, trên các tia Ox, Oy...
Đề bài
Trong mặt phẳng tọa độ \(Oxy\), trên các tia \(Ox, Oy\) lần lượt lấy các điểm \(A\) và \(B\) thay đổi sao cho đường thẳng \(AB\) luôn tiếp xúc với đường tròn tâm \(O\) bán kính \(1\). Xác định tọa độ của \(A\) và \(B\) để đoạn \(AB\) có độ dài nhỏ nhất.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng hệ quả: Hai số dương bất kì có tích không đổi thì tổng đạt giá trị nhỏ nhất khi hai số bằng nhau.
BĐT Cô si: Cho hai số dương a, b. Khi đó \(a + b \ge 2\sqrt {ab} \).
Dấu "=" xảy ra khi \(a=b\).
Lời giải chi tiết
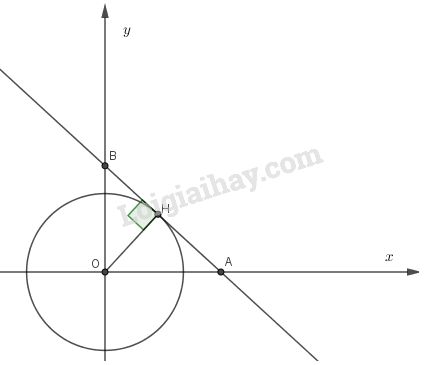
Tam giác AOB vuông tại O có OH là đường cao nên \(HA.HB = O{H^2} = {1^2} = 1\)
Áp dụng bất đẳng thức Cô si ta có:
\(AB = AH + HB \ge 2\sqrt {AH.HB} \) \(= 2\sqrt 1 = 2\)
\(\Rightarrow A{B_{\min }} = 2 \Leftrightarrow HA = HB = 1\)
\(∆OAB\) có OH vừa là đường cao vừa là đường trung tuyến nên vuông cân: \(OA = OB\) và \(AB = 2\).
Áp dụng định lý Pitago cho tam giác vuông OAB ta có:
\(\begin{array}{l}
O{A^2} + O{B^2} = A{B^2}\\
\Leftrightarrow O{A^2} + O{A^2} = A{B^2}\\
\Leftrightarrow 2O{A^2} = {2^2}\\
\Leftrightarrow O{A^2} = 2\\
\Leftrightarrow OA = \sqrt 2
\end{array}\)
Mà A nằm trên tia Ox nên \(A(\sqrt 2; 0)\).
Lại có OB=OA nên \(OB = \sqrt 2 \).
Mà B nằm trên tia Oy nên \(B(0; \sqrt2)\).
Vậy \(A(\sqrt 2; 0)\) và \(B(0; \sqrt2)\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 5 trang 79 SGK Đại số 10
- Bài 4 trang 79 SGK Đại số 10
- Bài 3 trang 79 SGK Đại số 10
- Bài 2 trang 79 SGK Đại số 10
- Bài 1 trang 79 SGK Đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
