Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 8. Tính chất ba đường trung trực của tam giác
Bài 52 trang 79 SGK Toán 7 tập 2
Chứng minh định lí:
Đề bài
Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Trường hợp bằng nhau thứ \(2\) của hai tam giác bằng nhau.
- Định nghĩa đường trung trực của đoạn thẳng.
- Chứng minh một tam giác cân ta chứng minh tam giác đó có hai cạnh bằng nhau (hoặc hai góc bằng nhau).
Lời giải chi tiết
Ta đưa về bài toán: Cho tam giác ABC có AH vừa là đường trung tuyến đồng thời là đường trung trực ứng với cạnh BC. Chứng minh: Tam giác ABC cân tại A.
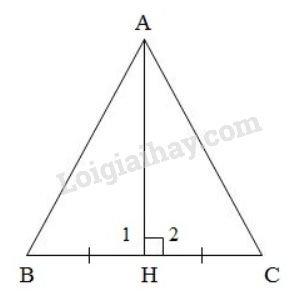
Tam giác \(ABC\) có \(AH\) là đường trung tuyến đồng thời là đường trung trực nên suy ra
\(AH ⊥ BC\) và \(HB = HC\).
Xét \(\Delta HAB\) và \(\Delta HAC\) có:
+) \(HB = HC\) (Chứng minh trên)
+) \(\widehat{H_{1}}=\widehat{H_{2}} = 90^o\)
+) \(AH\) là cạnh chung
Vậy \(∆HAB = ∆HAC\) (c.g.c)
\( \Rightarrow AB = AC\) (Hai cạnh tương ứng)
Vậy \(∆ABC\) cân tại \(A\) (điều phải chứng minh).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 53 trang 80 SGK Toán 7 tập 2
- Bài 54 trang 80 SGK Toán 7 tập 2
- Bài 55 trang 80 SGK Toán 7 tập 2
- Bài 56 trang 80 SGK Toán 7 tập 2
- Bài 57 trang 80 SGK Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
