Bài 5 trang 82 SGK Toán 7 tập 1
Vẽ góc ABC có số đo bằng:
Đề bài
a) Vẽ góc \(ABC\) có số đo bằng \(56^{\circ}.\)
b) Vẽ góc \(ABC'\) kề bù với góc \(ABC.\) Hỏi số đo của góc \(ABC'\)?
c) Vẽ góc \(C'BA'\) kề bù với góc \(ABC'\). Tính số đo của góc \(C'BA'.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
b. Áp dụng định nghĩa hai góc kề bù: Hai góc kề bù có tổng số đo bằng \(180^o\).
c. Áp dụng tính chất hai góc đối đỉnh: Hai góc đối đỉnh thình bằng nhau.
Lời giải chi tiết
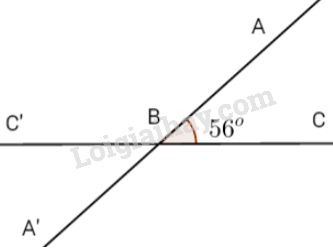
a) Sử dụng thước đo độ, ta vẽ \(\widehat{ABC}=56^{\circ}\).
b) Vẽ tia đối của tia \(BC\) ta được tia \(BC'\), được góc \(ABC'\) kề bù với góc \(ABC.\)
Ta có: \(\widehat{ABC'}+\widehat{ABC}=180^{\circ}\) (hai góc kề bù)
Suy ra \(\widehat{ABC'}=180^{\circ}-\widehat{ABC}=180^{\circ}-56^{\circ}\)\(=124^{\circ}\).
c) Vẽ tia đối của tia \(BA\), ta được tia \(BA'\), thì góc \(C'BA'\) kề bù với góc \(ABC'.\)
Ta có \(\widehat{C'BA'}=\widehat{ABC}\) (hai góc đối đỉnh) nên \(\widehat{C'BA'}=56^{\circ}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 6 trang 83 SGK Toán 7 tập 1
- Bài 7 trang 83 SGK Toán 7 tập 1
- Bài 8 trang 83 SGK Toán 7 tập 1
- Bài 9 trang 83 SGK Toán 7 tập 1
- Bài 10 trang 83 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
