Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Bài 8. Khi nào thì AM + MB = AB?
Bài 49 trang 121 SGK Toán 6 tập 1
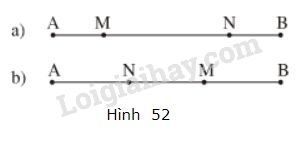
Gọi M và N là hai điểm nằm giữa hai mút của đoạn thẳng AB,Biết rẳng AN=BM. So sánh AM và BN. Xét cả hai trường hợp(h.25)
Đề bài
Gọi \(M\) và \(N\) là hai điểm nằm giữa hai mút của đoạn thẳng \(AB\). Biết rằng \(AN=BM\). So sánh \(AM\) và \(BN\). Xét cả hai trường hợp (h.52)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu điểm M nằm giữa hai điểm A và B thì \(AM + MB = AB.\)
Lời giải chi tiết
- Vì \(M\) nằm giữa hai điểm \(A\) và \(N\) nên \(AN = AM + MN\)
- Vì \(N \) nằm giữa hai điểm \(B\) và \(M\) nên \(BM = BN + MN\)
Theo đề bài: \(AN = BM\) nên \(AM + MN = BN + MN \Rightarrow AM = BN\)
(áp dụng tính chất: \(a + b = c + b \Rightarrow a = c\) )
Vậy \(AM = BN\).
- Vì \(N\) nằm giữa \(A\) và \(M\) nên \(AN + MN= AM\) \(⇒ AN = AM - MN\)
- Vì \(M\) nằm giữa \(B\) và \(N\) nên \(BM + MN= BN\) \(⇒ BM = BN - MN\)
Theo đề bài: \(AN = BM\) nên \(AM - MN=BN-MN\) \(\Rightarrow AM=BN\)
(áp dụng tính chất: \(a - b = c - b ⇒ a = c\))
Vậy \(AM = BN\).
Tóm lại: Trong cả hai trường hợp thì hai đoạn thẳng AM và BN có độ dài bằng nhau.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 50 trang 121 SGK Toán 6 tập 1
- Bài 51 trang 122 SGK Toán 6 tập 1
- Bài 52 trang 122 SGK Toán 6 tập 1
- Đề kiểm tra 15 phút - Đề số 1 - Bài 8, 9 - Chương 1 - Hình học 6
- Đề kiểm tra 15 phút - Đề số 2 - Bài 8, 9 - Chương 1 - Hình học 6
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 6 chương trình mới trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 6 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
