Phép chiếu vuông góc là gì? - Toán 11

Cho mặt phẳng (P). Quy tắc đặt tương ứng mỗi điểm M trong không gian với hình chiếu vuông góc của điểm đó lên mặt phẳng (P) được gọi là phép chiếu vuông góc lên mặt phẳng (P).

Điểm M’ được gọi là hình chiếu vuông góc (hay hình chiếu) của điểm M trên mặt phẳng (P).

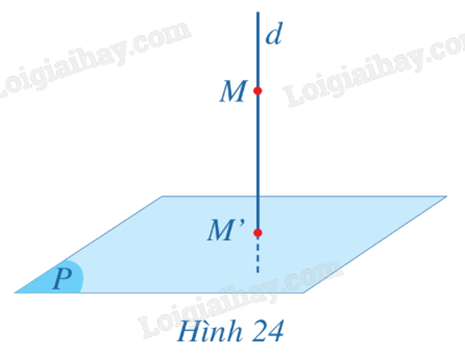
Nhận xét: Vì phép chiếu vuông góc là một trường hợp đặc biệt của phép chiếu song song (khi phương chiếu vuông góc với mặt phẳng chiếu) nên phép chiếu vuông góc có đầy đủ các tính chất của phép chiếu song song.

1) Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD và \(SA \bot (ABCD)\). Tìm hình chiếu vuông góc của SC lên mặt phẳng (ABCD) và hình chiếu vuông góc của điểm D trên mặt phẳng (SAB).

Giải:

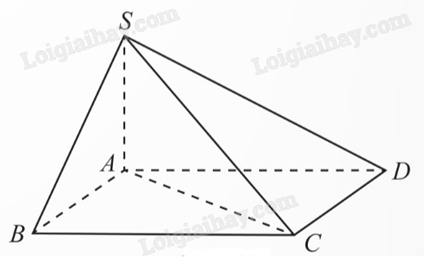
Ta có \(SA \bot (ABCD)\), suy ra AC là hình chiếu vuông góc của SC trên (ABCD).

Ta có \(SA \bot (ABCD)\), suy ra \(SA \bot AD\) (1)

Ta có ABCD là hình chữ nhật, suy ra \(AB \bot AD\) (2)

Từ (1) và (2) ta có \(AD \bot (SAB)\), suy ra A là hình chiếu vuông góc của điểm D trên (SAB).

2) Cho mặt phẳng (P) và tam giác ABC. Xác định hình chiếu tam giác ABC trên mặt phẳng (P).

Giải:

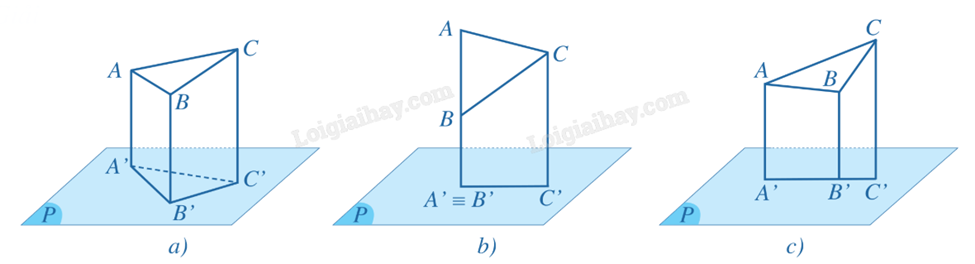
Gọi A′, B′, C′ lần lượt là hình chiếu của ba điểm A, B, C trên mặt phẳng (P).

Khi đó xảy ra các trường hợp sau:

a) Trường hợp 1: Ba điểm A′, B′, C′ không thẳng hàng. Khi đó, hình chiếu của tam giác ABC trên mặt phẳng (P) là tam giác A′B′C′.

b) Trường hợp 2: Trong ba điểm A′, B′, C′, có hai điểm trùng nhau. Chẳng hạn, điểm A′ trùng với điểm B′. Khi đó, hình chiếu của tam giác ABC trên mặt phẳng (P) là đoạn thẳng A′C′.

c) Trường hợp 3: Ba điểm A′, B′, C′ thẳng hàng. Trong ba điểm A′, B′, C′ thẳng hàng, có một điểm nằm giữa hai điểm còn lại. Chẳng hạn, điểm B′ nằm giữa hai điểm A′ và C′. Khi đó, hình chiếu của tam giác ABC trên mặt phẳng (P) là đoạn thẳng A′C′.