Hai mặt phẳng vuông góc. Cách chứng minh hai mặt phẳng vuông góc - Toán 11

Hai mặt phẳng (P) và (Q) được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^o}\).

Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này vuông chứa một đường thẳng vuông góc với mặt phẳng kia.

Chứng minh:

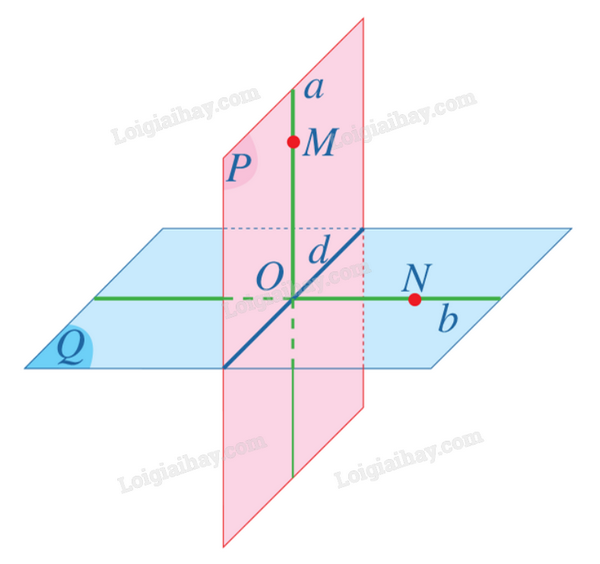
Giả sử có hai mặt phẳng (P) và (Q) thoả mãn \(a \subseteq (P)\) và \(a \bot (Q)\). Gọi O là giao điểm của a và (Q).

Do hai mặt phẳng (P) và (Q) cùng chứa O nên hai mặt phẳng đó cắt nhau theo giao tuyến d đi qua O. Trong mặt phẳng (Q), qua O kẻ đường thẳng b vuông góc với d. Lấy hai điểm M, N lần lượt thuộc các đường thẳng a, b. Ta thấy đường thẳng d vuông góc với hai tia OM, ON, suy ra góc \(\widehat {MON}\) là góc phẳng nhị diện của góc nhị diện [M, d, N]. Do \(a \bot (Q),ON \subset (Q)\) nên \(a \bot ON\), suy ra \(\widehat {MON} = {90^o}\). Vì thế, góc nhị diện [M, d, N] là góc nhị diện vuông hay \((P) \bot (Q)\).

1) Cho hình chóp S.ABCD có ABCD là hình thoi, AC cắt BD tại O và \(SO \bot (ABCD)\). Chứng minh rằng \((SAC) \bot (SBD)\).

Giải:

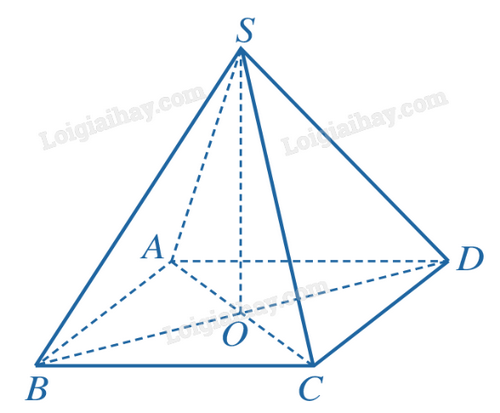
Ta thấy: Góc AOB là góc phẳng nhị diện của góc nhị diện [A, SO, B]. Do \(OA \bot OB\) nên \(AOB = {90^o}\). Vì vậy góc nhị diện [A, SO, B] là góc nhị diện vuông. Hai mặt phẳng (SAC), (SBD) cắt nhau tạo nên bốn góc nhị diện, trong đó góc nhị diện [A, SO, B] là góc nhị diện vuông nên \((SAC) \bot (SBD)\).

2) Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau. Chứng minh rằng các mặt phẳng (ABC), (BAD), (CAD) đôi một vuông góc với nhau.

Giải:

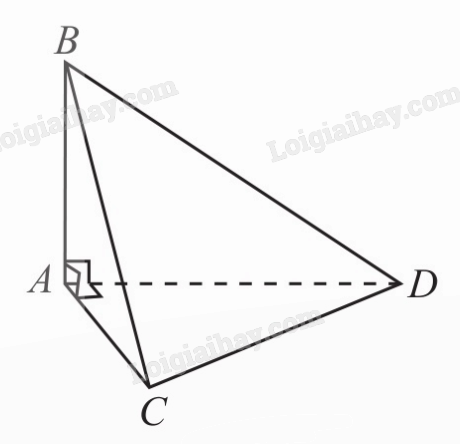
Ta có \(AB \bot AC\), \(AB \bot AD \Rightarrow AB \bot (CAD)\)

\( \Rightarrow (ABC) \bot (CAD)\), \((BAD) \bot (CAD)\).

Tương tự ta cũng có \(CA \bot AB\), \(CA \bot AD\)

\( \Rightarrow CA \bot (BAD) \Rightarrow (CAD) \bot (BAD)\).

Vậy các mặt phẳng (ABC), (BAD), (CAD) từng đôi một vuông góc với nhau.

3) Cho hình chóp S.ABCD có \(SA \bot (ABCD)\), đáy ABCD là hình chữ nhật. Chứng minh rằng:

a) \((SAB) \bot (ABCD)\);

b) \((SAB) \bot (SAD)\).

Giải:

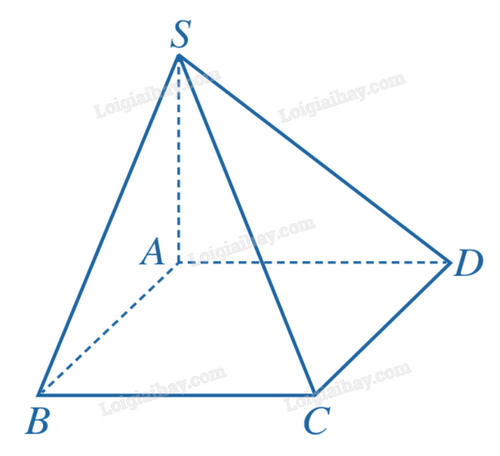
a) Do \(SA \bot (ABCD)\), \(SA \subset (SAB)\) nên \((SAB) \bot (ABCD)\).

b) Vì \(SA \bot (ABCD)\), \(AB \subset (ABCD)\) nên \(SA \bot AB\).

Do AB vuông góc với hai đường thẳng SA và AD cắt nhau trong mặt phẳng \((SAD)\) nên \(AB \bot (SAD)\). Ta có: \(AB \bot (SAD)\), \(AB \subset (SAB)\) nên \((SAB) \bot (SAD)\).

a) Tính chất 1:

Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.

Chứng minh:

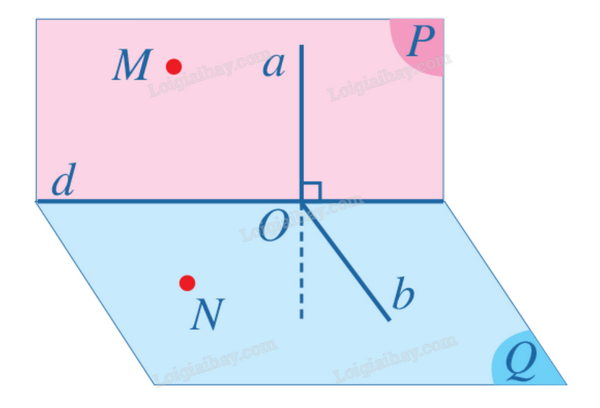
Cho hai mặt phẳng (P), (Q) vuông góc với nhau và cắt nhau theo giao tuyến d. Cho đường thẳng \(a \subset (P)\) sao cho \(a \bot d\). Gọi O là giao điểm của a và d.

Lấy hai điểm M, N lần lượt trên hai mặt phẳng (P), (Q) sao cho M, N không thuộc đường thẳng d. Ta có thể coi góc aOb là góc phẳng nhị diện của góc nhị diện [M, d, N].

Do góc nhị diện đó là góc nhị diện vuông nên \(\widehat {aOb} = {90^o}\), tức là \(a \bot Ob\). Đường thẳng a vuông góc với hai đường thẳng cắt nhau của mặt phẳng (Q) là d và Ob nên \(a \bot (Q)\).

Ví dụ minh hoạ:

Cho hình chóp S.ABCD có \((SAB) \bot (ABCD)\), đáy ABCD là hình chữ nhật. Chứng minh rằng: \((SBC) \bot (SAB)\).

Giải:

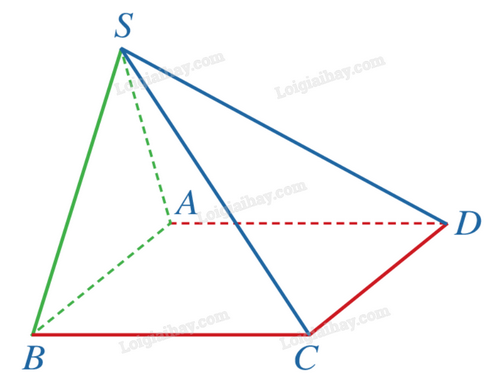
Do \((SAB) \bot (ABCD)\), \((SAB) \cap (ABCD) = AB\), \(BC \subset (ABCD)\) và \(BC \bot AB\) nên \(BC \bot (SAB)\).

Ta có \(BC \subset (SBC)\) và \(BC \bot (SAB)\), suy ra \((SBC) \bot (SAB)\).

b) Tính chất 2:

Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

Chứng minh:

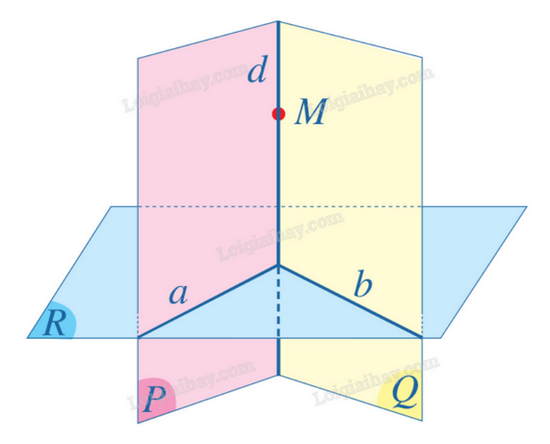
Giả sử hai mặt phẳng (P), (Q) cắt nhau theo giao tuyến d; (P) và (Q) cùng vuông góc với mặt phẳng (R). Gọi a, b lần lượt là giao tuyến của mặt phẳng (R) với hai mặt phẳng (P), (Q). Xét điểm M thuộc đường thẳng d.

Trong mặt phẳng (P), gọi \({d_1}\) là đường thẳng đi qua điểm M và vuông góc với đường thẳng a. Theo Tính chất 1, ta có: \({d_1} \bot (R)\).

Trong mặt phẳng (Q), gọi \({d_2}\) là đường thẳng đi qua điểm M và vuông góc với đường thẳng b. Theo Tính chất 1, ta có: \({d_2} \bot (R)\). Suy ra \({d_1}\) trùng \({d_2}\) nên hai đường thẳng đó cùng nằm trên cả hai mặt phẳng (P) và (Q). Cho nên \({d_1}\), \({d_2}\) và \(d\) trùng nhau. Vậy \(d \bot (R)\).

Ví dụ minh hoạ:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a với tâm O, \(SO = \frac{{a\sqrt 2 }}{2}\). Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD).

a) Chứng minh rằng \(SO \bot (ABCD)\).

b) Tính góc giữa đường thẳng SA và mặt phẳng (ABCD).

Giải:

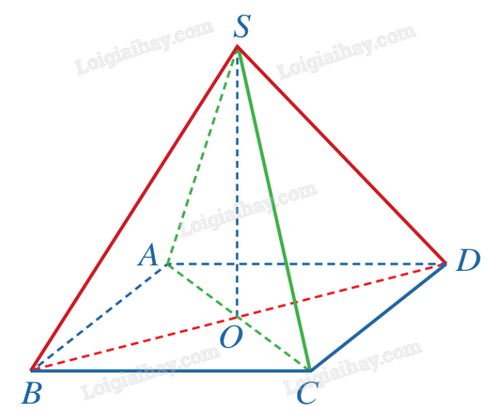
a) Ta có \((SAC) \bot (ABCD)\), \((SBD) \bot (ABCD)\) và \((SAC) \cap (SBD) = SO\). Theo Tính chất 2, ta có: \(SO \bot (ABCD)\).

b) Do \(SO \bot (ABCD)\) nên góc giữa SA và mặt phẳng (ABCD) là góc \(\widehat {SAO}\).

Vì tam giác SAO vuông tại O có \(SO = AO = \frac{{a\sqrt 2 }}{2}\) nên tam giác SAO vuông cân tại O.

Suy ra \(\widehat {SAO} = {45^o}\). Vậy góc giữa đường thẳng SA và mặt phẳng (ABCD) là \({45^o}\).