1. Số đo của góc nhị diện
Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.
Nếu số đo góc phẳng nhị diện bằng \({90^o}\) thì góc nhị diện đó gọi là góc nhị diện vuông.
Số đo của góc nhị diện từ \({0^o}\) đến \({180^o}\).
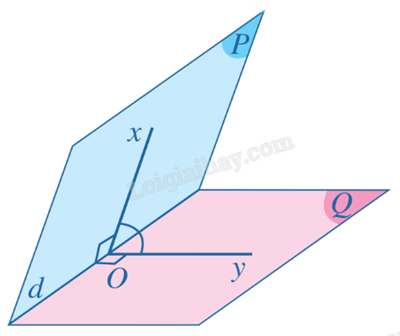
2. Cách tính số đo của góc nhị diện
Tính số đo của góc phẳng nhị diện.
Ví dụ minh hoạ:
1) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a, \(SA \bot (ABC)\), \(SA = a\sqrt 3 \). Tính số đo của mỗi góc nhị diện sau:
a) [B, SA, C];
b) [A, BC, S].
Giải:
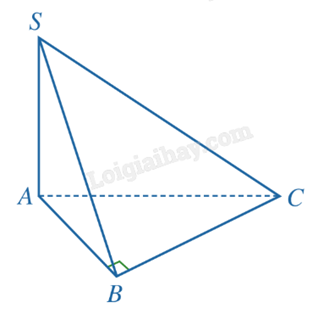
a) Vì \(SA \bot (ABC)\) nên \(SA \bot AB\), \(SA \bot AC\). Do đó, góc \(\widehat {BAC}\) là góc phẳng nhị diện của góc nhị diện [B, SA, C].
Do tam giác ABC vuông cân tại B nên \(\widehat {BAC} = {45^o}\). Vậy số đo của góc nhị diện [B, SA, C] bằng \({45^o}\).
b) Vì \(SA \bot (ABC)\) nên \(SA \bot BC\). Mà \(BC \bot AB\) nên \(BC \bot (SAB)\), suy ra \(BC \bot SB\). Do đó góc \(\widehat {SBA}\) là góc phẳng nhị diện của góc nhị diện [A, BC, S].
Trong tam giác vuông SAB, ta có:
\(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \). Suy ra \(\widehat {SBA} = {60^o}\).
Vậy số đo của góc nhị diện [A, BC, S] bằng \({60^o}\).
2) Cho hình chóp S.ABCD có \(SA \bot (ABCD)\), đáy ABCD là hình thoi có cạnh bằng a, AC = a, \(SA = \frac{1}{2}a\). Gọi O là giao điểm của hai đường chéo hình thoi ABCD và H là hình chiếu của O trên SC.
a) Tính số đo của các góc nhị diện [B, SA, D]; [S, BD, A]; [S, BD, C].
b) Chứng minh rằng BHD là một góc phẳng của góc nhị diện [B, SC, D].
Giải:
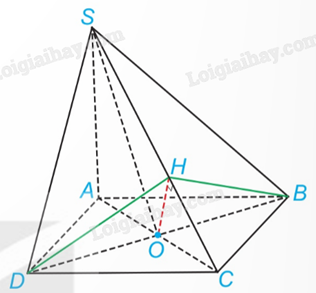
a) Vì \(SA \bot (ABCD)\) nên AB và AD vuông góc với SA. Vậy \(\widehat {BAD}\) là một góc phẳng của góc nhị diện [B, SA, D].
Hình thoi ABCD có cạnh bằng a và AC = a nên các tam giác ABC, ACD đều. Do đó \(BAD = {120^o}\). Vậy số đo của góc nhị diện [B, SA, D] bằng \({120^o}\).
Vì \(BD \bot AC\) và \(BD \bot SA\) nên \(BD \bot (SAC)\). Vậy AC và SO vuông góc với BD. Suy ra \(\widehat {AOS}\) là một góc phẳng của góc nhị diện [S, BD, A] và \(\widehat {COS}\) là một góc phẳng của góc nhị diện [S, BD, C].
Tam giác SAO vuông tại A và có \(SA = \frac{1}{2}a = AO\) nên \(\widehat {AOS} = {45^o}\). Suy ra \(\widehat {COS} = {180^o} - \widehat {AOS} = {135^o}\).
Vậy các góc nhị diện [S, BD, A], [S, BD, C] tương ứng có số đo là \({45^o}\), \({135^o}\).
b) Theo chứng minh trên, \(BD \bot (SAC)\) nên \(BD \bot SC\). Mặt khác, \(OH \bot SC\) nên \(SC \bot (BHD)\). Do đó, \(\widehat {BHD}\) là một góc phẳng của góc nhị diện [B, SC, D].

 Hai mặt phẳng vuông góc - Từ điển môn Toán 11
Hai mặt phẳng vuông góc - Từ điển môn Toán 11 






Danh sách bình luận