Định lí ba đường vuông góc là gì? - Toán 11

Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng d nằm trong mặt phẳng (P). Khi đó, d vuông góc với a khi và chỉ khi d vuông góc với hình chiếu a’ của a trên (P).

- Nếu a nằm trong (P) thì kết quả là hiển nhiên.

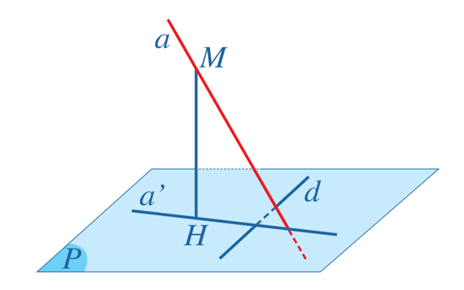
- Ta xét trường hợp a không nằm trong (P) (như hình vẽ).

Lấy điểm \(M \in a\). Gọi H là hình chiếu của M trên (P) thì a' đi qua H. Gọi (Q) là mặt phẳng chứa hai đường thẳng a và MH. Do \(MH \bot (P)\) mà \(d \subset (P)\) nên \(MH \bot d\).

Giả sử \(d \bot a'\). Khi đó, d vuông góc với hai đường thẳng cắt nhau trong mặt phẳng (Q) là a' và MH. Suy ra \(d \bot (Q)\), mà \(a \subset (Q)\) nên \(d \bot a\).

Giả sử \(d \bot a\). Khi đó, bằng cách chứng minh tương tự như trên, ta có: \(d \bot a'\).

Trong mặt phẳng (P) cho tam giác ABC vuông tại C. Trên đường thẳng vuông góc với mặt phẳng (P) tại A, ta lấy điểm S (S khác A).

a) Chứng minh rằng tam giác SBC vuông tại C.

b) Gọi AH là đường cao của tam giác SAC. Chứng minh rằng \(AH \bot (SBC)\).

Giải:

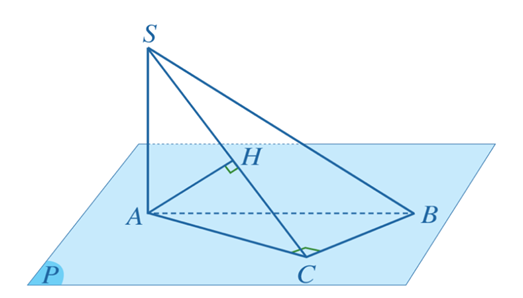
a) Vì \(SA \bot (ABC)\) nên AC là hình chiếu của SC trên mặt phẳng \((ABC)\). Mà \(BC \bot AC\) nên theo định lí ba đường vuông góc ta có \(BC \bot SC\). Vậy tam giác SBC vuông tại \(C\).

b) Ta có BC vuông góc với hai đường thẳng SA và AC cắt nhau trong mặt phẳng \((SAC)\) nên \(BC \bot (SAC)\), mà AH nằm trong mặt phẳng \((SAC)\) nên BC vuông góc với AH. Vì AH vuông góc với hai đường thẳng SC và BC cắt nhau trong mặt phẳng \((SBC)\) nên AH vuông góc với mặt phẳng \((SBC)\).