Cách xác định và tính góc giữa hai mặt phẳng - Toán 11

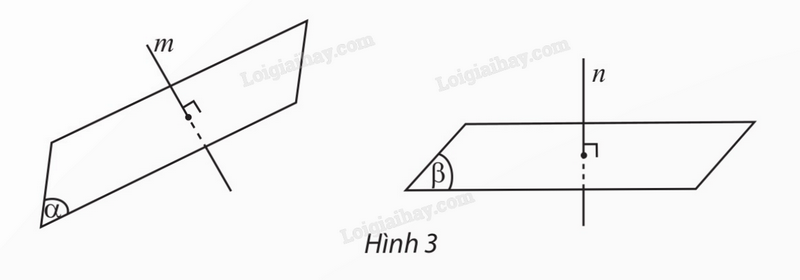
Góc giữa hai mặt phẳng \((\alpha )\) và \((\beta )\) là góc giữa hai đường thẳng lần lượt vuông góc với \((\alpha )\) và \((\beta )\), kí hiệu \(((\alpha ),(\beta ))\).

Ta có: \(((\alpha ),(\beta )) = (m,n)\) với \(m \bot (\alpha )\), \(n \bot (\beta )\).

Nhận xét: Nếu \(\varphi \) là góc giữa hai mặt phẳng (P) và (Q) thì \({0^\circ } < \varphi  < {90^\circ }\).

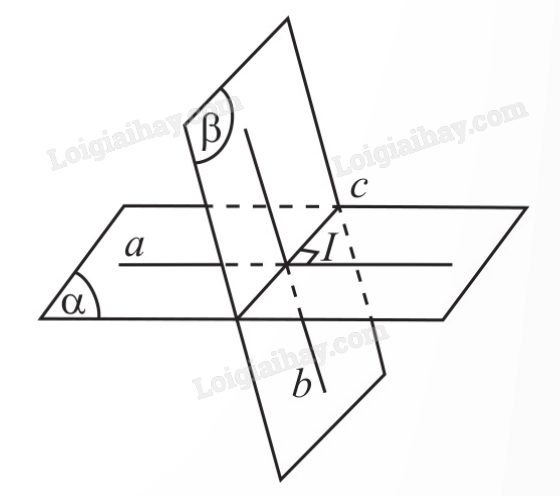
Người ta chứng minh được góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.

Cho \(c = (\alpha ) \cap (\beta )\):

\(((\alpha ),(\beta )) = (a,b)\) với \(a \subset (\alpha )\), \(b \subset (\beta )\), \(a \bot c\), \(b \bot c\).

Ví dụ minh hoạ:

1) Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bên SA vuông góc với mặt phẳng đáy. Tính góc giữa hai mặt phẳng:

a) (SAC) và (SAD);

b) (SAB) và (SAD).

Giải:

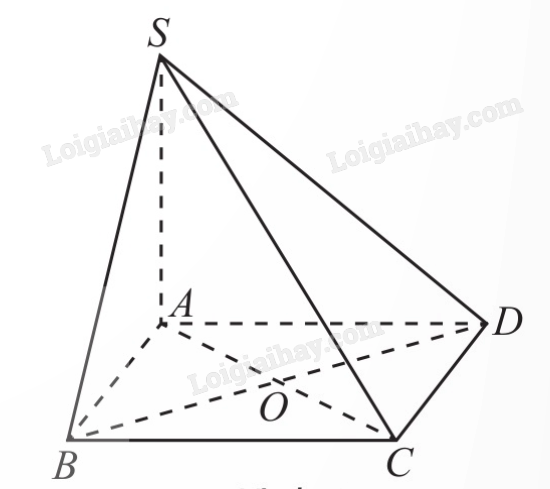
a) Ta có:

\(BO \bot SA\) và \(BO \bot AC\), suy ra \(BO \bot (SAC)\);

\(BA \bot SA\) và \(BA \bot AD\), suy ra \(BA \bot (SAD)\).

Do đó, nếu gọi góc giữa hai mặt phẳng (SAC) và (SAD) là \(\alpha \) thì \(\alpha  = (BO,BA) = \widehat {ABO} = {45^o}\).

b) Ta có:

\(CB \bot SA\) và \(CB \bot AB\), suy ra \(CB \bot (SAB)\);

\(CD \bot SA\) và \(CD \bot AD\), suy ra \(CD \bot (SAD)\).

Do đó, nếu gọi góc giữa hai mặt phẳng (SAB) và (SAD) là \(\beta \) thì \(\beta  = (CB,CD) = \widehat {BCD} = {90^o}\).