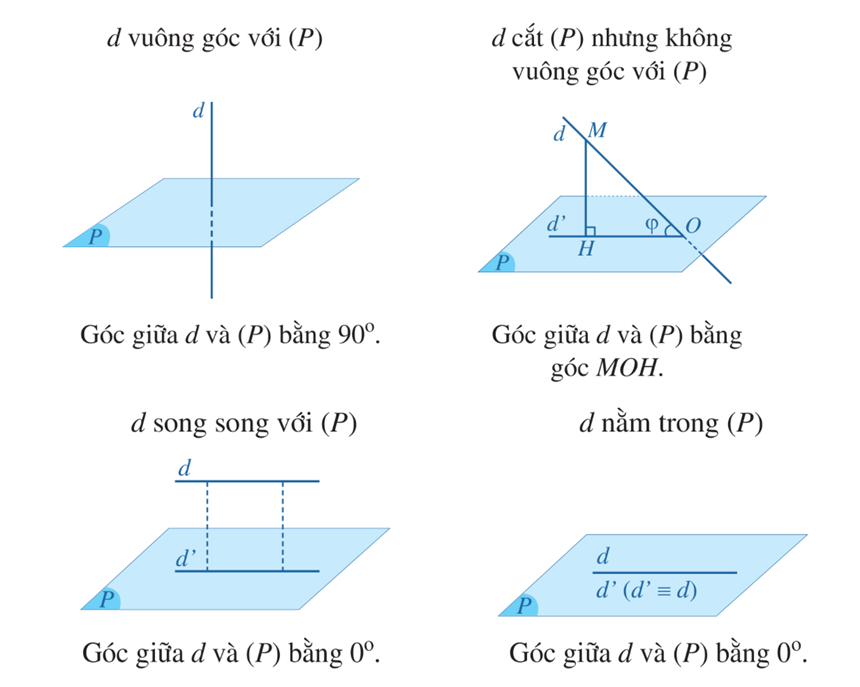
Cách tính góc giữa đường thẳng và mặt phẳng - Toán 11

Cho đường thẳng d và mặt phẳng (P), ta có định nghĩa:

- Nếu đường thẳng d vuông góc với mặt phẳng (P) thì góc giữa d và (P) bằng \({90^o}\).

- Nếu đường thẳng d không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng d và mặt phẳng (P) là góc giữa d và hình chiếu d’ của đường thẳng d trên (P).

Nhận xét: Góc giữa đường thẳng và mặt phẳng có số đo từ \({0^o}\) đến \({90^o}\).

Để tính góc giữa đường thẳng d và mặt phẳng (P), ta tính góc giữa đường thẳng d và hình chiếu d’ của d trên (P).

Ví dụ minh hoạ:

1) Cho hình chóp S.ABC có \(SA \bot (ABC)\).

a) Tính góc giữa đường thẳng SA và mặt phẳng (ABC).

b) Tính góc giữa đường thẳng SB và mặt phẳng (ABC), biết \(SA = \sqrt 3 AB\).

Giải:

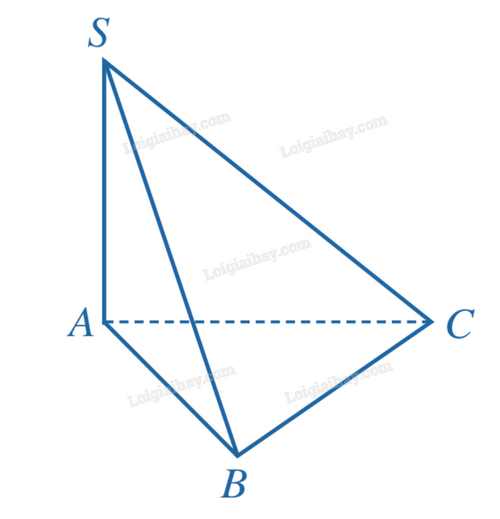
a) Vì \(SA \bot (ABC)\) nên góc giữa đường thẳng SA và mặt phẳng (ABC) bằng \({90^o}\).

b) Vì \(SA \bot (ABC)\) nên AB là hình chiếu của SB trên (ABC). Suy ra góc giữa đường thẳng SB và mặt phẳng (ABC) bằng \(\widehat {SBA}\).

Xét tam giác vuông SBA. Vì \(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \sqrt 3 \) nên \(\widehat {SBA} = {60^o}\).

Vậy góc giữa đường thẳng SB và mặt phẳng (ABC) bằng \({60^o}\).

2) Để ước lượng chiều cao của tháp khi không thể lên tới đỉnh tháp, người ta đo góc giữa tia nắng chiếu qua đỉnh tháp và mặt đất, đo chiều dài của bóng tháp trên mặt đất, từ đó ước lượng được chiều cao của tháp. Giả sử khi tia nắng tạo với mặt đất một góc \({40^o}\), chiều dài của bóng tháp là 114 m. Tính chiều cao của tháp theo đơn vị mét (làm tròn kết quả đến hàng phần mười).

Giải:

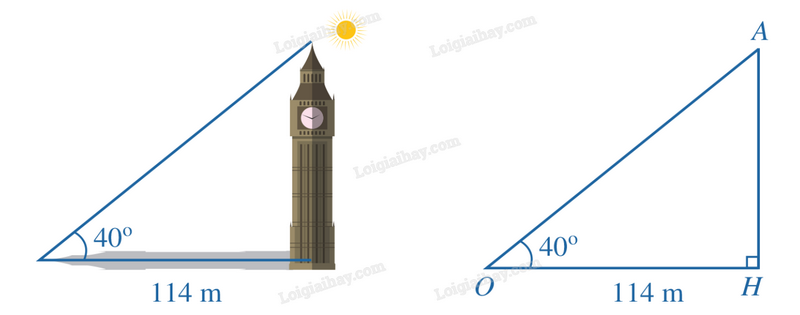
Đặt tên các điểm như hình.

Độ dài AH chỉ chiều cao của tháp, độ dài OH chỉ chiều dài của bóng tháp, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa tia nắng và mặt đất. Vì tam giác OAH vuông tại H nên:

\(AH = OH.\tan \widehat {AOH} = 114.\tan {40^o} \approx 95,7\) (m).