 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường th..
Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường th..
Lý thuyết về các góc tạo bởi một đường thẳng cắt hai đường thẳng
Nếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có một cặp góc so le trong bằng nhau thì...
1. Góc so le trong, góc đồng vị

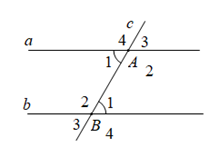
Trên hình vẽ ta có:
- Hai cặp góc so le trong:
\(\widehat{A_{1}}\) và \(\widehat{B_{3}}\); \(\widehat{A_{4}}\) và \(\widehat{B_{2}}\)
- Bốn cặp góc đồng vị:
\(\widehat{A_{1}}\) và \(\widehat{B_{1}}\); \(\widehat{A_{2}}\) và \(\widehat{B_{2}}\)
\(\widehat{A_{3}}\) và \(\widehat{B_{3}}\); \(\widehat{A_{4}}\) và \(\widehat{B_{4}}\).
2. Tính chất
Nếu đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b\), trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
a) Hai góc so le trong còn lại bằng nhau.
b) Hai góc đồng vị (trong mỗi cặp) bằng nhau.
c) Hai góc trong cùng phía bù nhau
Ví dụ: Đường thẳng c cắt hai đường thẳng song song a và b (như hình vẽ).
\({\widehat A_1} = {\widehat B_1} \Rightarrow \left\{ \begin{array}{l}{\widehat A_2} = {\widehat B_2}\\{\widehat A_3} = {\widehat B_1}\\{\widehat A_2} + {\widehat B_1} = {180^0}\end{array} \right.\)
Loigiaihay.com












Danh sách bình luận