Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường th..
Đề kiểm tra 15 phút - Đề số 2 - Bài 3, 4 - Chương 1 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 3, 4 - Chương 1 - Hình học 7
Đề bài
Xem hình vẽ biết \(\widehat {{A_4}} = {50^o}\) và \(\widehat {{B_2}} = {50^o}.\)
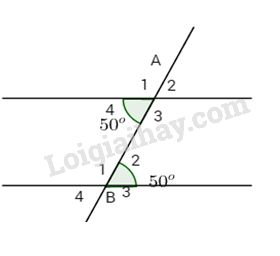
a) Hãy tính các góc còn lại.
b) Hãy so sánh số đo của hai góc so le trong bất kì, hai góc đồng vị bất kì.
c) Tính \(\widehat {{A_3}} + \widehat {{B_2}}\) và \(\widehat {{A_4}} + \widehat {{B_1}}\). Em có kết luận gì về tổng hai góc trong cùng phía?
Phương pháp giải - Xem chi tiết
Sử dụng:
Hai góc kề bù có tổng bằng \(180^0\)
Công thức cộng góc: Nếu tia Oz nằm giữa hai tia Ox và Oy thì \(\widehat {xOz} + \widehat {yOz} = \widehat {xOy}\)
Lời giải chi tiết
a) \(\widehat {{A_2}} = \widehat {{A_4}} = {50^o}\) (đối đỉnh); \(\widehat {{A_1}} + \widehat {{A_4}} = {180^o}\) (kề bù)
\(\widehat {{A_4}} + \widehat {{B_1}} = {50^o} + {130^o} = {180^o}.\) \( \Rightarrow \widehat {{A_1}} = {180^o} - \widehat {{A_4}} = {180^o} - {50^o} \)\(\,= {130^o};\)\(\,\widehat {{A_3}} = \widehat {{A_1}} = {130^o}\) (đối đỉnh).
Tương tự ta tính được \(\widehat {{B_4}} = {50^o};\,\widehat {{B_1}} = \widehat {{B_3}} = {130^o}.\)
b) Ta có \(\widehat {{A_4}} = \widehat {{B_2}} = {50^o};\,\widehat {{A_3}} = \widehat {{B_1}} = {130^o}.\) Các góc so le trong bằng nhau.
Ta có \(\widehat {{B_4}} = \widehat {{A_4}} = {50^o};\,\widehat {{B_1}} = \widehat {{A_1}} = {130^o};\)\(\,\widehat {{A_3}} = \widehat {{B_3}} = {130^o};\,\widehat {{A_2}} = \widehat {{B_2}} = {50^o}.\)
Các góc đồng vị bằng nhau.
c) \(\widehat {{A_3}} + \widehat {{B_2}} = {130^o} + {50^o} = {180^o};\)
\(\widehat {{A_4}} + \widehat {{B_1}} = {50^o} + {130^o} = {180^o}.\)
Tổng hai góc trong cùng phía bù nhau.
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 3 - Bài 3, 4 - Chương 1 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 3, 4 - Chương 1 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 5 - Bài 3, 4 - Chương 1 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 1 - Bài 3, 4 - Chương 1 - Hình học 7
- Bài 23 trang 89 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
