Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường th..
Đề kiểm tra 15 phút - Đề số 4 - Bài 3, 4 - Chương 1 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 3, 4 - Chương 1 - Hình học 7
Đề bài
Cho \(\widehat {xOy} = {40^o}\). Lấy A trên tia Ox. Vẽ tia At nằm trên nửa mặt phẳng bờ là đường thẳng Ox. Chứa tia Oy sao cho At cắt Oy tại B và \(\widehat {OAt} = {100^o}\). Gọi Am là tia phân giác của góc \(\widehat {xAt}\).
a) Chứng tỏ Am // Oy.
b) Trên nửa mặt phẳng không chứa điểm A bờ là đường thẳng Oy vẽ tia Bn. Hỏi để Bn song song với Ox thì số đo góc OBn phải bằng bao nhiêu?
Phương pháp giải - Xem chi tiết
Sử dụng:
Hai góc kề bù có tổng bằng \(180^0\)
Nếu đường thẳng \(c\) cắt hai đường thẳng \(a, b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau, hoặc cặp góc trong cùng phía bù nhau) thì \(a\) và \(b\) song song với nhau.
Lời giải chi tiết
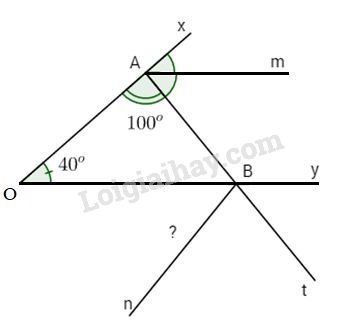
a) Ta có \(\widehat {xAt} + \widehat {OAt} = {180^o}\)(kề bù)
\(\eqalign{ & \Rightarrow \widehat {xAt} = {180^o} - \widehat {OAt} \cr & \,\,\,\,\, \Rightarrow \widehat {xAt} = {180^o} - {100^o} \cr} \)
\( \Rightarrow \widehat {xAt} = {80^o}\)
Am là tia phân giác của \(\widehat {xAt}\) nên
\(\widehat {xAm} = \widehat {tAm} = \dfrac{{\widehat {xAt}}}{ 2} = \dfrac{{{{80}^o}} }{ 2} = {40^0}.\)
Hai góc \(\widehat {xAm}\) và \(\widehat {xOy}\) ở vị trí đồng vị và \(\widehat {xAm} = \widehat {xOy} = {40^o}\). Do đó Am // Oy.
b) Hai góc \(\widehat {OBn}\) và \(\widehat {xOy}\) ở vị trí so le trong để Bn // Ox thì \(\widehat {OBn} = \widehat {xOy} = {40^o}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 5 - Bài 3, 4 - Chương 1 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 3, 4 - Chương 1 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 3, 4 - Chương 1 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 1 - Bài 3, 4 - Chương 1 - Hình học 7
- Bài 23 trang 89 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
