Bài 3. Phương trình mặt cầu - Toán 12 Chân trời sáng tạo

Lý thuyết Phương trình mặt cầu Toán 12 Chân trời sáng tạo

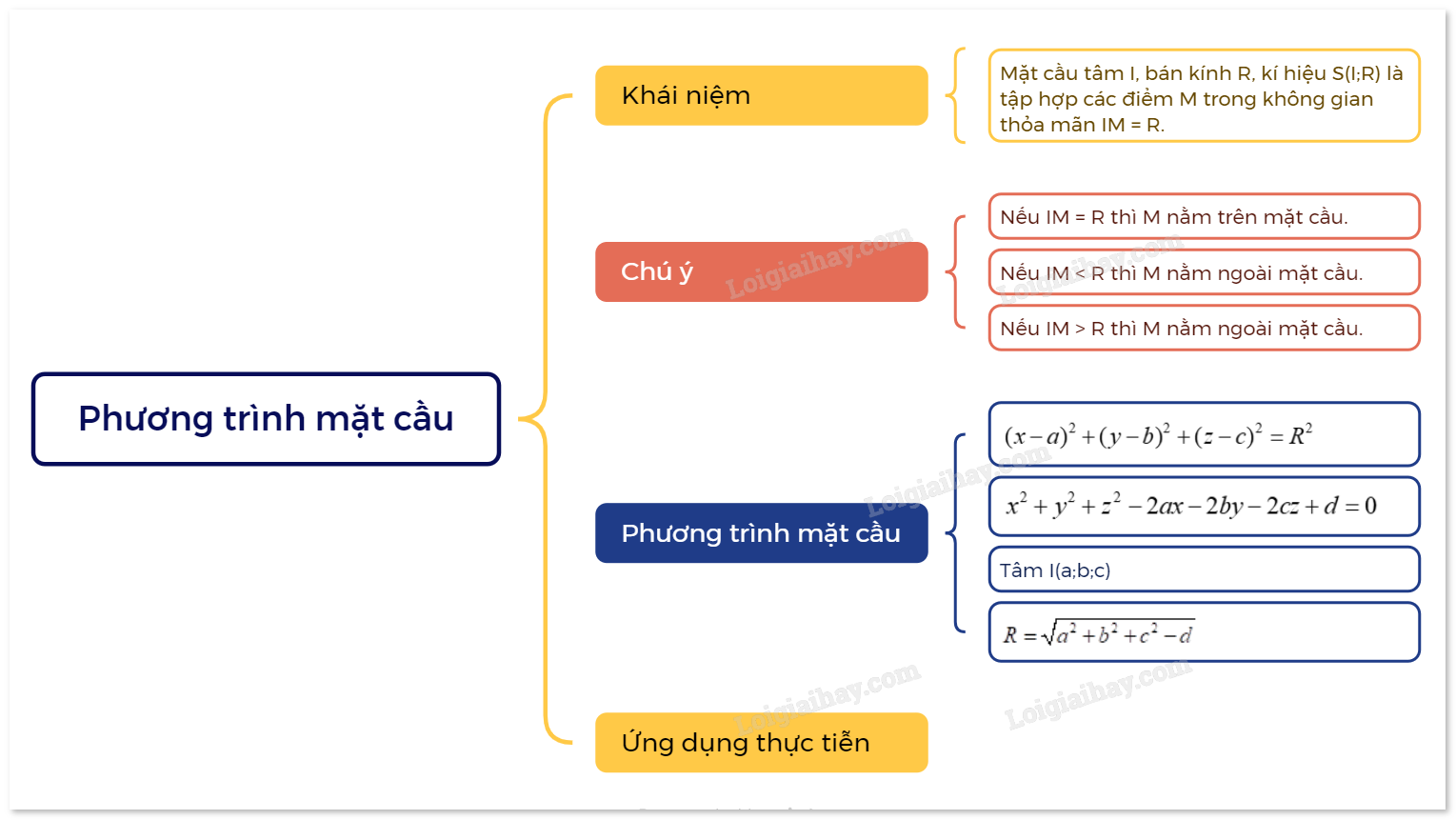
1. Phương trình mặt cầu trong không gian Khái niệm mặt cầu Trong không gian, cho điểm I và số dương R. Mặt cầu tâm I, bán kính R, kí hiệu S(I;R) là tập hợp các điểm M trong không gian thỏa mãn IM = R. Đoạn thẳng nối hai điểm thuộc mặt cầu và đi qua tâm I là đường kính mặt cầu.

1. Phương trình mặt cầu trong không gian

Khái niệm mặt cầu

Trong không gian, cho điểm I và số dương R. Mặt cầu tâm I, bán kính R, kí hiệu S(I;R) là tập hợp các điểm M trong không gian thỏa mãn IM = R. Đoạn thẳng nối hai điểm thuộc mặt cầu và đi qua tâm I là đường kính mặt cầu.

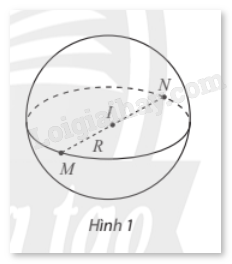
Chú ý: Cho mặt cầu S(I;R).

Nếu IM = R thì M nằm trên mặt cầu.

Nếu IM < R thì M nằm ngoài mặt cầu.

Nếu IM > R thì M nằm ngoài mặt cầu.

Phương trình mặt cầu

Trong không gian Oxyz, mặt cầu (S) tâm I(a;b;c) bán kính R có phương trình

(x - a)^{2} + (y - b)^{2} + (z - c)^{2} = R^{2}

${(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}$

Nhận xét: Phương trình ${x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0$ với ${a^2} + {b^2} + {c^2} - d > 0$ là phương trình của mặt cầu tâm I(a;b;c) và bán kính $R = \sqrt {{a^2} + {b^2} + {c^2} - d}$ .

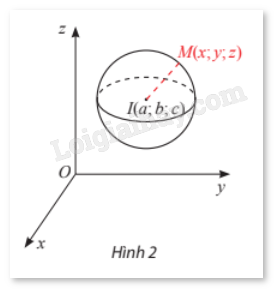
Ví dụ 1: Viết phương trình mặt cầu (S):

a) Có tâm I(1;2;3), bán kính R = 5.

b) Có đường kính AB với A(1;3;7) và B(3;5;1).

c) Có tâm A(1;0;2) và đi qua điểm B(2;4;1).

Giải:

a) Mặt cầu (S) có phương trình ${(x - 1)^2} + {(y - 2)^2} + {(z - 3)^3} = 25$ .

b) Mặt cầu (S) có đường kính AB nên có tâm J(2;4;4) là trung điểm AB và bán kính R = JA = $\sqrt {11}$ .

Vậy (S) có phương trình ${(x - 2)^2} + {(y - 4)^2} + {(z - 4)^2} = 11$ .

c) Mặt cầu (S) có tâm A(1;0;-2) và đi qua điểm B(2;4;1) nên có bán kính R = AB = $\sqrt {26}$ .

Vậy (S) có phương trình ${(x - 1)^2} + {y^2} + {(z + 2)^2} = 26$ .

Ví dụ 2: Xác định tâm và bán kính mặt cầu có phương trình:

a) (S): ${(x - 3)^2} + {(y - 7)^2} + {(z + 1)^2} = 81$ .

b) (S’): ${x^2} + {y^2} + {z^2} = 4$ .

Giải:

a) Mặt cầu (S) có tâm I(3;7;-1) và bán kính R = $\sqrt {81}$ = 9.

b) Mặt cầu (S’) có tâm O(0;0;0) và bán kính R’ = $\sqrt 4$ = 2.

Ví dụ 3: Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính mặt cầu đó.

a) ${x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0$ .

b) ${x^2} + {y^2} + {z^2} + x + y - 6z + 33 = 0$ .

Giải:

a) Phương trình ${x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0$ có dạng ${x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0$ với $a = - 4;b = 3;c = - 1;d = - 10$ .

Ta có ${a^2} + {b^2} + {c^2} - d = 16 + 9 + 1 + 10 = 36 > 0$ .

Suy ra phương trình đã cho là phương trình mặt cầu tâm I(-4;3;-1), bán kính R = 6.

b) Phương trình ${x^2} + {y^2} + {z^2} + x + y - 6z + 33 = 0$ có dạng ${x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0$ với $a = - \frac{1}{2};b = - \frac{1}{2};c = 3;d = 33$ .

Ta có ${a^2} + {b^2} + {c^2} - d = \frac{1}{4} + \frac{1}{4} + 9 - 33 = - \frac{{47}}{2} < 0$ .

Suy ra phương trình đã cho không phải phương trình mặt cầu.

2. Vận dụng của phương trình mặt cầu

Ví dụ: Công nghệ hỗ trợ trọng tài VAR (Video Assisstant Referee) thiết lập một hệ tọa độ Oxyz để theo dõi vị trí của quả bóng M. Cho biết M đang nằm trên mặt sân có phương trình z = 0, đồng thời thuộc mặt cầu (S): ${(x - 32)^2} + {(y - 50)^2} + {(z - 10)^2} = 109$ (đơn vị độ dài tính theo mét).

a) Tìm tọa độ tâm I và bán kính R của mặt cầu (S).

b) Tìm tọa độ hình chiếu vuông góc J của tâm I trên mặt sân.

c) Tính khoảng cách từ vị trí M của quả bóng đến điểm J.

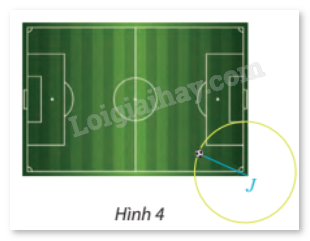
Giải:

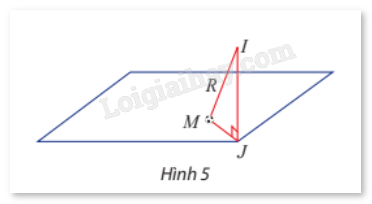
Mặt cầu (S) có phương trình ${(x - 32)^2} + {(y - 50)^2} + {(z - 10)^2} = 109$ nên có tâm I(32;50;0) và bán kính $R = \sqrt {109}$ .

b) Trong không gian Oxyz, mặt sân có phương trình z = 0 trùng với mặt phẳng tọa độ (Oxy), suy ra hình chiếu vuông góc của điểm I(32;50;10) xuống mặt sân có tọa độ J(32;50;0).

c) Trong tam giác vuông IJM, ta có IJ = 10, IM = R, suy ra

$JM = \sqrt {I{M^2} - I{J^2}} = \sqrt {109 - 100} = 3$ .

Vậy khoảng cách từ vị trí M của quả bóng đến điểm J là 3m.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 61, 62, 63 SGK Toán 12 tập 2 - Chân trời sáng tạo
Trong không gian (Oxyz), cho mặt cầu (Sleft( {I;R} right)) có tâm (Ileft( {a;b;c} right)) và bán kính (R). Xét một điểm (Mleft( {x;y;z} right)) thay đổi. a) Tính khoảng cách (IM) theo (x), (y), (z) và (a), (b), (c). b) Nêu điều kiện cần và đủ của (x), (y), (z) để điểm (Mleft( {x;y;z} right)) nằm trên mặt cầu (Sleft( {I;R} right)).
Giải mục 2 trang 63, 64 SGK Toán 12 tập 2 - Chân trời sáng tạo
Bề mặt của một bóng thám không dạng hình cầu có phương trình ({x^2} + {y^2} + {z^2} - 200x - 600y - {rm{4 000}}z + {rm{4 099 900}} = 0). Tìm toạ độ tâm và bán kính mặt cầu.
Giải bài tập 1 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Viết phương trình mặt cầu (left( S right)): a) Có tâm (Ileft( {7; - 3;0} right)), bán kính (R = 8). b) Có tâm (Mleft( {3;1; - 4} right)) và đi qua điểm (Nleft( {1;0;1} right)). c) Có đường kính (AB) với (Aleft( {4;6;8} right)) và (Bleft( {2;4;4} right)).
Giải bài tập 2 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó. a) ({x^2} + {y^2} + {z^2} + 5x - 7y + z - 1 = 0). b) ({x^2} + {y^2} + {z^2} + 4x + 6y - 2z + 100 = 0). c) ({x^2} + {y^2} + {z^2} - x - y - z + frac{1}{2} = 0).
Giải bài tập 3 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Cho hai điểm (Aleft( {1;0;0} right)) và (Bleft( {5;0;0} right)). Chứng minh rằng nếu điểm (Mleft( {x;y;z} right)) thoả mãn (overrightarrow {MA} .overrightarrow {MB} = 0) thì (M) thuộc một mặt cầu (left( S right)). Tìm tâm và bán kính của (left( S right)).
Giải bài tập 4 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Phần mềm mô phỏng thiết bị thám hiẻm đại dương có dạng hình cầu trong không gian (Oxyz). Cho biết toạ độ tâm mặt cầu là (Ileft( {360;200;400} right)) và bán kính (r = 2{rm{ m}}). Viết phương trình mặt cầu.
Giải bài tập 5 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Người ta muốn thiết kế một bồn chứa khí hoá lỏng hình cầu bằng phần mềm 3D. Cho biết phương trình bề mặt của bồn chứa là (left( S right):{left( {x - 6} right)^2} + {left( {y - 6} right)^2} + {left( {z - 6} right)^2} = 25). Phương trình mặt phẳng chứa nắp là (left( P right):z = 10). a) Tìm tâm và bán kính của bồn chứa. b) Tính khoảng cách từ tâm bồn chứa đến mặt phẳng của nắp.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.