Lý thuyết Đường tiệm cận của đồ thị hàm số Toán 12 Kết nối tri thức

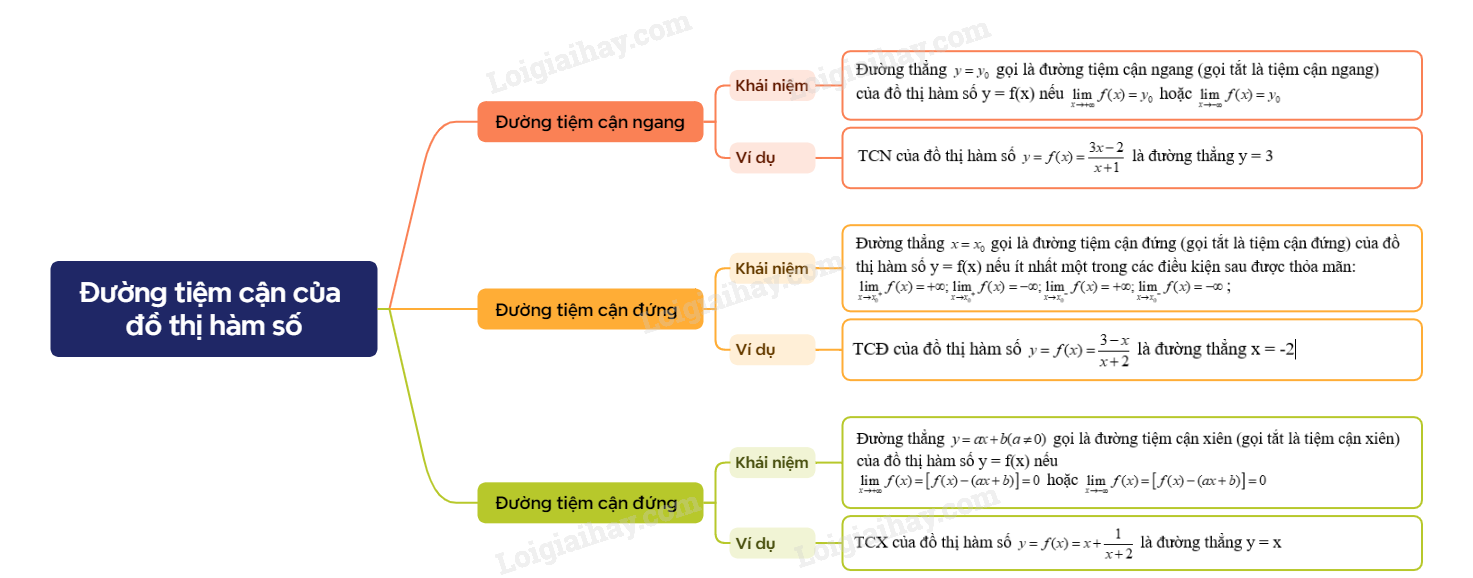
1. Đường tiệm cận ngang

1. Đường tiệm cận ngang

Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\)

Ví dụ: Tìm TCN của đồ thị hàm số \(y = f(x) = \frac{{3x - 2}}{{x + 1}}\)

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\)

Vậy đồ thị hàm số f(x) có TCN là y = 3.

2. Đường tiệm cận đứng

Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \);

Ví dụ: Tìm TCĐ của đồ thị hàm số \(y = f(x) = \frac{{3 - x}}{{x + 2}}\)

Ta có: \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{3 - x}}{{x + 2}} = + \infty \)

Vậy đồ thị hàm số có TCĐ là x = -2

3.Đường tiệm cận xiên

Đường thẳng \(y = ax + b(a \ne 0)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu

\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\)

Ví dụ: Tìm TCX của đồ thị hàm số \(y = f(x) = x + \frac{1}{{x + 2}}\)

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 2}} = 0\)

Vậy đồ thị hàm số có TCX là y = x

Bình luận

Chia sẻ

Bình chọn:

4 trên 5 phiếu

Bài tiếp theo

Giải mục 1 trang 20, 21 SGK Toán 12 tập 1 - Kết nối tri thức
Đường tiệm cận ngang
Giải mục 2 trang 21, 22 SGK Toán 12 tập 1 - Kết nối tri thức
Đường tiệm cận đứng
Giải mục 3 trang 23, 24 SGK Toán 12 tập 1 - Kết nối tri thức
Đường tiệm cận xiên
Giải bài tập 1.16 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Hình 1.26 là đồ thị của hàm số (y = fleft( x right) = frac{{2{x^2}}}{{{x^2} - 1}}) Sử dụng đồ thị này, hãy: a) Viết kết quả của các giới hạn sau: (mathop {lim }limits_{x to - infty } fleft( x right)); (mathop {lim }limits_{x to + infty } fleft( x right)); (mathop {lim }limits_{x to {1^ - }} fleft( x right)); (mathop {lim }limits_{x to - {1^ + }} fleft( x right)) b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.
Giải bài tập 1.17 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Đường thẳng \(x = 1\) có phải là tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 3}}{{x - 1}}\) không?
Giải bài tập 1.18 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm các tiệm cận của đồ thị hàm số sau: a) \(y = \frac{{3 - x}}{{2x + 1}}\); b) \(y = \frac{{2{x^2} + x - 1}}{{x + 2}}\).
Giải bài tập 1.19 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là \(C\left( x \right) = 2x + 50\) (triệu đồng). Khi đó, \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Tính chất này nói lên điều gì?
Giải bài tập 1.20 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Một mảnh vườn hình chữ nhật có diện tích bằng \(144{m^2}\). Biết độ dài một cạnh của mảnh vườn là x (m). a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn. b) Tìm các tiệm cận của đồ thị hàm số P(x).