Hàm số đồng biến, nghịch biến là gì? Cách xét tính đơn điệu của hàm số - Toán 12

Giả sử hàm số \(y = f(x)\) xác định trên \(K\).

Hàm số \(y = f(x)\) gọi là đồng biến (tăng) trên \(K\) nếu với mọi \({x_1}\), \({x_2}\) thuộc \(K\) mà \({x_1} < {x_2}\) thì \(f({x_1}) < f({x_2})\).

Hàm số \(y = f(x)\) gọi là nghịch biến (giảm) trên \(K\) nếu với mọi \({x_1}\), \({x_2}\) thuộc \(K\) mà \({x_1} < {x_2}\) thì \(f({x_1}) > f({x_2})\).

Hàm số đồng biến hoặc nghịch biến trên \(K\) được gọi chung là đơn điệu trên \(K\).

Cho hàm số \(y = f(x)\) xác định trên tập \(K \subset \mathbb{R}\), với \(K\) là một khoảng, nửa khoảng hoặc đoạn. Quan sát hình dạng đồ thị \(y = f(x)\) trên \(K\).

- Nếu đồ thị đi lên từ trái sang phải thì hàm số \(y = f(x)\) đồng biến trên \(K\).

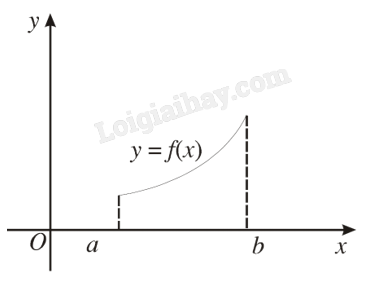
- Nếu đồ thị đi xuống từ trái sang phải thì hàm số \(y = f(x)\) nghịch biến trên \(K\).

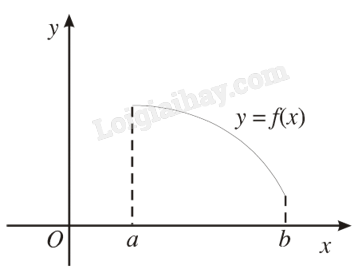
Ví dụ minh hoạ:

Câu 1. Xét sự biến thiên của hàm số y = f(x) trên khoảng (-2;9) có đồ thị như hình vẽ.

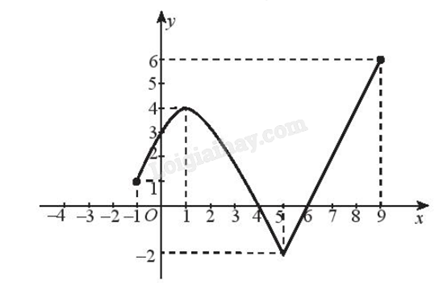
Giải:

Hàm số đồng biến trên (-1;1) vì đồ thị đi lên từ trái sang phải.

Hàm số nghịch biến trên (1;5) vì đồ thị đi xuống từ trái sang phải.

Hàm số đồng biến trên (5;9) vì đồ thị đi lên từ trái sang phải.

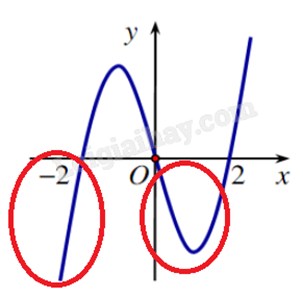
Câu 2. Cho hàm số y = f(x) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

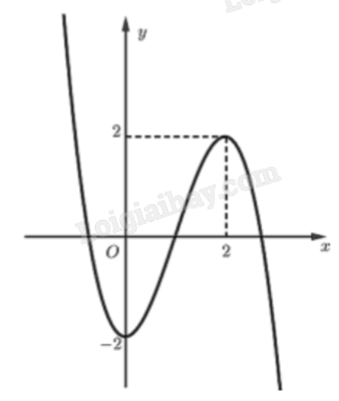
A. \(\left( { - \infty ;2} \right)\)

B. \(\left( {0;2} \right)\)

C. \(\left( { - 2;2} \right)\)

D. \(\left( {2; + \infty } \right)\)

Giải:

Đồ thị hàm số y = f(x) đi lên từ trái sang phải trên khoảng (0;2) nên hàm số đồng biến trên (0;2).

Đáp án B.

Câu 3. Cho hàm số y = f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình vẽ bên. Mệnh đề nào sau đây đúng?

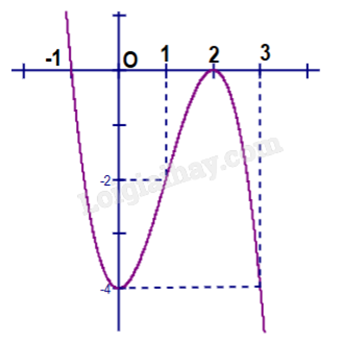
A. Hàm số đồng biến trên khoảng (-1;1)

B. Hàm số đồng biến trên khoảng (-4;2)

C. Hàm số nghịch biến trên khoảng (-1;0) và (2;3)

D. Hàm số nghịch biến trên khoảng (-4;1)

Giải:

Hàm số nghịch biến trên khoảng (-1;0) và (2;3) vì đồ thị hàm số đi xuống từ trái sang phải trên hai khoảng đó.

Đáp án C.

Cho hàm số \(y = f(x)\) xác định trên tập \(K \subset \mathbb{R}\), với \(K\) là một \(K\)hoảng, nửa \(K\)hoảng hoặc đoạn. Quan sát bảng biến thiên hoặc bảng xét dấu đồ thị \(y = f(x)\) trên \(K\).

Cách 1:

- Nếu hướng đồ thị (mũi tên) đi lên từ trái sang phải thì hàm số \(y = f(x)\) đồng biến trên \(K\).

- Nếu hướng đồ thị (mũi tên) đi xuống từ trái sang phải thì hàm số \(y = f(x)\) nghịch biến trên \(K\).

Cách 2:

- Nếu f’(x) dương thì hàm số \(y = f(x)\) đồng biến trên \(K\).

- Nếu f’(x) âm thì hàm số \(y = f(x)\) nghịch biến trên \(K\).

Ví dụ minh hoạ:

Xét sự biến thiên của hàm số \(y = f(x)\) có bảng biến thiên của như sau:

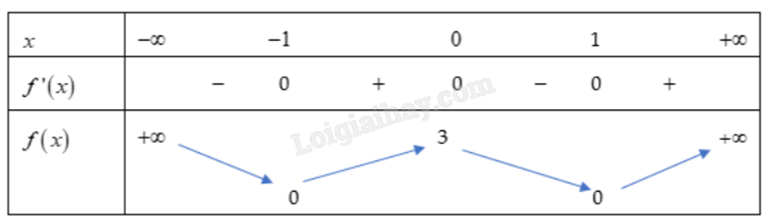
Giải:

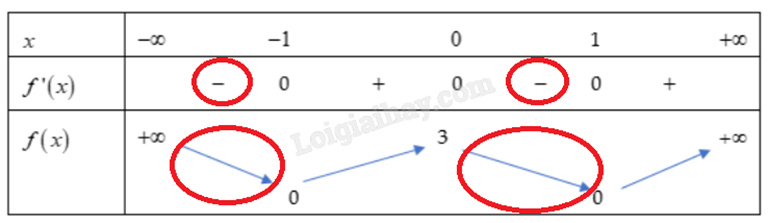
Hàm số đồng biến trên các khoảng (-1;0) và \((1; + \infty )\).

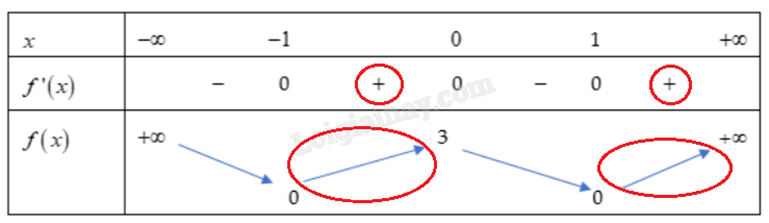
Hàm số nghịch biến trên các khoảng \(( - \infty ; - 1)\) và (0;1).

Cho hàm số \(y = f(x)\) xác định trên tập \(K \subset \mathbb{R}\), với \(K\) là một khoảng, nửa khoảng hoặc đoạn.

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính đạo hàm y’ = \(f’(x)\).

Bước 3: Lập bảng biến thiên của hàm số \(y = f(x)\).

Bước 4: Dựa vào bảng biến thiên, kết luận:

- Nếu hướng đồ thị (mũi tên) đi lên từ trái sang phải, hoặc \(f’(x)\) dương thì hàm số \(y = f(x)\) đồng biến trên \(K\).

- Nếu hướng đồ thị (mũi tên) đi xuống từ trái sang phải, hoặc \(f’(x)\) âm thì hàm số \(y = f(x)\) nghịch biến trên \(K\).

Ví dụ minh hoạ:

Xét sự biến thiên của các hàm số sau:

a) \(y = - {x^3} + 3x - 6\).

b) \(y = \frac{{x - 1}}{{x + 2}}\).

c) \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\).

d) \(y = \frac{{3x}}{{{x^2} - 9}}\).

Giải:

a) \(y =  - {x^3} + 3x - 6\).

Hàm số xác định trên R.

Ta có: \(y' =  - 3{x^2} + 3\).

Xét \(y' = 0 \Rightarrow  - 3{x^2} + 3 = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x =  - 1}\end{array}} \right.\).

Từ đó ta có bảng biến thiên là:

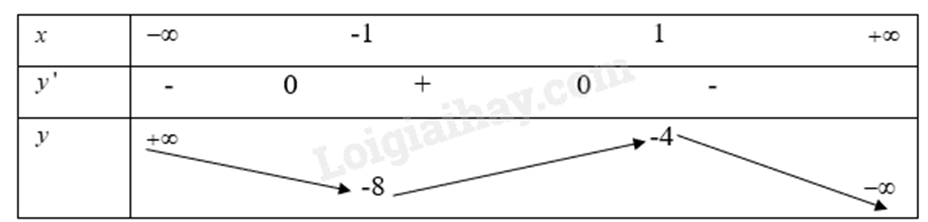
Từ bảng biến thiên ta có:

Hàm số \(y =  - {x^3} + 3x - 6\) đồng biến trên khoảng \(( - 1;1)\).

Hàm số \(y =  - {x^3} + 3x - 6\) nghịch biến trên khoảng \(( - \infty ; - 1)\), \((1; + \infty )\).

b) \(y = \frac{{x - 1}}{{x + 2}}\)

Hàm số trên xác định trên R\{2}.

Ta có: \(y' = \frac{3}{{{{(x + 2)}^2}}}\).

Vì \(y' = \frac{3}{{{{(x + 2)}^2}}} > 0\) với \(\forall x \in R\backslash \{ {\rm{\;}} - 2\} \).

Nên hàm số \(y = \frac{{x - 1}}{{x + 2}}\) đồng biến trên khoảng \(( - \infty ;2)\), \((2; + \infty )\).

c) \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\).

Hàm số xác định trên R\{-1}.

Ta có: \(y' = \frac{{( - 2x + 2)(x + 1) - ( - {x^2} + 2x + 2)}}{{{{(x + 1)}^2}}} = \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}\).

Xét \(y' = 0 \Rightarrow  - {x^2} - 2x = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x =  - 2}\end{array}} \right.\).

Từ đó ta có bảng biến thiên là:

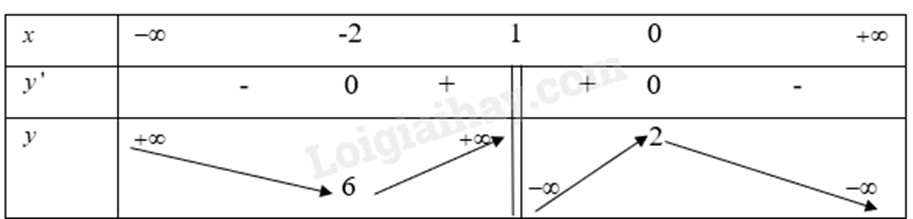
Từ bảng biến thiên, ta có:

Hàm số \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\) đồng biến trên khoảng \(( - 2;1)\), \((1;2)\).

Hàm số \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\) nghịch biến trên khoảng \(( - \infty ; - 2)\), \((0; + \infty )\).

d) \(y = \frac{{3x}}{{{x^2} - 9}}\).

Hàm số trên xác định trên R\{-3;3}.

Ta có: \(y' = \frac{{3({x^2} - 9) - 3x.2x}}{{{{({x^2} - 9)}^2}}}\) \( = \frac{{ - 3{x^2} - 27}}{{{{({x^2} - 9)}^2}}}\).

Vì \(y' = \frac{{ - 3{x^2} - 27}}{{{{({x^2} - 9)}^2}}} < 0\) với \(\forall x \in R\backslash \{  - 3;3\} \).

Vậy hàm số \(y = \frac{{3x}}{{{x^2} - 9}}\) nghịch biến trên khoảng \(( - \infty ; - 3)\), \(( - 3;3)\), \((3; + \infty )\).

Cho hàm số \(y = f(x)\) và đồ thị y = \(f’(x)\). Trên tập xác định của hàm số:

- Hàm số \(y = f(x)\) đồng biến trên khoảng \(f’(x)\) > 0, hay phần đồ thị y = \(f’(x)\) nằm phía trên trục hoành.

- Hàm số \(y = f(x)\) đồng nghịch trên khoảng \(f’(x)\) < 0, hay phần đồ thị y = \(f’(x)\) nằm phía dưới trục hoành.

Ví dụ minh hoạ:

Cho hàm số f(x) xác định trên \(\mathbb{R}\) và có đồ thị hàm số \(f’(x)\) là đường cong dưới đây. Xét sự biến thiên của hàm số f(x).

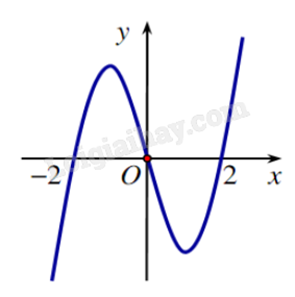
Giải:

Hàm số đồng biến trên khoảng \(( - 2;0)\) và \((2; + \infty )\) do phần đồ thị nằm phía trên trục hoành.

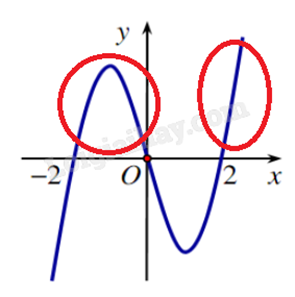
Hàm số nghịch biến trên khoảng \(( - \infty ; - 2)\) và \((0;2)\) do phần đồ thị nằm phía dưới trục hoành.

Cho hàm số \(y = f(x)\) liên tục trên \(K\).

Bước 1: Lập bảng xét dấu của \(f’(x)\).

Bước 2: Kết luận:

- Nếu \(f’(x)\) dương thì hàm số \(y = f(x)\) đồng biến trên \(K\).

- Nếu \(f’(x)\) âm thì hàm số \(y = f(x)\) nghịch biến trên \(K\).

Ví dụ minh hoạ:

Xét sự biến thiên của của hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có \(f'(x) = {(x + 1)^2}{(x - 1)^3}(2 - x)\).

Giải:

\(f'(x) = {(x + 1)^2}{(x - 1)^3}(2 - x) = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 1\\x = 2\end{array} \right.\).

Lập bảng xét dấu như sau:

- Điền các nghiệm của phương trình \(f’(x)\) = 0 vừa tìm theo thứ tự từ nhỏ đến lớn (hàng 1).

- Tương ứng với các nghiệm x đó, giá trị của \(f’(x)\) = 0 (hàng 2).

- Cần điền dấu vào các khoảng trống để được bảng xét dấu hoàn thiện.

Xét khoảng \(( - \infty ; - 1)\): Lấy giá trị x bất kì trong khoảng \(( - \infty ; - 1)\) thay vào \(f’(x)\), giả sử x = -2:

\(f'( - 2) = {( - 2 + 1)^2}{( - 2 - 1)^3}(2 + 2) =  - 108 < 0\). Vậy ta điền dấu “-”.

Làm tương tự với các khoảng còn lại, ta được bảng xét dấu hoàn thiện:

Vậy hàm số \(y = f(x)\) đồng biến trên khoảng (1;2), nghịch biến trên khoảng \(( - \infty ; - 1)\), (-1;1) và \((2; + \infty )\).