Cách tìm m để hàm số đồng biến, nghịch biến ứng dụng đạo hàm - Toán 12

Giả sử hàm số \(y = f(x)\) xác định trên \(K\).

Hàm số \(y = f(x)\) gọi là đồng biến (tăng) trên \(K\) nếu với mọi \({x_1}\), \({x_2}\) thuộc \(K\) mà \({x_1} < {x_2}\) thì \(f({x_1}) < f({x_2})\).

Hàm số \(y = f(x)\) gọi là nghịch biến (giảm) trên \(K\) nếu với mọi \({x_1}\), \({x_2}\) thuộc \(K\) mà \({x_1} < {x_2}\) thì \(f({x_1}) > f({x_2})\).

Hàm số đồng biến hoặc nghịch biến trên \(K\) được gọi chung là đơn điệu trên \(K\).

Cho hàm số y = f(x).

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính đạo hàm y’ = f’(x).

Bước 3:

- Đề bài yêu cầu hàm số đồng biến thì tìm điều kiện để:

+ \(f'(x) \ge m\) với hàm đa thức.

+ \(f'(x) > m\) với hàm phân thức bậc nhất.

- Đề bài yêu cầu hàm số nghịch biến thì tìm điều kiện để:

+ \(f'(x) \le m\) với hàm đa thức.

+ \(f'(x) < m\) với hàm phân thức bậc nhất.

Dấu “=” xảy ra tại hữu hạn điểm.

Ví dụ minh hoạ:

a) Tìm tất cả các giá trị của m để hàm số \(y = {x^3} + (m + 1){x^2} + 3x + 2025\) đồng biến trên \(\mathbb{R}\).

b) Tìm tất cả các giá trị m để hàm số \(y = \frac{{{m^2} - 4m}}{{{{(x + m)}^2}}}\) nghịch biến trên các khoảng xác định.

Giải:

a) \(y = {x^3} + (m + 1){x^2} + 3x + 2025\).

TXĐ: \(D = \mathbb{R}\).

Ta có \(y' = 3{x^2} + 2(m + 1)x + 3\).

Hàm số \(y = {x^3} + (m + 1){x^2} + 3x + 2025\) đồng biến trên \(\mathbb{R}\) khi và chỉ khi \(y' \ge 0\), \(\forall x \in \mathbb{R}\).

Khi đó \(3{x^2} + 2(m + 1)x + 3 \ge 0 \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {(m + 1)^2} - 9 \le 0\\a = 3 > 0\end{array} \right. \Leftrightarrow {m^2} + 2m - 8 \le 0 \Leftrightarrow  - 4 \le m \le 2\).

b) \(y = \frac{{mx + 4m}}{{x + m}}\).

TXĐ: \(D = \mathbb{R}\backslash \{  - m\} \).

Ta có \(y' = \frac{{{m^2} - 4m}}{{{{(x + m)}^2}}}\).

Hàm số \(y = \frac{{mx + 4m}}{{x + m}}\) nghịch biến trên khoảng xác định khi và chỉ khi:

\(y' = \frac{{{m^2} - 4m}}{{{{(x + m)}^2}}} < 0 \Leftrightarrow {m^2} - 4m < 0 \Leftrightarrow 0 < m < 4\).

1) Đối với hàm đa thức:

Bước 1: Tính đạo hàm f’(x).

Bước 2: Để hàm số đồng biến trên (p;q), tìm m để \(f'(x) \ge 0\) \(\forall x \in (p;q)\). Để hàm số nghịch biến trên (p;q), tìm m để \(f'(x) \le 0\) \(\forall x \in (p;q)\).

Cách 2: Cô lập m và xét dấu theo quy tắc:

+ \(m \ge f(x),\forall x \in (p;q) \Leftrightarrow m \ge \mathop {\max }\limits_{(p;q)} f(x)\).

+ \(m \le f(x),\forall x \in (p;q) \Leftrightarrow m \le \mathop {\max }\limits_{(p;q)} f(x)\).

2) Đối với hàm phân thức bậc nhất trên bậc nhất \(y = \frac{{ax + b}}{{cx + d}}\):

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính đạo hàm f’(x).

Bước 3: Kết luận:

- Hàm số đồng biến trên khoảng (p;q) \( \Leftrightarrow \left\{ \begin{array}{l}f'(x) > 0\\ - \frac{d}{c} \notin (p;q)\end{array} \right.\).

- Hàm số nghịch biến trên khoảng (p;q) \( \Leftrightarrow \left\{ \begin{array}{l}f'(x) < 0\\ - \frac{d}{c} \notin (p;q)\end{array} \right.\).

Ví dụ minh hoạ:

a) Tìm tất cả các giá trị thực của tham số m để hàm số \(y = {x^3} - 3{x^2} + (1 - m)x\) đồng biến trên \((2; + \infty )\).

b) Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \frac{{x + 3}}{{x + m}}\) đồng biến trên \(( - \infty ; - 6)\).

Giải:

a) Xét \(f(x) = {x^3} - 3{x^2} + (1 - m)x\) trên \((2; + \infty )\).

Tập xác định: \(D = \mathbb{R}\).

Ta có \(f'(x) = 3{x^2} - 6x + (1 - m)\).

Để f(x) đồng biến trên \((2; + \infty )\) thì \(f'(x) \ge 0,\forall x \in (2; + \infty )\)

\( \Leftrightarrow 3{x^2} - 6x + (1 - m) \ge 0,\forall x \in (2; + \infty )\)

\( \Leftrightarrow 3{x^2} - 6x + 1 \ge m,\forall x \in (2; + \infty )\)

\( \Leftrightarrow m \le \mathop {\min }\limits_{(2; + \infty )} \left( {3{x^2} - 6x + 1} \right)\).

Đặt \(g(x) = 3{x^2} - 6x + 1\); \(g'(x) = 6x - 6 = 0 \Leftrightarrow x = 1\).

Ta có bảng biến thiên:

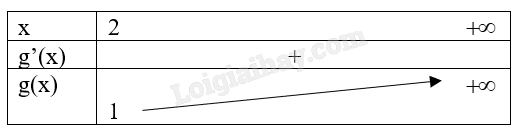
Vậy \(m \le \mathop {\min }\limits_{(2; + \infty )} \left( {3{x^2} - 6x + 1} \right) \Leftrightarrow m \le 1\).

b) Xét \(f(x) = \frac{{x + 3}}{{x + m}}\) trên \(( - \infty ; - 6)\).

Tập xác định: \(D = \mathbb{R}\backslash \{  - m\} \).

Để hàm số \(f(x) = \frac{{x + 3}}{{x + m}}\) đồng biến trên \(( - \infty ; - 6)\), ta có:

\( \Leftrightarrow \left\{ \begin{array}{l}f'(x) > 0\\ - m \notin ( - \infty ; - 6)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m - 3 > 0\\ - m \ge  - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 3\\m \le 6\end{array} \right. \Leftrightarrow 3 < m \le 6\).