Cách tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số dựa vào công thức hàm số - Toán 12

Cho hàm số \(y = f(x)\) xác định trên tập \(D\).

- Số \(M\) là giá trị lớn nhất (GTLN) của hàm số \(f\) trên \(D \).

\(⇔\left\{ \matrix{
f(x) \le M,\forall x \in D \hfill \cr
\exists \, {x_0} \in D\text{ sao cho }f({x_0}) = M \hfill \cr} \right.\)

Kí hiệu: \(M=\underset{D}{\max} f(x)\).

- Số \(m\) là giá trị nhỏ nhất (GTNN) của hàm số \(f\) trên \(D\).

\(⇔\left\{ \matrix{
f(x) \ge m,\forall x \in D \hfill \cr
\exists \, {x_0} \in D\text{ sao cho }f({x_0}) = m \hfill \cr} \right.\)

Kí hiệu: \(m=\underset{D}{\min} f(x)\).

Cho hàm số y = f(x).

Bước 1: Tìm tập xác định.

Bước 2: Tính đạo f’(x). Tìm các giá trị \({x_1},{x_2},...,{x_n} \in [a;b]\) sao cho f’(x) = 0 hoặc f’(x) không tồn tại.

Bước 3: Tính \(f\left( a \right),f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),f\left( b \right)\). Giá trị lớn nhất trong các giá trị vừa tìm là \(\mathop {\max }\limits_{[a;b]} f(x)\), giá trị nhỏ nhất trong các giá trị vừa tìm là \(\mathop {\min }\limits_{[a;b]} f(x)\).

Lưu ý: Nếu đề bài yêu cầu tìm GTLN, GTNN trên khoảng chứa \( \pm \infty \), ta cầm tìm \(\mathop {\lim }\limits_{x \to  \pm \infty } f(x)\) và so sánh.

Ví dụ minh hoạ:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) \(y = {x^3} - 8{x^2} - 12x + 1\) trên đoạn \(\left[ { - 2;9} \right]\);

b) \(y =  - 2{x^3} + 9{x^2} - 17\) trên nửa khoảng \(\left( { - \infty ;4} \right]\);

c) \(y = {x^3} - 12x + 4\) trên đoạn \(\left[ { - 6;3} \right]\);

d) \(y = 2{x^3} - {x^2} - 28x - 3\) trên đoạn \(\left[ { - 2;1} \right]\);

e) \(y =  - 3{x^3} + 4{x^2} - 5x - 17\) trên đoạn \(\left[ { - 1;2} \right]\).

Giải:

a) Xét hàm số \(y = f\left( x \right) = {x^3} - 8{x^2} - 12x + 1\) trên đoạn \(\left[ { - 2;9} \right]\).

Ta có: \(f'\left( x \right) = 3{{\rm{x}}^2} - 16{\rm{x}} - 12\)

\(f'\left( x \right) = 0 \Leftrightarrow x = 6\) hoặc \(x =  - \frac{2}{3}\).

\(f\left( { - 2} \right) =  - 15;f\left( { - \frac{2}{3}} \right) = \frac{{139}}{{27}};f\left( 6 \right) =  - 143;f\left( 9 \right) =  - 26\).

Vậy \(\mathop {\max }\limits_{\left[ { - 2;9} \right]} f\left( x \right) = f\left( { - \frac{2}{3}} \right) = \frac{{139}}{{27}},\mathop {\min }\limits_{\left[ { - 2;9} \right]} f\left( x \right) = f\left( 6 \right) = {\rm{\;}} - 143\).

b) Xét hàm số \(y = f\left( x \right) =  - 2{x^3} + 9{x^2} - 17\) trên nửa khoảng \(\left( { - \infty ;4} \right]\).

Ta có: \(f'\left( x \right) =  - 6{{\rm{x}}^2} + 18{\rm{x}}\).

\(f'\left( x \right) = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\).

Bảng biến thiên của hàm số trên nửa khoảng \(\left( { - \infty ;4} \right]\):

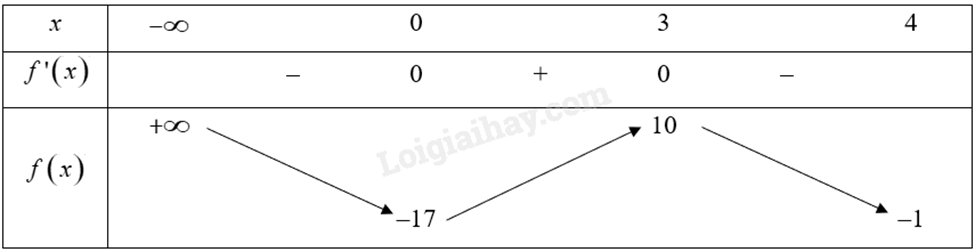
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( { - \infty ;4} \right]} f\left( x \right) = f\left( 0 \right) =  - 17\), hàm số không có giá trị lớn nhất trên nửa khoảng \(\left( { - \infty ;4} \right]\).

c) Xét hàm số \(y = f\left( x \right) = {x^3} - 12x + 4\) trên đoạn \(\left[ { - 6;3} \right]\).

Ta có: \(f'\left( x \right) = 3{{\rm{x}}^2} - 12\).

\(f'\left( x \right) = 0 \Leftrightarrow x = 2\) hoặc \(x =  - 2\).

\(f\left( { - 6} \right) = {\rm{\;}} - 140;f\left( { - 2} \right) = 20;f\left( 2 \right) =  - 12;f\left( 3 \right) =  - 5\).

Vậy \(\mathop {\max }\limits_{\left[ { - 6;3} \right]} f\left( x \right) = f\left( { - 2} \right) = 20,\mathop {\min }\limits_{\left[ { - 6;3} \right]} f\left( x \right) = f\left( { - 6} \right) =  - 140\).

d) Xét hàm số \(y = 2{x^3} - {x^2} - 28x - 3\) trên đoạn \(\left[ { - 2;1} \right]\).

Ta có: \(f'\left( x \right) = 6{{\rm{x}}^2} - 2{\rm{x}} - 28\).

\(f'\left( x \right) = 0 \Leftrightarrow x = \frac{7}{3}\) (loại) hoặc \(x =  - 2\).

\(f\left( { - 2} \right) = 33;f\left( 1 \right) =  - 30\).

Vậy \(\mathop {\max }\limits_{\left[ { - 2;1} \right]} f\left( x \right) = f\left( { - 2} \right) = 33,\mathop {\min }\limits_{\left[ { - 2;1} \right]} f\left( x \right) = f\left( 1 \right) = {\rm{\;}} - 30\).

e) Xét hàm số \(y = f\left( x \right) =  - 3{x^3} + 4{x^2} - 5x - 17\) trên đoạn \(\left[ { - 1;2} \right]\).

Ta có: \(f'\left( x \right) =  - 9{{\rm{x}}^2} + 8{\rm{x}} - 5 =  - 9{\left( {x - \frac{4}{9}} \right)^2} - \frac{{29}}{9} < 0,\forall x \in \left[ { - 1;2} \right]\).

\(f\left( { - 1} \right) =  - 5;f\left( 2 \right) =  - 35\).

Vậy \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( { - 1} \right) = - 5,\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( 2 \right) = - 35\).