Cách khảo sát sự biến thiên và vẽ đồ thị hàm số - Toán 12

Giả sử hàm số \(y = f(x)\) xác định trên \(K\).

Hàm số \(y = f(x)\) gọi là đồng biến (tăng) trên \(K\) nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1} < {x_2}\) thì \(f({x_1}) < f({x_2})\).

Hàm số \(y = f(x)\) gọi là nghịch biến (giảm) trên \(K\) nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1} < {x_2}\) thì \(f({x_1}) > f({x_2})\).

Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên \(K\).

Xét sự biến thiên của hàm số là tìm các khoảng hàm số đồng biến và các khoảng hàm số nghịch biến.

Cho hàm số y = f(x).

Bước 1: Tìm tập xác định.

Bước 2: Tính f’(x). Tìm nghiệm của f’(x) = 0 và các giá trị sao cho f’(x) không tồn tại.

Bước 3: Tính giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to  \pm \infty } f(x)\) và tìm đường tiệm cận, điểm cực trị (nếu có).

Bước 4: Tìm một số điểm đặc biệt mà đồ thị đi qua.

Bước 5: Lập bảng biến thiên và vẽ đồ thị.

Ví dụ minh hoạ:

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y =  - {x^3} + 3x + 1\).

Tập xác định: \(D = \mathbb{R}\).

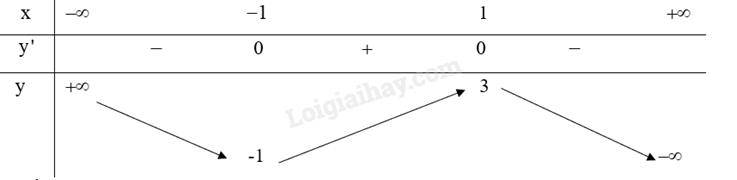
Ta có: \(y' =  - 3{x^2} + 3,y' = 0 \Leftrightarrow x =  \pm 1\).

Trên khoảng \(\left( { - 1;1} \right)\), \(y' > 0\) nên hàm số đồng biến. Trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\), \(y' < 0\) nên hàm số nghịch biến.

Hàm số đạt cực đại tại \(x = 1\), giá trị cực đại \({y_{CD}} = 3\) . Hàm số đạt cực tiểu tại \(x =  - 1\), giá trị cực tiểu \({y_{CT}} =  - 1\).

Giới hạn tại vô cực:

\(\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } \left( { - {x^3} + 3x + 1} \right) = \mathop {\lim }\limits_{x \to  - \infty } \left[ {{x^3}\left( { - 1 + \frac{3}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)} \right] =  + \infty \);

\(\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } \left( { - {x^3} + 3x + 1} \right) = \mathop {\lim }\limits_{x \to  + \infty } \left[ {{x^3}\left( { - 1 + \frac{3}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)} \right] =  - \infty \).

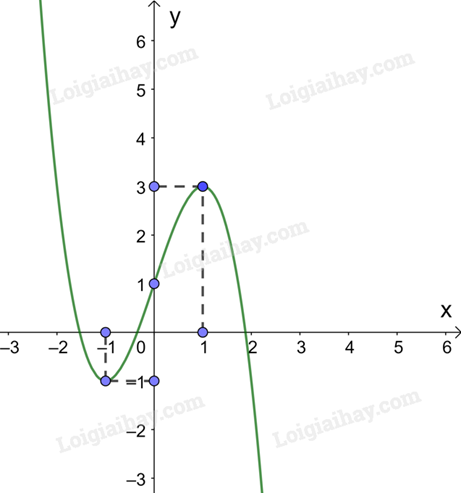
Giao điểm của đồ thị hàm số \(y =  - {x^3} + 3x + 1\) với trục tung là (0;1).

Các điểm (1; 3); \(\left( { - 1; - 1} \right)\) thuộc đồ thị hàm số \(y =  - {x^3} + 3x + 1\).

Đồ thị hàm số có tâm đối xứng là điểm (0; 1).

Bảng biến thiên:

Đồ thị:

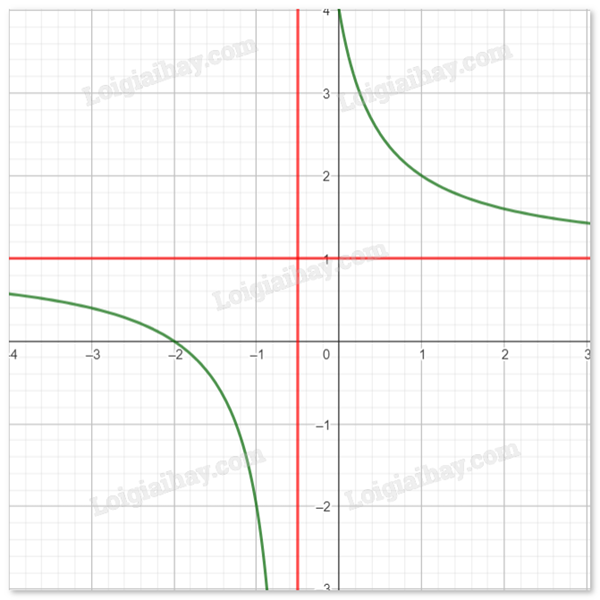
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = f(x) = \frac{{2x + 4}}{{2x + 1}}.\)

Tập xác định: \({\rm{D}} = {\rm{R}}\backslash \left\{ {\frac{{ - 1}}{2}} \right\}\).

Giới hạn, tiệm cận:

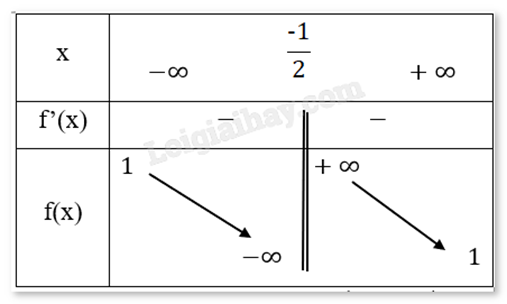
\(\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } f(x) = \mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } \frac{{2x + 4}}{{2x + 1}} = 1\); \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } f(x) = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{2x + 4}}{{2x + 1}} = 1\).

Suy ra đường thẳng \({\rm{y}} = 1\) là đường tiệm cận ngang của đồ thị hàm số đã cho.

\(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} \frac{{2x + 4}}{{2x + 1}} =  + \infty \); \(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} \frac{{2x + 4}}{{2x + 1}} =  - \infty \).

Suy ra đường thẳng \({\rm{x}} = \frac{{ - 1}}{2}\) là đường tiệm cận đứng của đồ thị hàm số đã cho.

Ta có: \(y = \frac{{ - 6}}{{{{(2x + 1)}^2}}} < 0\). Suy ra hàm số nghịch biến trên tập xác định.

Hàm số không có cực trị.

Bảng biến thiên:

Đồ thị:

c) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{ - {x^2} - 2x - 2}}{{x + 1}}\).

Tập xác định: D = R \ {-1}.

Giới hạn:

\(\mathop {\lim }\limits_{x \to  - {1^ + }} y = \mathop {\lim }\limits_{x \to  - {1^ + }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to  - {1^ + }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to  - {1^ + }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] =  - \infty \);

\(\mathop {\lim }\limits_{x \to  - {1^ - }} y = \mathop {\lim }\limits_{x \to  - {1^ - }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to  - {1^ - }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to  - {1^ - }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = \infty \).

Suy ra x = -1 là tiệm cận đứng của hàm số.

\(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to \infty } [ - (x + 1)] - 0 =  - \infty \)_;

\(\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to  - \infty } [ - (x + 1)] - 0 = \infty \)_.

Suy ra hàm số không có tiệm cận ngang.

\(\frac{{ - {x^2} - 2x - 2}}{{x + 1}} =  - x - 1 + \frac{{ - 1}}{{x + 1}}\) (Sử dụng phép chia đa thức).

Khi \(\mathop {\lim }\limits_{x \to  \pm \infty } \frac{{ - 1}}{{x + 1}} = 0\) nên \(y =  - x - 1\) là tiệm cận xiên của hàm số.

Ta có: \(y' = \frac{{ - (2x + 2)(x + 1) + \left( {{x^2} + 2x + 2} \right)}}{{{{(x + 1)}^2}}} = \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}\)_.

\(y' = 0 \Leftrightarrow  - {x^2} - 2x \Leftrightarrow  - x(x + 2) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.\)_..

Bảng biến thiên:

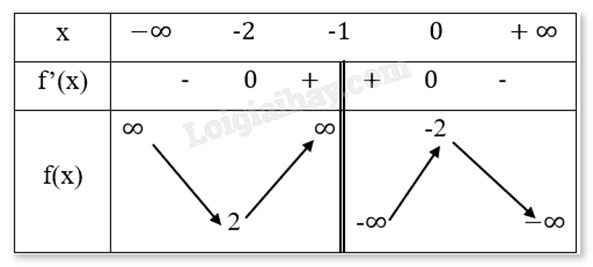
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞;-2) và (-1;0), đồng biến trên khoảng (-2;-1) và (-1;0).

Cực trị: Hàm số đạt cực tiểu tại \(x =  - 2\), \({y_{CT}} = 2\)_.

Hàm số đạt cực đại tại \(x = 0\), \({y_{CD}} =  - 2\)_.

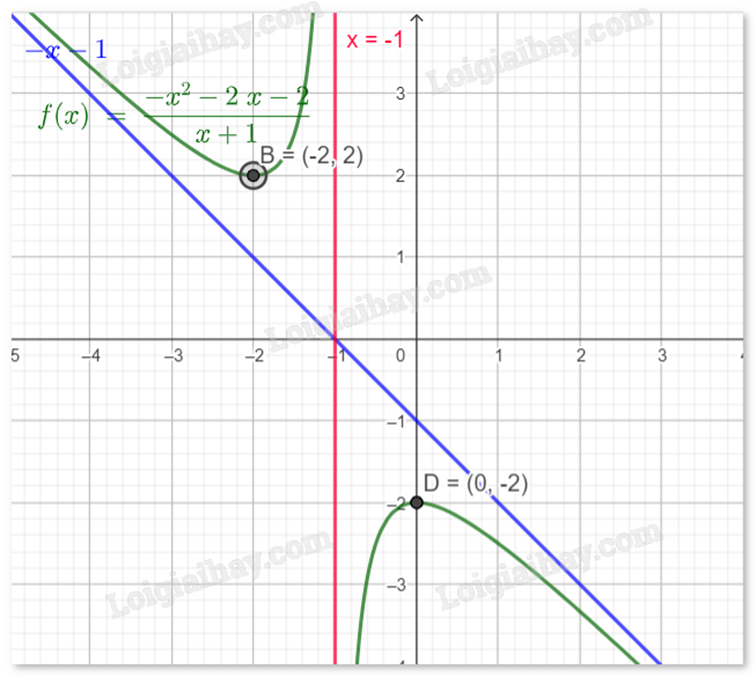
Đồ thị:

Tiệm cận đứng \({\rm{x}} =  - 1\), tiệm cận xiên \(y =  - x - 1\)_.

Giao điểm với trục Oy là \((0; - 2)\)._.